11 Asimptotične vrednosti / Asimptote
Definicija 11.1:
- Kadar je
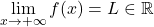 ali
ali 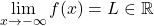 , pravimo, da je premica
, pravimo, da je premica 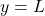 vodoravna asimptota funkcije
vodoravna asimptota funkcije  Graf funkcije
Graf funkcije  se približuje vodoravni premici
se približuje vodoravni premici 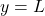 .
. - Kadar je
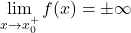 ali
ali 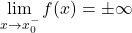 , pravimo, da je premica
, pravimo, da je premica 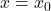 navpična asimptota funkcije
navpična asimptota funkcije  . Graf funkcije
. Graf funkcije  se približuje navpični premici
se približuje navpični premici 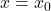 .
. - Kadar je
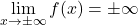
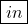
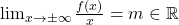
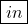
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to \pm \infty} [f(x) - mx] = q \in \mathbb{R}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-7098a387b7ffc5e5331f9745fac53ee0_l3.png) , pravimo, da je premica
, pravimo, da je premica 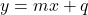 poševna asimptota funkcije
poševna asimptota funkcije  .
.
Primer 11.1: Poiščimo vse asimptote funkcije ![]() , podane s predpisom
, podane s predpisom
![]()
Najprej preverimo, ali ima funkcija vodoravne asimptote. Izračunajmo vrednost limite:
![]()
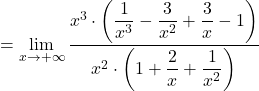
![]()
Podobno tudi dobimo, da je ![]() To pomeni, da funkcija pri
To pomeni, da funkcija pri ![]() nima vodoravnih asimptot, lahko pa ima poševne asimptote. Računajmo:
nima vodoravnih asimptot, lahko pa ima poševne asimptote. Računajmo:
![]()
![]()
![]()
![]()
![]()
Torej, premica ![]() je poševna asimptota funkcije
je poševna asimptota funkcije ![]() .
.
Dana funkcija je racionalna, ničle imenovalca so torej poli funkcije. Ker je ![]() , to pomeni, da je točka
, to pomeni, da je točka ![]() pol funkcije
pol funkcije ![]() . V tej točki izračunamo levo in desno limito in dobimo:
. V tej točki izračunamo levo in desno limito in dobimo:
![]()
![]()
Torej, premica ![]() je navpična asimptota dane funkcije.
je navpična asimptota dane funkcije.
Graf te funkcije na intervalu ![]() je na sliki 11.1.
je na sliki 11.1.
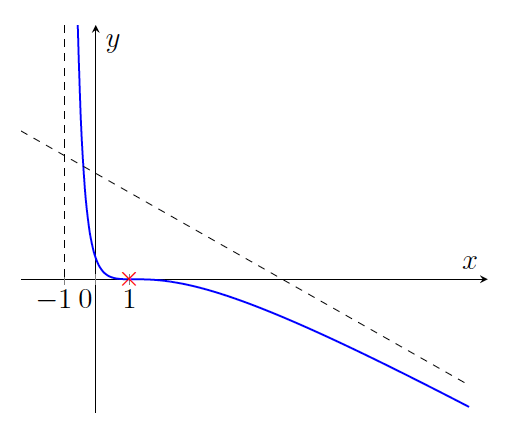
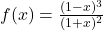 na intervalu
na intervalu 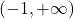 .
.