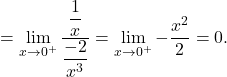20 L’Hôpitalovo pravilo
L’Hôpitalovo pravilo je recept za računanje limit funkcij z nedoločenimi izrazi z uporabo odvodov.
Prva nedoločena oblika, ki jo lahko izračunamo s tem pravilom, je oblika ![]() .
.
Izrek 20.1 [10]: Če sta ![]() in
in ![]() taki funkciji, da velja
taki funkciji, da velja
-
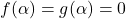
- ter obstaja taka okolica točke
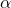 , v kateri sta
, v kateri sta  in
in  odvedljivi in za kateri velja
odvedljivi in za kateri velja  in
in 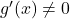 za vsak
za vsak 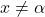 ,
, - in obstaja limita
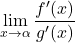 ,
,
potem obstaja tudi limita ![]() in velja
in velja ![]() .
.
Primer 20.1: Izračunajmo naslednje limite:
Podobno lahko l’Hôpitalovo pravilo uporabimo tudi za izračun limit oblike ![]() .
.
Izrek 20.2 [10]: Naj bosta funkciji ![]() in
in ![]() odvedljivi v okolici točke
odvedljivi v okolici točke ![]() in
in ![]() . Če obstaja
. Če obstaja ![]() , potem obstaja tudi limita
, potem obstaja tudi limita ![]() in obe limiti sta enaki.
in obe limiti sta enaki.
Primer 20.2: Izračunajmo naslednje limite:
Nedoločeno obliko ![]() ali
ali ![]() najprej preoblikujemo v ulomek
najprej preoblikujemo v ulomek ![]() ali
ali ![]() in potem uporabimo l’Hôpitalovo pravilo.
in potem uporabimo l’Hôpitalovo pravilo.
Primer 20.3: Izračunajmo naslednje limite:
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to 0} \frac{e^x-1}{\ln (x+1)} \stackrel{\left[\frac{0}{0}\right]}{\underset{\text{L'H}}{=}} \lim_{x \to 0} \frac{(e^x-1)'}{(\ln (x+1))'}= \lim_{x \to 0} \frac{e^x}{\dfrac{1}{x+1}} = 1.](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4aef01a4b62db1540b97fe8c4bce6b07_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to 0} \frac{2 \sin x - \sin (2x) }{x - \sin x} \stackrel{\left[\frac{0}{0}\right]}{\underset{\text{L'H}}{=}} \lim_{x \to 0} \frac{(2 \sin x - \sin (2x) )'}{(x - \sin x)'}= \lim_{x \to 0} \frac{2 \cos x - 2 \cos (2x) }{1 - \cos x} \stackrel{\left[\frac{0}{0}\right]}{\underset{\text{L'H}}{=}}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5be4f79f2634b0b4de44c97842ec2281_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to +\infty} \dfrac{\ln (\dfrac{x}{x+1})}{\ln (\dfrac{x}{x-1})}\stackrel{\left[\frac{\ln 1}{\ln 1}=\frac{\infty}{\infty}\right]}{\underset{\text{L'H}}{=}}\lim_{x \to +\infty} \dfrac{\left[\ln (\dfrac{x}{x+1})\right]'}{\left[\ln (\dfrac{x}{x-1})\right]'}=](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-c26c781a63bcdc01abf9bfeb6c883ffb_l3.png)
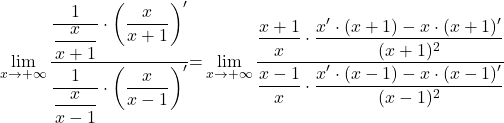
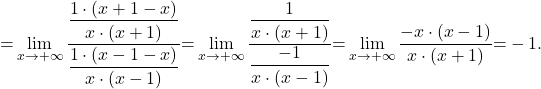
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to 0^+} \dfrac{\ln (x^2+2x)}{\ln x} \stackrel{\left[\frac{\infty}{\infty}\right]}{\underset{\text{L'H}}{=}}\lim_{x \to 0^+} \dfrac{(\ln (x^2+2x))'}{(\ln x)'}= \lim_{x \to 0^+} \dfrac{\dfrac{2x+2}{x^2+2x}}{\dfrac{1}{x}}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-7e1211a71f3c904f6c1dc8ccb1001822_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to 0^+} \dfrac{\ln (e^x-1)}{\ln x} \stackrel{\left[\frac{\infty}{\infty}\right]}{\underset{\text{L'H}}{=}}\lim_{x \to 0^+} \dfrac{(\ln (e^x-1))'}{(\ln x)'} =\lim_{x \to 0^+} \dfrac{\dfrac{e^x}{e^x - 1}}{\dfrac{1}{x}}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-546b7413bfe611b2d56560e2367ef645_l3.png)
![Rendered by QuickLaTeX.com =\displaystyle\lim_{x \to 1^+} \dfrac{\dfrac{1}{x} -1}{\ln x +(x-1)\cdot\dfrac{1}{x}} \stackrel{\left[\frac{0}{0}\right]}{\underset{\text{L'H}}{=}} \lim_{x \to 1^+} \dfrac{\left(\dfrac{1}{x} -1\right)'}{\left(\ln x +1-\dfrac{1}{x}\right)'}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-b6afb76db2fc86770666124c94a32060_l3.png)
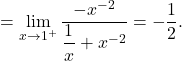
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to 0^+} (\sqrt{x} \cdot \ln x) \stackrel{\left[0\cdot(-\infty)\right]}{=}\lim_{x \to 0^+} \dfrac{\ln x}{\dfrac{1}{\sqrt{x}}}\stackrel{\left[\frac{\infty}{\infty}\right]}{\underset{\text{L'H}}{=}}\lim_{x \to 0^+} \dfrac{(\ln x)'}{(\dfrac{1}{\sqrt{x}})'}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5feb01e1512417e8d1e2daaadfd61490_l3.png)
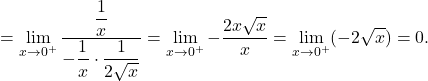
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to 0^+} (x^2 \cdot \ln x) \stackrel{\left[0\cdot(-\infty)\right]}{=} \lim_{x \to 0^+} \dfrac{\ln x}{\dfrac{1}{x^2}}\stackrel{\left[\frac{\infty}{\infty}\right]}{\underset{\text{L'H}}{=}} \lim_{x \to 0^+} \dfrac{(\ln x)'}{(\dfrac{1}{x^2})'}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-d570b49d00037c6cf1333d1787289eb0_l3.png)