22 Interaktivne naloge
Naloga 1: Izračunajte vsoto ![]() za naslednji matriki reda
za naslednji matriki reda ![]() s kompleksnimi elementi:
s kompleksnimi elementi:
![Rendered by QuickLaTeX.com \[ A=\begin{pmatrix}4+i&i&0\\ 1+i&7-3i&2-9i\\ \overline{-1-2i}& 11+3i & \overline{i} \end{pmatrix}\quad\text{in}\quad B=\begin{pmatrix}\overline{-5i}&0&\overline{1-i}\\ -(2+i)&3i&1+i\\ 1-i& -3+2i & 5+2i \end{pmatrix}. \]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-308d6d567914aefd66cf3d9cb9af7336_l3.png)
Rešitev: Najprej uredimo matriki ![]() in
in ![]() in dobimo
in dobimo
![Rendered by QuickLaTeX.com \[ A=\begin{pmatrix}4+i&i&0\\ 1+i&7-3i&2-9i\\ -1+2i& 11+3i & -i \end{pmatrix} \]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-3696c317717ae4ef2c08f972fc0af8ce_l3.png)
in
![Rendered by QuickLaTeX.com \[ B=\begin{pmatrix}5i&0&1+i\\ -2-i&3i&1+i\\ 1-i& -3+2i & 5+2i \end{pmatrix}, \]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-19e0f0f3a711a4a3bfc3cf88af60bb70_l3.png)
torej je vsota danih matrik enaka
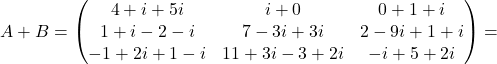
Naloga 2: Razpravljajte, za katere vrednosti parametra ![]() naslednji matriki komutatirata (torej velja
naslednji matriki komutatirata (torej velja ![]() ):
):
![]()
Rešitev: Ker je
velja ![]() natanko tedaj, ko je:
natanko tedaj, ko je:
![Rendered by QuickLaTeX.com \[ \begin{cases} \lambda+2=3\\ 3\lambda-1=2\lambda\\ -2=\lambda-3\\ 1=\lambda^2 \end{cases}. \]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-91612f9a2d9fe2f644ef5df974fc7f2c_l3.png)
Po zadnji enačbi je ![]() , ampak
, ampak ![]() ne zadošča prvi enačbi, ker je
ne zadošča prvi enačbi, ker je ![]() . Ker
. Ker ![]() zadošča vsem trem enačbam, zaključimo, da sta matriki komutativni le za
zadošča vsem trem enačbam, zaključimo, da sta matriki komutativni le za ![]() .
.
Naloga 3: Dane so matrike
![Rendered by QuickLaTeX.com \[ A=\begin{pmatrix}1&-1\\ 3&4\end{pmatrix}~\text{ , }~B=\begin{pmatrix} 1 & 0 & -1 & 3\\ 2 &-1 & 1 & 0 \end{pmatrix}~\text{ in }~C=\begin{pmatrix} 1 &2\\ 7 &3\\ 2&0\\ 0&1 \end{pmatrix}. \]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-bd188cd1901ee5065b3e4c64582b3e95_l3.png)
Poiščite, če je to mogoče, matriko ![]() .
.
Rešitev: Najprej izračunamo produkt
![Rendered by QuickLaTeX.com \[ B\cdot C=\begin{pmatrix} 1 & 0 & -1 & 3\\ 2 &-1 & 1 & 0 \end{pmatrix}\begin{pmatrix} 1 &2\\ 7 &3\\ 2&0\\ 0&1 \end{pmatrix}=\begin{pmatrix}1-2&2+3\\ 2-7+2&4-3\end{pmatrix}=\begin{pmatrix}-1&5\\ -3&1\end{pmatrix} \]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-8eca02b89f940985e5466f15764e21e0_l3.png)
in potem dobimo
![]()
Naloga 4: Izrazite neznanko ![]() iz matrične enačbe:
iz matrične enačbe:
-
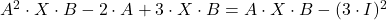
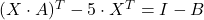
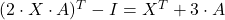
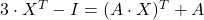 .
.
Rešitev:
-
- Uporabimo najprej lastnost transponiranja produkta matrik
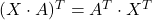 in dobimo
in dobimo
![Rendered by QuickLaTeX.com \[A^T\cdot X^T-5 \cdot X^T=I-B.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-be7c7d855a4ddd48921568d0da8d155a_l3.png)
Iz tega izpostavimo
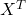 na desno in enačba postane
na desno in enačba postaneČe je matrika
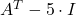 obrnljiva, dobimo
obrnljiva, dobimo![Rendered by QuickLaTeX.com \[X^T=(A^T-5 \cdot I)^{-1}\cdot (I-B),\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-b2b14bed981d342429c0f597b0fb0a72_l3.png)
ekvivalentno z
![Rendered by QuickLaTeX.com \[X=((A^T-5 \cdot I)^{-1}\cdot (I-B))^T=(I-B)^T\cdot ((A^T-5 \cdot I)^{-1})^T.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4c96c714ab21abb01d50ef1d27e92e2e_l3.png)
-
Uredimo enačbo in dobimo
![Rendered by QuickLaTeX.com \[2 \cdot A^T\cdot X^T-X^T=3 \cdot A+I\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-bb44780138eed83ed290d2bdb940c834_l3.png)
![Rendered by QuickLaTeX.com \[(2 \cdot A^T-I)\cdot X^T=3\cdot A+I.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-34240b0e7ee01308802c9db4372eab00_l3.png)
Če je matrika
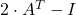 obrnljiva, dobimo
obrnljiva, dobimo![Rendered by QuickLaTeX.com \[X^T=(2\cdot A^T-I)^{-1}\cdot (3\cdot A+I)\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-3c9b5e477e1bdd9d1a9bb0e064ac04cf_l3.png)
in potem dobimo matriko
 .
. - Uredimo enačbo in dobimo
![Rendered by QuickLaTeX.com \[ 3 \cdot X^T-X^T\cdot A^T=A+I\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-714c09057bc1f75a9bd1e6dc1fa593e3_l3.png)
![Rendered by QuickLaTeX.com \[X^T(3\cdot I-A^T)=A+I.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-eaf0e97d32457f99816a226f33134f4c_l3.png)
Če je matrika
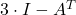 obrnljiva, dobimo
obrnljiva, dobimo![Rendered by QuickLaTeX.com \[X^T=(A+I)\cdot (3\cdot I-A^T)^{-1}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-369b992246ef8e4627d64dfe09e6d8b2_l3.png)
Naloga 5: Dana je matrika
![Rendered by QuickLaTeX.com \[ A=\begin{pmatrix}1&0&1\\ 2&-1&3\\ 1& 4& 2 \end{pmatrix}. \]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-6e98852d051c45bdc44eaa9e589e88cc_l3.png)
Če je matrika ![]() obrnljiva, poiščite njeno inverzno matriko
obrnljiva, poiščite njeno inverzno matriko ![]() .
.
Rešitev: Najprej izračunamo determinanto matrike ![]() z razvojem po prvi vrstici:
z razvojem po prvi vrstici:
![Rendered by QuickLaTeX.com \[ \det(A)=\begin{vmatrix}1&0&1\\ 2&-1&3\\ 1& 4& 2 \end{vmatrix}=-14+9=-5\neq 0, \]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-2511b2cf22780463f5c44b95cd3b310c_l3.png)
kar pomeni, da je ![]() obrnljiva matrika.
obrnljiva matrika.
Transponiranka matrike kofaktorjev je:
![Rendered by QuickLaTeX.com \[ B_A=(k_{ij})^\textup{T}=(k_{ji})=\begin{pmatrix}-14&4&1\\ -1&1&-1\\ 9& -4& -1\end{pmatrix} \]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-96849f7178cbd7a47da76bf7be3a3ec3_l3.png)
in zato je
![Rendered by QuickLaTeX.com \[ A^{-1}=\frac{1}{\det(A)}\cdot B_A=\begin{pmatrix}\dfrac{14}{5}&-\dfrac{4}{5}&-\dfrac{1}{5}\\[6pt] \dfrac{1}{5}&-\dfrac{1}{5}&\dfrac{1}{5}\\[6pt] -\dfrac{9}{5}& \dfrac{4}{5}& \dfrac{1}{5}\end{pmatrix}. \]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-fd0b8ab1469329c87646ebd92718cd07_l3.png)
Naloga 6: Rešite naslednji sistem linearnih enačb:
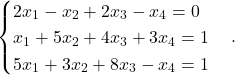
Rešitev:
Dobimo ![]() in rešitev je 1-parametrična, ker je
in rešitev je 1-parametrična, ker je ![]() . Potem je pripadajoči sistem
. Potem je pripadajoči sistem
![Rendered by QuickLaTeX.com \[\begin{cases} x_1 + 5x_2 + 4x_3 + 3x_4 = 1 \\ -11x_2 - 6x_3 - 7x_4 = -2 \\ -2 x_4 = 0 \end{cases}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-ad08be5c564ad80dff341cab4985bdcf_l3.png)
Torej, ![]() in druga enačba zadnjega sistema postane
in druga enačba zadnjega sistema postane ![]() , kjer lahko izberemo
, kjer lahko izberemo ![]() kot parameter (
kot parameter (![]() je poljubno realno število). Sledi, da je
je poljubno realno število). Sledi, da je ![]() oziroma
oziroma ![]() . Potem iz prve enačbe dobimo
. Potem iz prve enačbe dobimo ![]() . Sklepamo, da je sistem neskončno rešljiv.
. Sklepamo, da je sistem neskončno rešljiv.
Naloga 7: Izračunajte razdaljo med točko ![]() in premico
in premico 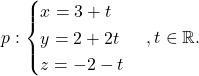
Rešitev: Ker koordinate dane točke ne zadoščajo enačbi premice ![]() (ne obstaja nobena vrednost parametra
(ne obstaja nobena vrednost parametra ![]() , tako da je
, tako da je ![]() ), sklepamo, da točka
), sklepamo, da točka ![]() ni na premici
ni na premici ![]() in je torej razdalja med točko
in je torej razdalja med točko ![]() in premico različna od
in premico različna od ![]() .
.
Na podlagi formule za izračun te razdalje potrebujemo naslednje elemente:
- smerni vektor premice
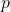 , ki je vektor
, ki je vektor 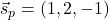 ;
; - krajevni vektor točke
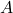 , ki je vektor
, ki je vektor 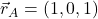 ;
; - krajevni vektor točke
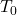 , ki pripada premici
, ki pripada premici 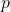 , je vektor
, je vektor 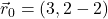 .
.
Dobimo:
![]()
ker je
![Rendered by QuickLaTeX.com \[(-2,-2,3)\times (1,2,-1)=\begin{vmatrix} \bar{i}&\bar{j}&\bar{k}\\ -2& -2& 3\\ 1& 2& -1\end{vmatrix}=\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-3b02594e71f249578428c8a5912783ed_l3.png)
in
![]()
Naloga 8: Naj bosta dani premici 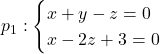 in
in ![]() , ki gre skozi točki
, ki gre skozi točki ![]() in
in ![]() .
.
- Ali sta premici
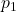 in
in 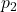 vzporedni?
vzporedni? - Izračunajte razdaljo med
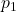 in
in 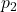 .
. - Zapišite enačbo ravnine
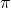 , ki vsebuje točko
, ki vsebuje točko 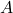 in je pravokotna na premico
in je pravokotna na premico 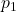 .
. - Zapišite enačbo ravnine
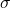 , določene z vektorjema
, določene z vektorjema 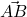 in
in 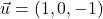 .
. - Katera premica je presečnica ravnin
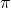 in
in 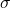 ?
?
Rešitev:
- Dve premici sta vzporedni, če sta njuna smerna vektorja vzporedna. Zato moramo najprej določiti smerna vektorja premic
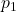 in
in 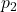 . Zapišemo parametrično obliko enačbe premice
. Zapišemo parametrično obliko enačbe premice 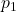 . Nato rešimo sistem, ki opisuje enačbo premice
. Nato rešimo sistem, ki opisuje enačbo premice 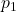 , pri čemer kot parameter vzamemo
, pri čemer kot parameter vzamemo  , tj.
, tj. 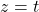 . Iz druge enačbe dobimo
. Iz druge enačbe dobimo 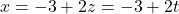 , ki ga vstavimo v prvo enačbo. Sledi, da je
, ki ga vstavimo v prvo enačbo. Sledi, da je 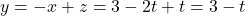 . Enačba premice
. Enačba premice 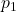 ima parametrično obliko
ima parametrično obliko
![Rendered by QuickLaTeX.com \[p_1: \begin{cases} x=-3+2t\\ y=3-t\\ z=t\end{cases}, t\in\mathbb{R},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-9b94c5419f11779074574f40b687a27a_l3.png)
ki pokaže, da je smerni vektor
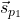 enak
enak 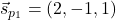 . Premica
. Premica 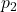 skozi točki
skozi točki 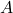 in
in 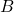 ima smerni vektor
ima smerni vektor 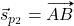 .
.Opazimo, da je
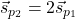 , torej sta vektorja linearno odvisna in tudi vzporedna, kar pomeni, da sta premici
, torej sta vektorja linearno odvisna in tudi vzporedna, kar pomeni, da sta premici 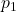 in
in 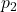 vzporedni.
vzporedni. - Ker sta premici
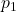 in
in 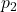 vzporedni, je razdalja med njima enaka razdalji med točko
vzporedni, je razdalja med njima enaka razdalji med točko 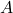 in premico
in premico 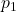 :
:
![Rendered by QuickLaTeX.com \[d(p_1,p_2)=d(A, p_1)=\displaystyle\frac{\norm{(\vec{r}_A-\vec{r}_0)\times \vec{s}_{p_1}}}{\norm{\vec{s}_{p_1}}},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-b693d17947357d7ff77c0f24b3de2019_l3.png)
kjer so
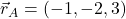 ,
, 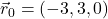 (krajevni vektor točke
(krajevni vektor točke 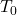 na premici
na premici 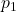 ) ter
) ter 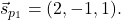 Izračunamo
Izračunamo![Rendered by QuickLaTeX.com \[(\vec{r}_A-\vec{r}_0)\times \vec{s}_{p_1}=(2, -5, 3)\times (2,-1,1).\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-b108a68c56e173ba21437bbcdfe568b0_l3.png)
Torej
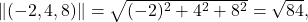
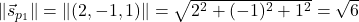 . Na koncu dobimo, da je
. Na koncu dobimo, da je ![Rendered by QuickLaTeX.com \[d(p_1,p_2)=\sqrt{\displaystyle\frac{84}{6}}=\sqrt{14}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-c7170a76719e9aa5513d921ed832e2a8_l3.png)
- Ravnina
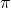 je pravokotna na premico
je pravokotna na premico 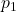 , torej je njen normalni vektor enak smernemu vektorju premice
, torej je njen normalni vektor enak smernemu vektorju premice 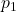 , tj.
, tj. 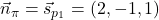 . Splošna oblika enačbe ravnine je
. Splošna oblika enačbe ravnine je 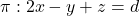 . Ker točka
. Ker točka 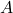 pripada ravnini
pripada ravnini 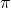 , njene koordinate zadoščajo enačbi ravnine:
, njene koordinate zadoščajo enačbi ravnine:
Splošna oblika enačbe ravnine je torej
![Rendered by QuickLaTeX.com \[\pi: 2x-y+z=3.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-f2193726d864b1ed58385bff99537fda_l3.png)
- Normalni vektor
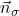 ravnine
ravnine 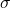 , ki je določena z vektorjema
, ki je določena z vektorjema 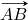 in
in 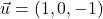 , je pravokoten na oba vektorja,
, je pravokoten na oba vektorja, 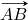 in
in 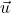 , in je torej
, in je torej
![Rendered by QuickLaTeX.com \[\vec{n}_{\sigma}=\vv{AB}\times \vec{u}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4c5ef45955ae7d2b0ab1b547806dd150_l3.png)
Splošna oblika enačbe ravnine
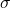 je
je 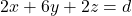 , in ker ravnina
, in ker ravnina 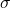 vsebuje točko
vsebuje točko 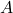 , dobimo, da je
, dobimo, da je 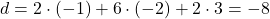 .
.
Enačba ravnine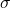 ima obliko:
ima obliko:![Rendered by QuickLaTeX.com \[\sigma: 2x+6y+2z=-8 \Leftrightarrow x+3y+z=-4.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-74576e3bd78f05a90ff6407a1cefff89_l3.png)
- Presečišče danih ravnin je premica
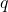 , ki ima enačbo:
, ki ima enačbo:
![Rendered by QuickLaTeX.com \[q=\pi\cap \sigma: \begin{cases} 2x-y+z=3\\ x+3y+z=-4.\end{cases}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-e88c97e968a22a2c015f5dd2b1cb7187_l3.png)
Če odštejemo drugo enačbo od prve, dobimo
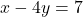 . Vzamemo
. Vzamemo 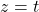 (poljubno realno število) in potem sledi, da je
(poljubno realno število) in potem sledi, da jePremica
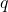 ima enačbo
ima enačbo![Rendered by QuickLaTeX.com \[q: \begin{cases} x=7+4t\\ y=t\\ z=-11-7t\end{cases}, t\in\mathbb{R}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-00190d31579ceaa08b4aec3663890da0_l3.png)
Naloga 9: Poiščite razdaljo med premico 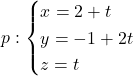 ,
, ![]() in ravnino
in ravnino ![]() .
.
Rešitev:
Če se premica in ravnina sekata, potem je razdalja med njima enaka ![]() , sicer pa pomeni, da sta vzporedni. V tem primeru je razdalja med njima enaka razdalji od katerekoli točke na premici do dane ravnine.
, sicer pa pomeni, da sta vzporedni. V tem primeru je razdalja med njima enaka razdalji od katerekoli točke na premici do dane ravnine.
Najprej preverimo, ali se premica in ravnina sekata. To se zgodi, ko obstaja neko realno število ![]() , tako da parametri
, tako da parametri ![]() ,
, ![]() in
in ![]() , ki določajo enačbo premice
, ki določajo enačbo premice ![]() , zadoščajo enačbi ravnine
, zadoščajo enačbi ravnine ![]() :
:
![]() , kar pomeni
, kar pomeni ![]() . Zaradi dobljenega protislovja sklepamo, da sta ravnini vzporedni. Do istega sklepa bi lahko prišli z izračunom skalarnega produkta med smernim vektorjem premice
. Zaradi dobljenega protislovja sklepamo, da sta ravnini vzporedni. Do istega sklepa bi lahko prišli z izračunom skalarnega produkta med smernim vektorjem premice ![]() in normalnim vektorjem ravnine
in normalnim vektorjem ravnine ![]() . Prav zares, ker sta smerni vektor
. Prav zares, ker sta smerni vektor ![]() in normalni vektor
in normalni vektor ![]() ,
,
To pomeni, da sta vektorja ![]() in
in ![]() pravokotna, torej sta premica in ravnina vzporedni.
pravokotna, torej sta premica in ravnina vzporedni.
Upoštevamo točko ![]() na ravnini in točko
na ravnini in točko ![]() na premici, torej imamo
na premici, torej imamo ![]() in
in ![]() . Razdalja med premico in ravnino bo
. Razdalja med premico in ravnino bo
![]()
Naloga 10: Na premici 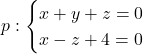 poiščite točko, ki je enako oddaljena od točk
poiščite točko, ki je enako oddaljena od točk ![]() in
in ![]() .
.
Rešitev: Parametrična oblika enačbe dane premice je 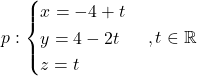 . Poiskati moramo točko
. Poiskati moramo točko ![]() na premici, ki je enako oddaljena od točk
na premici, ki je enako oddaljena od točk ![]() in
in ![]() , torej tako, da je
, torej tako, da je ![]() . Dobimo enakost
. Dobimo enakost
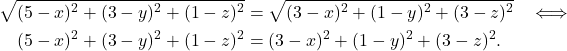
Ker točka ![]() leži na dani premici
leži na dani premici ![]() , vemo, da velja
, vemo, da velja ![]() ,
, ![]() ter
ter ![]() . Zato prejšnja enakost postane
. Zato prejšnja enakost postane
![]()
z rešitvijo ![]() .
.
Naloga 11: Določite vrednosti ![]() in
in ![]() tako, da bo funkcija
tako, da bo funkcija ![]() , podana s predpisom
, podana s predpisom
![Rendered by QuickLaTeX.com \[g(x) = \begin{cases} ax+2b,&\textup{če je x }\leq 0, \\ x^2+3a -b, &\textup{če je }0< x\leq 2,\\ 3x-5,&\textup{če je }x>2, \end{cases}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5fc95d6da748038fab6def5cc6308376_l3.png)
zvezna na ![]() .
.
Rešitev: V točki ![]() imamo
imamo
Torej,
![]()
V točki ![]() imamo
imamo ![]() in
in
![]()
Še več,
![]()
Torej, ![]() . Ob
. Ob ![]() in
in ![]() sledi, da sta
sledi, da sta
![]()
Naloga 12: Pogovorite se o zveznosti funkcije ![]() .
.
Rešitev: Domena ![]() funkcije
funkcije ![]() je interval:
je interval:
Na vseh točkah odprtega intervala ![]() je funkcija
je funkcija ![]() zvezna. In potem,
zvezna. In potem,
lahko sklepamo, da je funkcija ![]() zvezna na zaprtem intervalu
zvezna na zaprtem intervalu ![]() .
.
Naloga 13: Izračunajte limito ![]() .
.
Rešitev: Dana limita je v obliki:
Uredimo limito tako, da jo zapišemo v poenostavljeni obliki:
![]()
Torej,
![]()
![]()
Naloga 14: Naj bo funkcija ![]() podana z grafom:
podana z grafom:
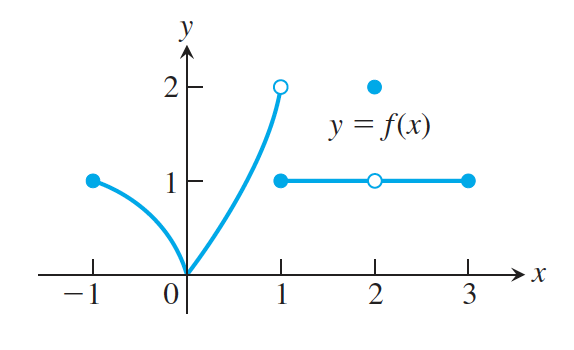
Katere trditve o funkciji ![]() so pravilne in katere so napačne?
so pravilne in katere so napačne?
Rešitev:
Naloga 15: Naj bo funkcija ![]() podana s predpisom
podana s predpisom ![]() .
.
Izračunajte limite:
Rešitev:
Naloga 16: Izračunajte odvod podane funkcije ![]() .
.
Rešitev:
Naloga 17: Podana je tabela vrednosti funkcij ![]() in
in ![]() ter njunih odvodov.
ter njunih odvodov.
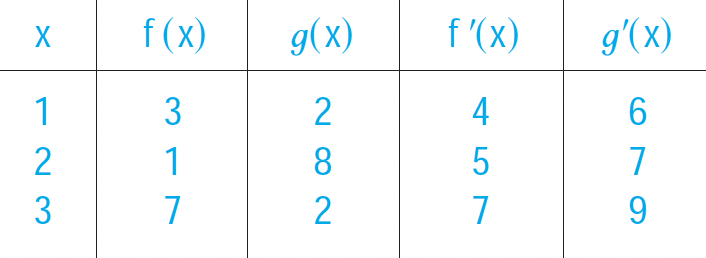
Če je ![]() ,
, ![]() in
in ![]() , poiščite naslednje vrednosti:
, poiščite naslednje vrednosti:
Rešitev:
Naloga 18: Izračunajte petdeseti odvod funkcije ![]() , podane s predpisom
, podane s predpisom
![]()
Rešitev: Izračunamo prvi odvod funkcije ![]() .
.
Zdaj izračunamo drugi odvod funkcije ![]() :
:
![]()
Torej,
Zdaj izračunamo tretji odvod funkcije ![]() :
:
![]() . Nadaljujemo in dobimo četrti odvod
. Nadaljujemo in dobimo četrti odvod
![]()
Torej, sklepamo, da je
Naloga 19: Poiščite enačbo tangente na krivuljo
![]()
v točki ![]() .
.
Rešitev: Izračunamo prvi odvod:
![]()
Sledi, da je ![]() . Torej, enačba tangente v točki
. Torej, enačba tangente v točki ![]() je
je
Naloga 20: Poiščite enačbo tangente na krivuljo
![]()
v točki ![]() .
.
Rešitev: Izračunamo prvi odvod:
Naklonski koeficient tangente je:
Torej, enačba tangente v točki ![]() je
je
Naloga 21: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]() na intervalu
na intervalu ![]() .
.
Rešitev:
- Dana funkcija je definirana tam, kjer je imenovalec različen od
 . Torej
. Torej 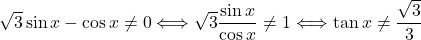 oziroma
oziroma 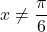 in
in 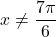 . Dobimo, da je domena
. Dobimo, da je domena
- Ničle funkcije so ničle števca. Ker je
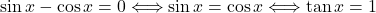 na
na ![Rendered by QuickLaTeX.com [0, 2\pi]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-ab5ce0577e8cf8aeb6bfb6e0c0488382_l3.png) , za
, za
sklepamo, da sta ničli funkcije
- Funkcija ima dva pola v točki
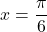 in
in 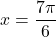 , kjer ima tudi navpični asimptoti. Nima pa ne vodoravnih ne poševnih asimptot.
, kjer ima tudi navpični asimptoti. Nima pa ne vodoravnih ne poševnih asimptot.
Izračunamo enostranske limite v dveh polih:
- Poiščemo stacionarne točke oziroma ničle prvega odvoda:
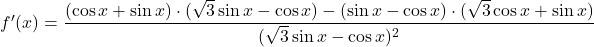
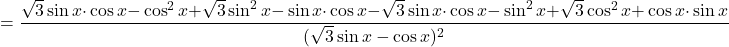
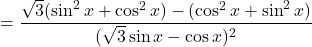
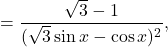
saj je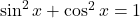 .
.
Ker je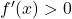 za vsak
za vsak  v domeni, sledi, da je funkcija
v domeni, sledi, da je funkcija  naraščajoča in torej nima ekstremov.
naraščajoča in torej nima ekstremov. - V naslednji tabeli bomo povzeli vse podatke, ki smo jih pridobili v prejšnjih točkah.
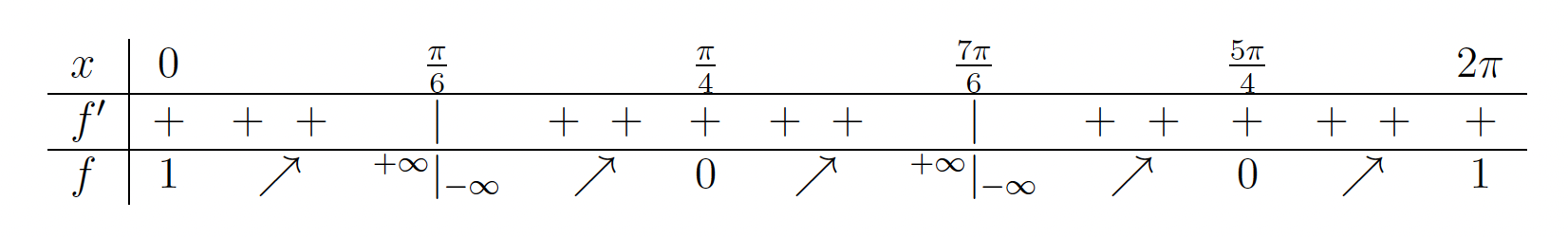
- Zdaj skiciramo graf funkcije
 (slika 22.1).
(slika 22.1).
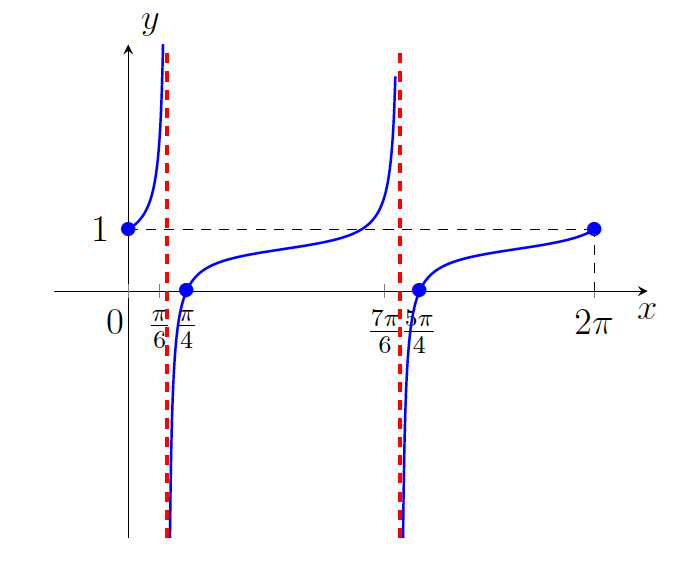
 na intervalu
na intervalu ![Rendered by QuickLaTeX.com [0, 2\pi]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-ab5ce0577e8cf8aeb6bfb6e0c0488382_l3.png) .
.Naloga 22: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]()
Rešitev:
- Logaritemska funkcija ter korenska funkcija s sodim korenskim eksponentom sta definirani za
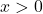 , zato je domena funkcije
, zato je domena funkcije  enaka
enaka 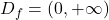 .
. - Ničle funkcije so ničle števca, torej je
- Funkcija ima pol v ničli imenovalca oziroma v točki
 . Torej je premica
. Torej je premica  navpična asimptota in desna limita v točki
navpična asimptota in desna limita v točki  je
je
![Rendered by QuickLaTeX.com \[\lim_{x \to 0^+} f(x)= \lim_{x \to 0^+} \dfrac{\ln x}{\sqrt{x}}\stackrel{[\frac{-\infty}{0^+}]}{=} \lim_{x \to 0^+} \left(\ln x\cdot \dfrac{1}{\sqrt x}\right)=(-\infty)\cdot (+\infty)=-\infty.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4214cc2224843cd0b334d983b87c7451_l3.png)
- Poiščimo vse druge eventualne asimptote. Izračunamo limito dane funkcije, ko gre
 proti
proti 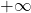 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} f(x)= \lim_{x \to +\infty} \dfrac{\ln x}{\sqrt{x}}\stackrel{[\frac{\infty}{\infty}]}{\underset{\text{L'H}}{=}}\lim_{x \to +\infty} \dfrac{\dfrac{1}{x}}{\dfrac{1}{2\sqrt x}}=\lim_{x \to +\infty} \dfrac{2\sqrt x}{x}=\lim_{x \to +\infty} \dfrac{2}{\sqrt x}=0^+,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-99dd0b8a00af929d2327e2b0bff45d22_l3.png)
kar pomeni, da je premica
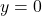 vodoravna asimptota pri
vodoravna asimptota pri 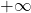 . Zato funkcija nima poševnih asimptot.
. Zato funkcija nima poševnih asimptot. - Stacionarne točke so ničle prvega odvoda:
![Rendered by QuickLaTeX.com \[f'(x) =\dfrac{(\ln x)'\cdot \sqrt{x}-\ln x\cdot (\sqrt{x})'}{(\sqrt{x})^2}=\dfrac{\dfrac{1}{x}\cdot \sqrt x-\dfrac{\ln x}{2\sqrt{x}}}{x}=\dfrac{2-\ln x}{2x\cdot \sqrt x}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-7f81fea676021181fdb25db70433be93_l3.png)
Torej,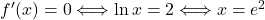
Preučimo sedaj predznak prvega odvoda funkcije . Ker je imenovalec prvega odvoda funkcije
. Ker je imenovalec prvega odvoda funkcije  vedno pozitiven, je predznak odvoda podan s predznakom števca. Dobimo
vedno pozitiven, je predznak odvoda podan s predznakom števca. Dobimo 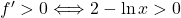 natanko tedaj, ko je
natanko tedaj, ko je 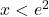 , sicer pa je
, sicer pa je 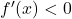 . Poleg tega sledi, da je točka
. Poleg tega sledi, da je točka 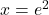 lokalni maksimum dane funkcije.
lokalni maksimum dane funkcije.
Izračunamo še drugi odvod funkcije in dobimo:
in dobimo:
![Rendered by QuickLaTeX.com \[f''(x)=&\left( \dfrac{2-\ln x}{2x\cdot \sqrt x}\right)'=\dfrac{(2-\ln x)'\cdot 2x\cdot \sqrt x-(2-\ln x)\cdot (2x^{3/2})'}{4x^3}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-a646503c771aa7a3e3c22d266e447d6a_l3.png)
![Rendered by QuickLaTeX.com \[=\dfrac{-\dfrac{1}{x}\cdot 2x\cdot \sqrt x - (2-\ln x)\cdot 2\cdot \dfrac{3}{2}\sqrt x}{4x^3} =\dfrac{-2\sqrt x-6\sqrt x+3\sqrt x\cdot \ln x}{4x^3}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-bf074e910f2f762e69fe0a20df286f83_l3.png)
![Rendered by QuickLaTeX.com \[=\dfrac{-8\sqrt x+3\sqrt x\cdot \ln x}{4x^2\cdot\sqrt x\cdot \sqrt x}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-9a50f66104372496e4b92eed665e91a1_l3.png)
![Rendered by QuickLaTeX.com \[=\dfrac{-8+3\ln x}{4x^2\cdot \sqrt x}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-a564edd240871d5b99658474ba405f05_l3.png)
Iz tega sledi, da je , ko je
, ko je 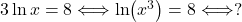
To pomeni, da je točka
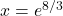 prevoj funkcije
prevoj funkcije  .
. - V naslednji tabeli bomo povzeli vse podatke, ki smo jih pridobili v prejšnjih točkah.
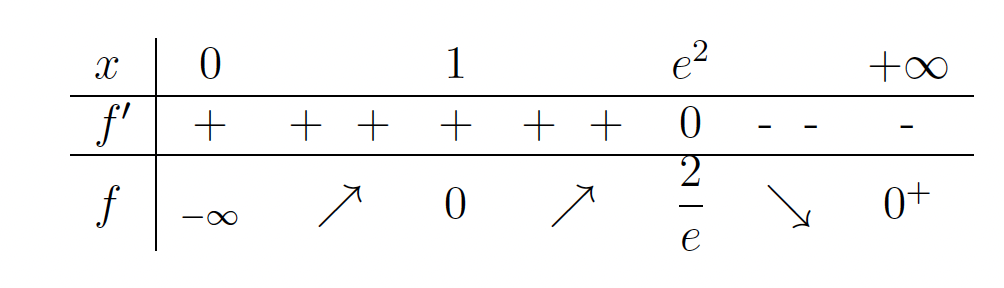
- Graf funkcije je na sliki 22.2.
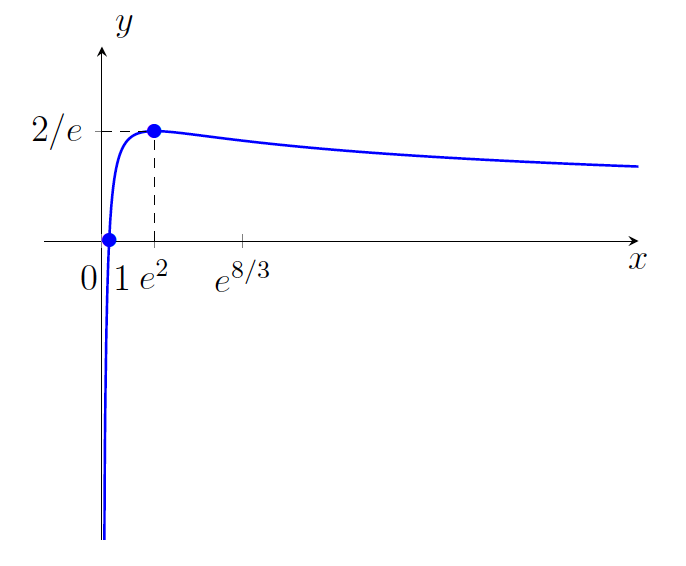
 .
.
Funkcija je konveksna na intervalu ![]() ter konkavna na intervalu
ter konkavna na intervalu ![]() .
.