21 Naloge s celotnim postopkom reševanja
Naloga 1: Izračunajte naslednjo limito: 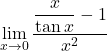 .
.
Rešitev: Ker je ![]() , je dana limita v nedoločeni obliki
, je dana limita v nedoločeni obliki ![]() , zato uporabimo l’Hôpitalovo pravilo.
, zato uporabimo l’Hôpitalovo pravilo.
![Rendered by QuickLaTeX.com \begin{align*} \lim_{x \to 0} \frac{\dfrac{x}{\tan x} - 1}{x^2} &=\lim_{x \to 0} \dfrac{x - \tan x}{x^2 \cdot \tan x} \stackrel{\left[\frac{0}{0}\right]}{\underset{\text{L'H}}{=}} \lim_{x \to 0} \dfrac{1 - \dfrac{1}{\cos^2 x}}{2x \cdot \tan x + x^2 \cdot \dfrac{1}{\cos^2 x}}=\\ &=\lim_{x \to 0} \dfrac{ \dfrac{\cos^2 x - 1}{\cos^2 x}}{\dfrac{2x \cdot \dfrac{\sin x}{\cos x} \cdot \cos^2 x + x^2}{\cos^2 x}}=\lim_{x \to 0} \dfrac{-\sin^2 x}{2x \cdot \sin x \cdot \cos x + x^2}\\ &=\lim_{x \to 0} \dfrac{x^2 \cdot \left(-\boxed{\dfrac{\sin^2 x}{x^2}}^{\nearrow 1}\right)}{x^2\cdot (2 \cdot \boxed{\dfrac{\sin x}{x}}_{\searrow 1} \cdot \cos x + 1)} = \\ &=- \dfrac{1}{3}. \end{align*}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-a23302a6e40883ff74588d862e2143e9_l3.png)
Naloga 2: Izračunajte limito ![]() .
.
Rešitev: Dana limita je v nedoločeni obliki ![]() in obe funkciji, v števcu in imenovalcu, sta odvedljivi, torej lahko uporabimo l’Hôpitalovo pravilo in dobimo:
in obe funkciji, v števcu in imenovalcu, sta odvedljivi, torej lahko uporabimo l’Hôpitalovo pravilo in dobimo:
![]()
Naloga 3: Izračunajte limito ![]() .
.
Rešitev: Ker je dana limita v nedoločeni obliki ![]() in sta oba funkciji, v števcu in imenovalcu, odvedljivi, lahko uporabimo l’Hôpitalovo pravilo. Izračunamo:
in sta oba funkciji, v števcu in imenovalcu, odvedljivi, lahko uporabimo l’Hôpitalovo pravilo. Izračunamo:
![Rendered by QuickLaTeX.com \[\lim_{x \to 1} \dfrac{x-1}{\ln x - \sin (\pi x)} \stackrel{\left[\frac{0}{0}\right]}{\underset{\text{L'H}}{=}}\lim_{x \to 1} \dfrac{1}{\dfrac{1}{x} - \pi \cos (\pi x)} = \dfrac{1}{1+\pi},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5b239500fee850d27f4c8fbcd9bd0946_l3.png)
saj je ![]() .
.
Naloga 4: Izračunajte limito ![]() , kjer sta
, kjer sta ![]() in
in ![]() dve naravni števili.
dve naravni števili.
Rešitev: Spet imamo nedoločeno obliko ![]() in uporabimo l’Hôpitalovo pravilo. Izračunamo:
in uporabimo l’Hôpitalovo pravilo. Izračunamo:
![]()
Naloga 5: Izračunajte limito ![]() .
.
Rešitev: Tokrat je dana limita v nedoločeni obliki ![]() , zato jo najprej preoblikujemo v en ulomek in potem uporabimo l’Hôpitalovo pravilo. Izračunamo:
, zato jo najprej preoblikujemo v en ulomek in potem uporabimo l’Hôpitalovo pravilo. Izračunamo:
![]()
Naloga 6: Izračunajte limito ![]() .
.
Rešitev: Dana limita je v nedoločeni obliki ![]() . Preoblikujemo jo v obliko
. Preoblikujemo jo v obliko ![]() . Potem po l’Hôpitalovem pravilu dobimo:
. Potem po l’Hôpitalovem pravilu dobimo:
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to 0^+} (\sin x \cdot \ln x) = \Lim_{x \to 0^+} \dfrac{\ln x}{\dfrac{1}{\sin x}} \stackrel{\left[\frac{0}{0}\right]}{\underset{\text{L'H}}{=}} \lim_{x \to 0^+} \dfrac{\dfrac{1}{x}}{\dfrac{-\cos x}{\sin^2 x}}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-fc9bbc5fe23712f92a049decefbd9222_l3.png)
![]()
Naloga 7: Izračunajte limito ![]() .
.
Rešitev: Če dvakrat uporabimo l’Hôpitalovo pravilo, dobimo:
![]()
Naloga 8: Izračunajte limito ![]() .
.
Rešitev: Ob pomoči L’Hôpitalovega pravila, ki smo ga uporabili večkrat, izračunamo:
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to -\infty} \dfrac{x^2\cdot \ln (x+1)+1}{x^2\cdot \ln x+2} \stackrel{\left[\frac{\infty}{\infty}\right]}{\underset{\text{L'H}}{=}} \lim_{x \to -\infty} \dfrac{2x\cdot \ln (x+1)+\dfrac{x^2}{x+1}}{2x\cdot \ln x+x^2\cdot \dfrac{1}{x}}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-a050af69a7e9d377ae1142e06618b097_l3.png)
![Rendered by QuickLaTeX.com =\displaystyle \lim_{x \to -\infty} \dfrac{x\cdot\left[ 2\ln (x+1)+\dfrac{x}{x+1}\right]}{x\cdot (2\ln x+1)}= \lim_{x \to -\infty} \dfrac{2\ln (x+1)+\dfrac{x}{x+1}}{2\ln x+1} \stackrel{\left[\frac{\infty}{\infty}\right]}{\underset{\text{L'H}}{=}}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5995ee14433fcb1c1fe0d3dae5274727_l3.png)
![Rendered by QuickLaTeX.com =\displaystyle\lim_{x \to -\infty} \dfrac{\dfrac{2}{x+1}+\dfrac{1\cdot (x+1)-x\cdot 1}{(x+1)^2}}{\dfrac{2}{x}}=\lim_{x \to -\infty} \dfrac{\dfrac{2\cdot (x+1)+1}{(x+1)^2}}{\dfrac{2}{x}}=\lim_{x \to -\infty} \dfrac{x\cdot(2x+3)}{2\cdot (x+1)^2} \stackrel{\left[\frac{\infty}{\infty}\right]}{\underset{\text{L'H}}{=}}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-46e72f005b324aa0ad805f715bdb6929_l3.png)
![]()
Naloga 9: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]() .
.
Rešitev:
- Dana funkcija je racionalna funkcija, ki je definirana tam, kjer je njen imenovalec, tj.
 , različen od
, različen od  , zato je njena domena
, zato je njena domena 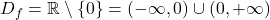 .
. - Ničle funkcije so rešitve enačbe
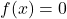 . Racionalna funkcija je enaka
. Racionalna funkcija je enaka  , ko je njen števec enak
, ko je njen števec enak  , torej ko je
, torej ko je 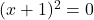 oziroma
oziroma 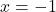 . Poli so ničle imenovalca; v tem primeru je točka
. Poli so ničle imenovalca; v tem primeru je točka  pol funkcije in zato je premica
pol funkcije in zato je premica  navpična asimptota dane funkcije.
navpična asimptota dane funkcije. - Poiščimo druge eventualne asimptote.
I) Najprej izračunamo limite funkcije, ko gre proti
proti 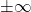 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} -\dfrac{(x+1)^2}{x}= \lim_{x \to +\infty} -\dfrac{x^2+2x+1}{x}=-\infty,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-50044154347e90707c6d64f17d892f3c_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} -\dfrac{(x+1)^2}{x}= \lim_{x \to -\infty} -\dfrac{x^2+2x+1}{x}=+\infty.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-f5d26c678513873de425c33804894608_l3.png)
Funkcija torej nima vodoravnih asimptot.
II) Preverimo, ali ima funkcija poševne asimptote.
![Rendered by QuickLaTeX.com \[\lim_{x \to \pm\infty} \dfrac{f(x)}{x}=\lim_{x \to \pm\infty} -\dfrac{(x+1)^2}{x^2}=-1=m\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-8a11879953afa490fde7f61cb46465a5_l3.png)
(števec in imenovalec sta polinoma iste stopnje in oba imata vodilni koeficient enak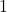 ).
).
Zdaj izračunamo drugo limito:
![Rendered by QuickLaTeX.com \[\lim_{x \to \pm\infty} [f(x)-mx]{=}\Lim_{x \to \pm\infty} \left(-\dfrac{x^2+2x+1}{x}+x\right){=}\lim_{x \to \pm\infty} \dfrac{-x^2{-}2x{-}1{+}x^2}{x}{=}-2{=}q,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-aab8cd22230fbf0fafdbb952daed9acf_l3.png)
kar pomeni, da je premica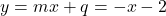 poševna asimptota naše funkcije.
poševna asimptota naše funkcije.
III) Navpična asimptota je premica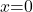 . Izračunamo še enostranski limiti v točki
. Izračunamo še enostranski limiti v točki  :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to 0^+} f(x) &= \lim_{x \to 0^+} -\dfrac{(x+1)^2}{x}=-\dfrac{1}{0^+}=-\infty,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-304ee539a8194482764a928d58ca9678_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x \to 0^-} f(x) &= \lim_{x \to 0^-} -\dfrac{(x+1)^2}{x}= -\dfrac{1}{0^-}=+\infty.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-82af30ee6438cc30065db0ae943944b8_l3.png)
- Zdaj poiščemo stacionarne točke, torej ničle prvega odvoda. Ta ima obliko
![Rendered by QuickLaTeX.com \[f'(x) = \left(-\dfrac{x^2+2x+1}{x}\right)'=-\dfrac{(2x+2)\cdot x-(x^2+2x+1)\cdot 1}{x^2}=-\dfrac{x^2-1}{x^2}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-8cdda06475ffe134d106c48ad22c0dd4_l3.png)
Ker je , sledi, da sta točki
, sledi, da sta točki 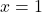 in
in 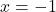 stacionarni točki funkcije
stacionarni točki funkcije  .
. - Zdaj določimo predznak prvega odvoda, torej območje naraščanja oziroma padanja.
Ker je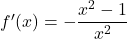 in je vedno
in je vedno 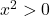 , moramo določiti predznak števca
, moramo določiti predznak števca 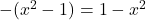 . Gre za kvadratno funkcijo, katere graf je konkavna parabola na sliki 21.1.
. Gre za kvadratno funkcijo, katere graf je konkavna parabola na sliki 21.1.
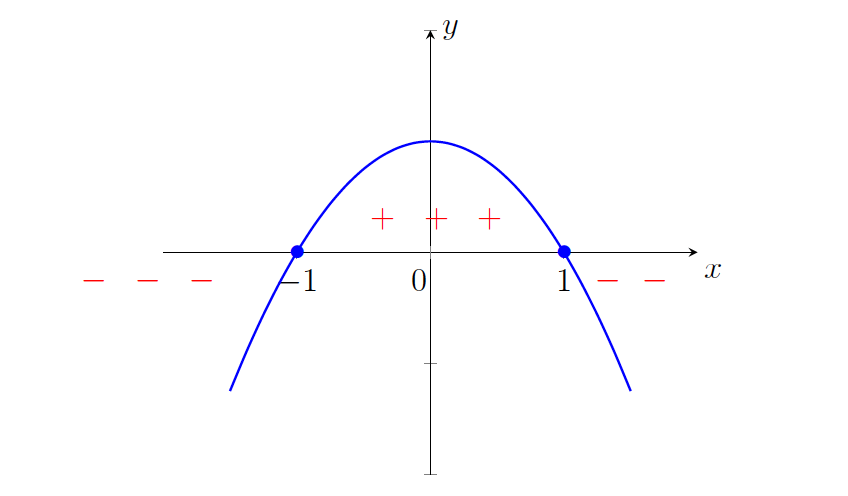
Slika 21.1: Graf kvadratne funkcije 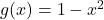 .
. - V naslednji tabeli bomo povzeli vse podatke, ki smo jih pridobili v prejšnjih točkah, in ugotovili intervale naraščanja oziroma padanja funkcije
 .
.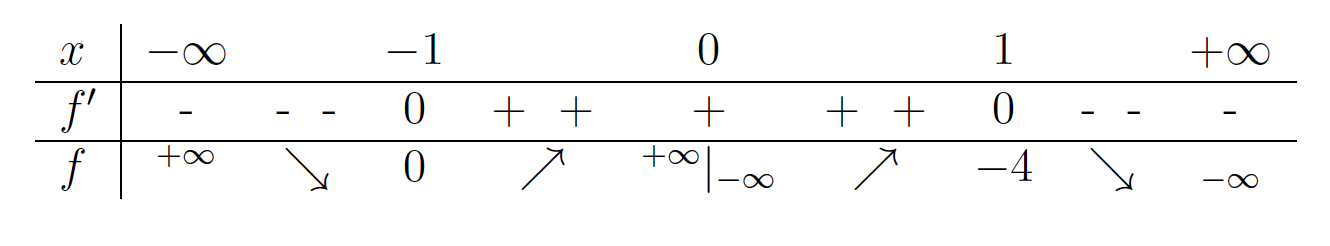 Funkcija narašča na uniji intervalov
Funkcija narašča na uniji intervalov 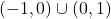 in pada na uniji intervalov
in pada na uniji intervalov 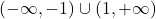 .
. - Graf funkcije
 je na sliki 21.2.
je na sliki 21.2.
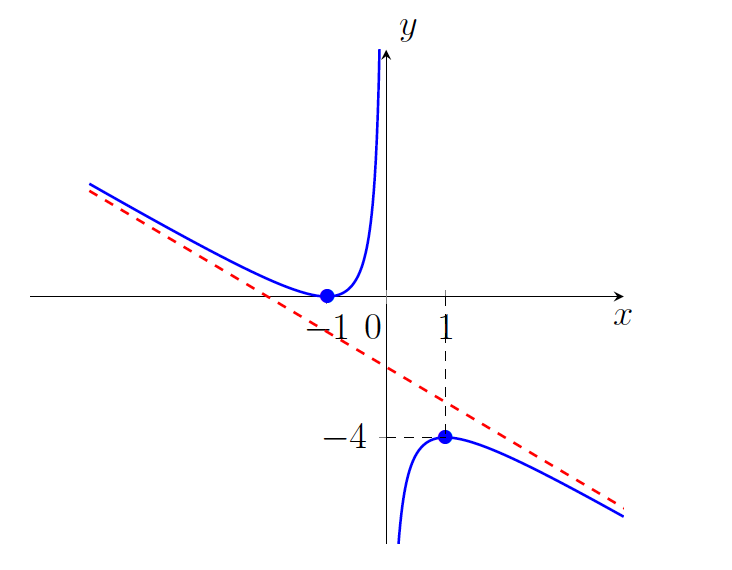
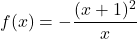 .
.Z grafa funkcije razberemo, da je funkcija ![]() konveksna na intervalu
konveksna na intervalu ![]() ter konkavna na intervalu
ter konkavna na intervalu ![]() .
.
Naloga 10: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]()
Rešitev:
- Dana funkcija je racionalna, torej je definirana tam, kjer je imenovalec različen od
 . Torej je domena funkcije
. Torej je domena funkcije 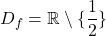 . Točka
. Točka 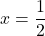 je pol funkcije in premica
je pol funkcije in premica 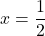 je navpična asimptota.
je navpična asimptota. - Ničle racionalne funkcije so ničle števca, torej dobimo
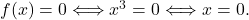 Funkcija ima samo eno ničlo, in sicer v točki
Funkcija ima samo eno ničlo, in sicer v točki  .
. - Poiščimo vse eventualne asimptote.
I) Najprej izračunamo limite dane funkcije, ko gre proti
proti 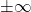 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \dfrac{x^3}{2x-1} = +\infty,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-8f499988b0b5d4f3f17687e6d42e9d08_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} \dfrac{x^3}{2x-1} = +\infty.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-554b75af6928a1e9a561c173e4feaff3_l3.png)
Funkcija torej nima vodoravnih asimptot, lahko pa ima poševne asimptote.
II) Ker je
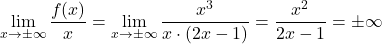 ,
,
ugotovimo, da funkcija nima niti poševnih asimptot.
III) V polu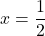 ima funkcija navpično asimptoto. Izračunamo enostranski limiti v tej točki:
ima funkcija navpično asimptoto. Izračunamo enostranski limiti v tej točki:
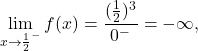
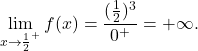
- Zdaj poiščimo stacionarne točke in lokalne ekstreme. Najprej izračunamo prvi odvod funkcije:
![Rendered by QuickLaTeX.com \[f'(x) = \dfrac{3x^2 \cdot (2x-1) - x^3 \cdot 2}{(2x-1)^2}= \frac{4x^3 - 3x^2}{(2x-1)^2}= \frac{x^2 \cdot (4x - 3)}{(2x-1)^2}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-f9f827ce3956e00e34440d1c007d702e_l3.png)
Ker je
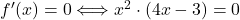 , sta točki
, sta točki 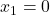 in
in 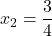 stacionarni točki.
stacionarni točki. - V naslednji tabeli bomo povzeli vse podatke, ki smo jih pridobili v prejšnjih točkah, in ugotovili intervale naraščanja oziroma padanja funkcije
 .
.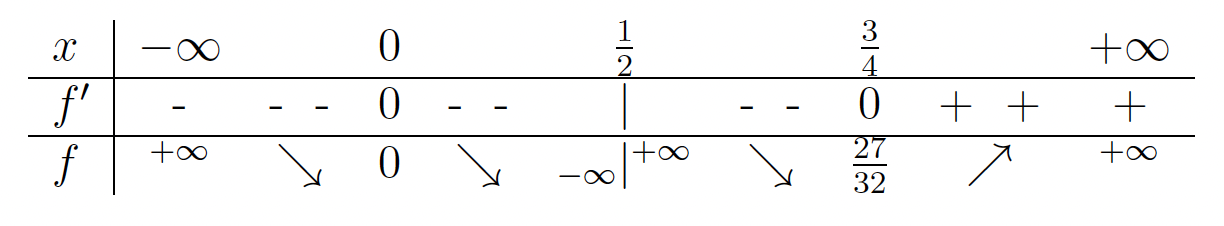 Funkcija pada na uniji intervalov
Funkcija pada na uniji intervalov 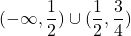 ter narašča na intervalu
ter narašča na intervalu 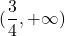 .
. - Zdaj imamo vse elemente za risanje grafa funkcije
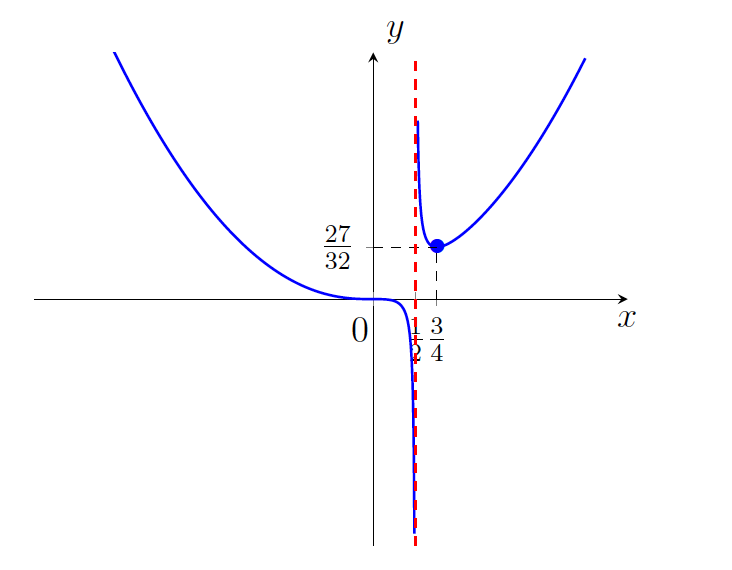
 ter razbiranje njene konveksnosti oziroma konkavnosti (glej sliko 21.3).
ter razbiranje njene konveksnosti oziroma konkavnosti (glej sliko 21.3).
 .
.Funkcija je konveksna na uniji intervalov ![]() ter konkavna na intervalu
ter konkavna na intervalu ![]() . Točka
. Točka ![]() je prevoj dane funkcije.
je prevoj dane funkcije.
Naloga 11: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]()
Rešitev:
- Dana funkcija je racionalna, torej je definirana tam, kjer je imenovalec različen od
 . Torej je domena funkcije
. Torej je domena funkcije 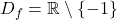 . Točka
. Točka 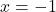 je pol funkcije in premica
je pol funkcije in premica 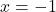 je navpična asimptota.
je navpična asimptota. - Ničle racionalne funkcije so ničle števca, torej dobimo
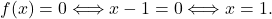 Edina ničla funkcije je v točki
Edina ničla funkcije je v točki  .
. - Poiščimo vse druge eventualne asimptote.
I) Izračunamo limite dane funkcije, ko gre proti
proti 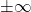 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to \pm\infty} f(x) = \lim_{x \to \pm\infty} \dfrac{x-1}{x^2+2x+1} =0,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-a2a3baef615ee716817b07c9819d665c_l3.png)
torej je premica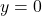 vodoravna asimptota funkcije
vodoravna asimptota funkcije  .
.
II) Ker ima funkcija vodoravno asimptoto, nima poševnih asimptot.
III) V polu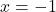 ima funkcija navpično asimptoto. Izračunamo enostranski limiti v polu:
ima funkcija navpično asimptoto. Izračunamo enostranski limiti v polu:
![Rendered by QuickLaTeX.com \[\lim_{x \to -1^-} f(x) = \frac{-2}{0^+} = - \infty=\lim_{x \to -1^+} f(x).\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-ef5e7f76fee1c16fd542db5fe81f638c_l3.png)
- Poiščimo stacionarne točke. Izračunamo prvi odvod funkcije:
![Rendered by QuickLaTeX.com \[f'(x) = \dfrac{1\cdot (x+1)^2 - (x-1) \cdot 2\cdot(x+1)}{(x+1)^4}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-9ef7d7639b666802b888753f16d76055_l3.png)
![Rendered by QuickLaTeX.com \[= \dfrac{(x+1)\cdot (x+1 -2x+2}{(x+1)^4}=\dfrac{3-x}{(x+1)^3}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-ba6b226368ad5556c53f1a7b6b9c5f35_l3.png)
Dobimo , torej je točka
, torej je točka 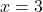 edina stacionarna točka.
edina stacionarna točka. - V naslednji tabeli bomo povzeli vse podatke, ki smo jih pridobili v prejšnjih točkah, in ugotovili intervale naraščanja oziroma padanja funkcije
 . Najprej opazimo, da je predznak imenovalca
. Najprej opazimo, da je predznak imenovalca 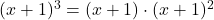 enak predznaku polinoma
enak predznaku polinoma 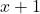 , saj je vedno
, saj je vedno 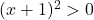 .
.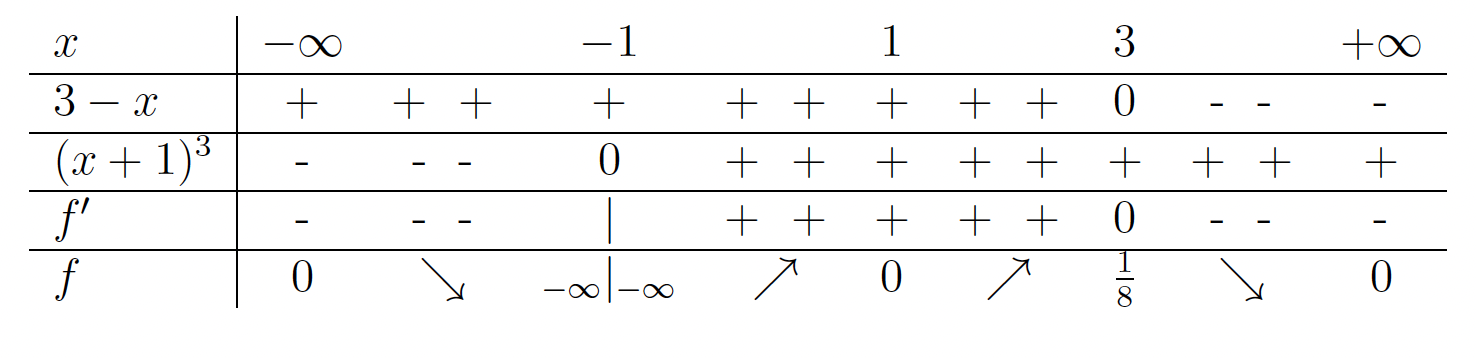 Funkcija pada na uniji intervalov
Funkcija pada na uniji intervalov 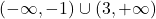 ter narašča na intervalu
ter narašča na intervalu 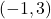 . Jasno je, da je v točki
. Jasno je, da je v točki  lokalni maksimum.
lokalni maksimum. - Zdaj imamo vse elemente za risanje grafa funkcije
 ter razbiranje njene konveksnosti oziroma konkavnosti (glej sliko 21.4).
ter razbiranje njene konveksnosti oziroma konkavnosti (glej sliko 21.4).
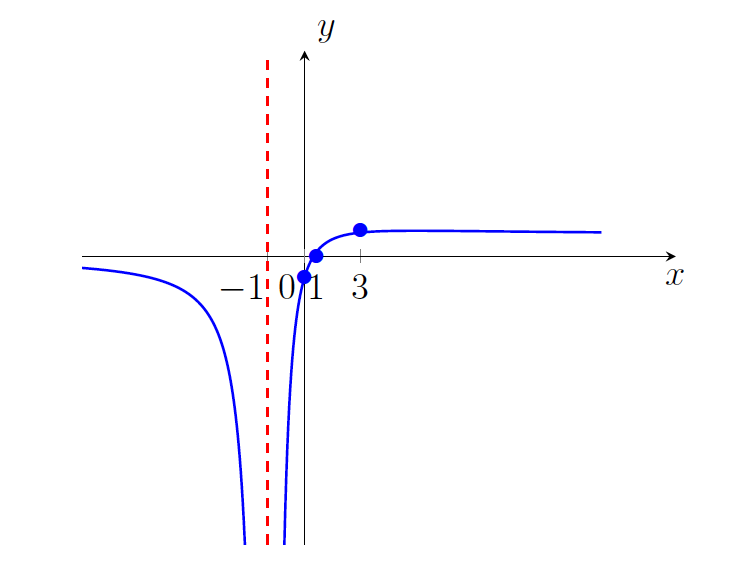
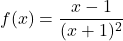 .
.Funkcija je konveksna na intervalu ![]() , kjer je
, kjer je ![]() prevoj funkcije, ter konkavna na uniji intervalov
prevoj funkcije, ter konkavna na uniji intervalov ![]() .
.
Naloga 12: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]()
Rešitev:
- Domena dane racionalne funkcje je
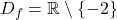 . Točka
. Točka 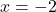 je pol funkcije in premica
je pol funkcije in premica 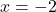 je navpična asimptota.
je navpična asimptota. - Ničle racionalne funkcije so ničle števca, torej dobimo
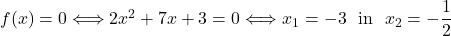 .
. - Poiščimo vse druge eventualne asimptote.
I) Izračunamo limite dane funkcije, ko gre proti
proti 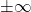 , in dobimo
, in dobimo 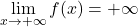 ter
ter 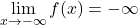 , torej funkcija
, torej funkcija  nima vodoravnih asimptot.
nima vodoravnih asimptot.
II) Poiščemo eventualne poševne asimptote. Najprej izračunamo limito
![Rendered by QuickLaTeX.com \[\lim_{x\to \pm\infty} \dfrac{f(x)}{x}=\lim_{x\to \pm\infty} \dfrac{2x^2+7x+3}{x^2+2x}=2=m\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-cd461f96fa0c35d0a1e5537cc8a9b5f1_l3.png)
in potem limito
![Rendered by QuickLaTeX.com \[\lim_{x\to \pm\infty} (f(x)-mx)&{=}\lim_{x\to \pm\infty} \left(\dfrac{2x^2+7x+3}{x+2}-2x\right){=}\lim_{x\to \pm\infty} \dfrac{2x^2+7x+3-2x^2-4x}{x+2}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-be704864e2421b4efd1cdecfa3839240_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x\to \pm\infty} \dfrac{3x+3}{x+2}=3=q.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-a95d92c5753345d78c4ba71cb901f454_l3.png)
Dobimo, da je premica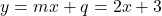 poševna asimptota funkcije
poševna asimptota funkcije  .
.
III) V polu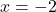 ima funkcija navpično asimptoto. Zdaj izračunamo enostranski limiti v polu:
ima funkcija navpično asimptoto. Zdaj izračunamo enostranski limiti v polu:
![Rendered by QuickLaTeX.com \[\lim_{x \to -2^-} f(x) = \lim_{x \to -2^-}\dfrac{(2x+1)\cdot (x+3)}{x+2}=\dfrac{-3\cdot 1}{0^-} = + \infty,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-a976bae3f201665ece59add365327454_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x \to -2^+} f(x) = \lim_{x \to -2^+}\dfrac{(2x+1)\cdot (x+3)}{x+2}=\dfrac{-3\cdot 1}{0^+} = - \infty.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-04216d50a9e644e7105ff897115def5a_l3.png)
- Poiščimo stacionarne točke. Izračunamo prvi odvod funkcije
 in dobimo:
in dobimo:
![Rendered by QuickLaTeX.com \[f'(x) = \dfrac{(4x+7)\cdot (x+2) - (2x^2+7x+3) \cdot 1}{(x+2)^2}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-81e9fdc30921037b8a32137f7115bf7d_l3.png)
![Rendered by QuickLaTeX.com \[= \dfrac{4x^2+8x+7x+14-2x^2-7x-3}{(x+2)^2}=\dfrac{2x^2+8x+11}{(x+2)^2}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-e8bd25e3285d63e876a34d6b8a9fe192_l3.png)
![Rendered by QuickLaTeX.com \[=\dfrac{2\cdot (x+2)^2+3}{(x+2)^2}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-fd27a1ee8907bc35bab529a22dd31e2e_l3.png)
Ker je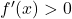 za vsak
za vsak  v domeni, sklepamo, da je funkcija
v domeni, sklepamo, da je funkcija  vedno naraščajoča in nima ekstremov.
vedno naraščajoča in nima ekstremov. - V naslednji tabeli bomo povzeli vse podatke, ki smo jih pridobili v prejšnjih točkah, in ugotovili intervale naraščanja oziroma padanja funkcije
 .
.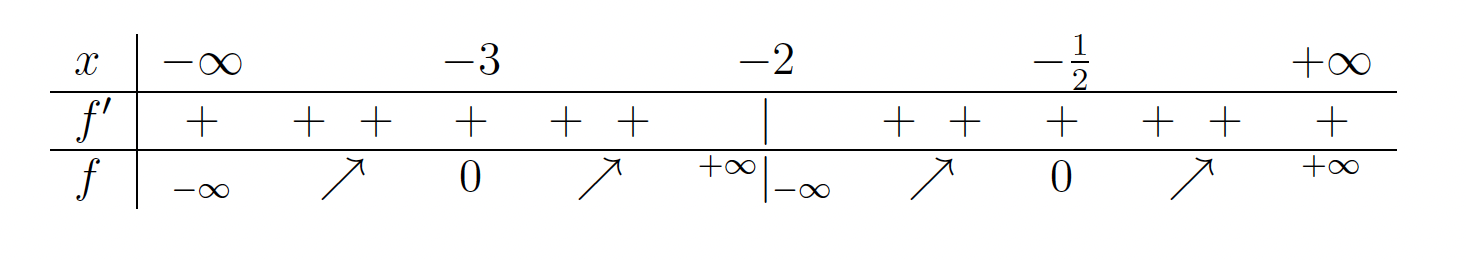
- Zdaj imamo vse elemente za risanje grafa funkcije
 ter razbiranje njene konveksnosti oziroma konkavnosti (glej sliko 21.5).
ter razbiranje njene konveksnosti oziroma konkavnosti (glej sliko 21.5).
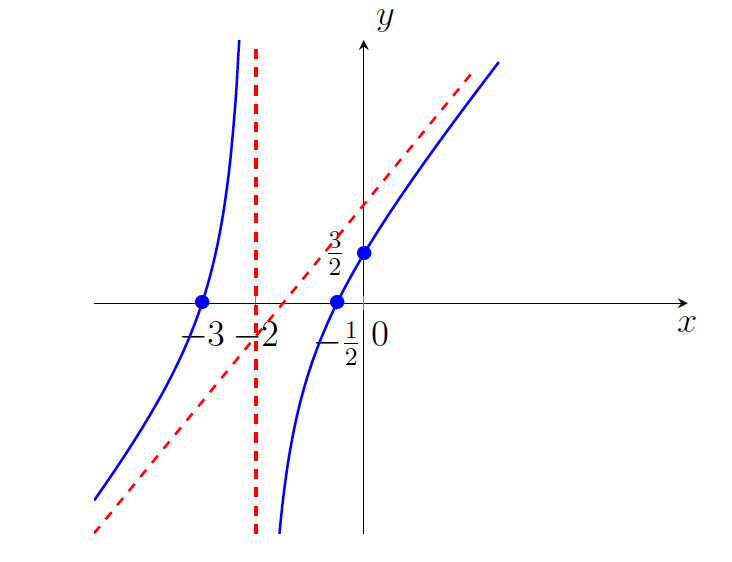
 .
.Funkcija je konveksna na intervalu ![]() ter konkavna na
ter konkavna na ![]() .
.
Naloga 13: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]() .
.
Rešitev:
- Domena dane racionalne funkcije je
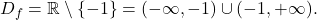 Točka
Točka 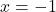 je pol funkcije in premica
je pol funkcije in premica 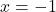 je navpična asimptota.
je navpična asimptota. - Ničle racionalne funkcije so ničle števca, torej dobimo
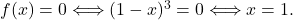
- Poiščimo vse eventualne druge asimptote.
I) Najprej izračunamo limite dane funkcije, ko gre proti
proti 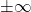 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \dfrac{1-3x+3x^2\boxed{-x^3}}{\boxed{x^2}+2x+1}= \lim_{x \to +\infty} (-x)=-\infty,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-32c971d26fcd592f7102cb5e595d717a_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} \dfrac{1-3x+3x^2\boxed{-x^3}}{\boxed{x^2}+2x+1}= \lim_{x \to -\infty} (-x)= +\infty.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-48f46574fbd4ee1a4d1ca795b008598f_l3.png)
Torej funkcija nima vodoravnih asimptot.
nima vodoravnih asimptot.
II) Zdaj poiščemo eventualne poševne asimptote. Najprej izračunamo limito
![Rendered by QuickLaTeX.com \[\lim_{x\to \pm\infty} \dfrac{f(x)}{x}=\lim_{x\to \pm\infty} \dfrac{\boxed{-x^3}+3x^2-3x+1}{\boxed{x^3}+2x^2+x}=-1=m\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4f3450e45adb1d266d252f8e47739520_l3.png)
in potem limito
![Rendered by QuickLaTeX.com \displaystyle\lim_{x\to \pm\infty} [f(x)-mx]&{=}\lim_{x\to \pm\infty} \left(\dfrac{-x^3+3x^2-3x+1}{x^2+2x+1}+x\right)](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-a8639c2bda839aa06702d08c4b6fe7b8_l3.png)
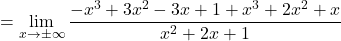
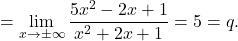
Dobimo, da je premica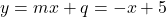 poševna asimptota funkcije
poševna asimptota funkcije  .
.
III) V polu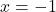 ima funkcija navpično asimptoto. Izračunamo enostranski limiti v polu:
ima funkcija navpično asimptoto. Izračunamo enostranski limiti v polu:
![Rendered by QuickLaTeX.com \[\lim_{x \to -1^-} f(x) = \lim_{x \to -1^-}\dfrac{(1-x)^3}{(1+x)^2}=\dfrac{2^3}{0^+} = + \infty=\lim_{x \to -1^+} f(x).\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5e5ba87b093be3c3d10fc4f87232febb_l3.png)
- Poiščimo stacionarne točke. Prvi odvod funkcije
 je:
je:
![Rendered by QuickLaTeX.com \[f'(x) &= \dfrac{3\cdot (1-x)^2\cdot (1-x)' \cdot (1+x)^2 -(1-x)^3\cdot 2\cdot(1+x)\cdot (1+x)'}{(1+x)^4}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-c11b34c3a85fee3caf5c895d98cb5a6c_l3.png)
![Rendered by QuickLaTeX.com \[= \dfrac{-(1-x)^2\cdot (1+x)\cdot (3+3x+2-2x}{(1+x)^4}=\dfrac{-(1-x)^2\cdot (x+5)}{(1+x)^3}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-8e9568f371bdb144e47f640d583ab758_l3.png)
Dobimo za
za 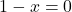 ali
ali 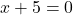 , torej sta točki
, torej sta točki 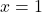 in
in 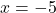 stacionarni točki.
stacionarni točki. - V naslednji tabeli bomo povzeli vse podatke, ki smo jih pridobili v prejšnjih točkah, in ugotovili intervale naraščanja oziroma padanja funkcije
 . Najprej opazimo, da je predznak imenovalca
. Najprej opazimo, da je predznak imenovalca 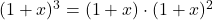 enak predznaku polinoma
enak predznaku polinoma 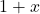 , saj je vedno
, saj je vedno 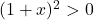 . Podobno je vedno pozitiven tudi polinom
. Podobno je vedno pozitiven tudi polinom 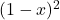 . Torej je predznak odvoda podan s predznakoma polinomov
. Torej je predznak odvoda podan s predznakoma polinomov 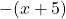 in
in 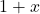 .
.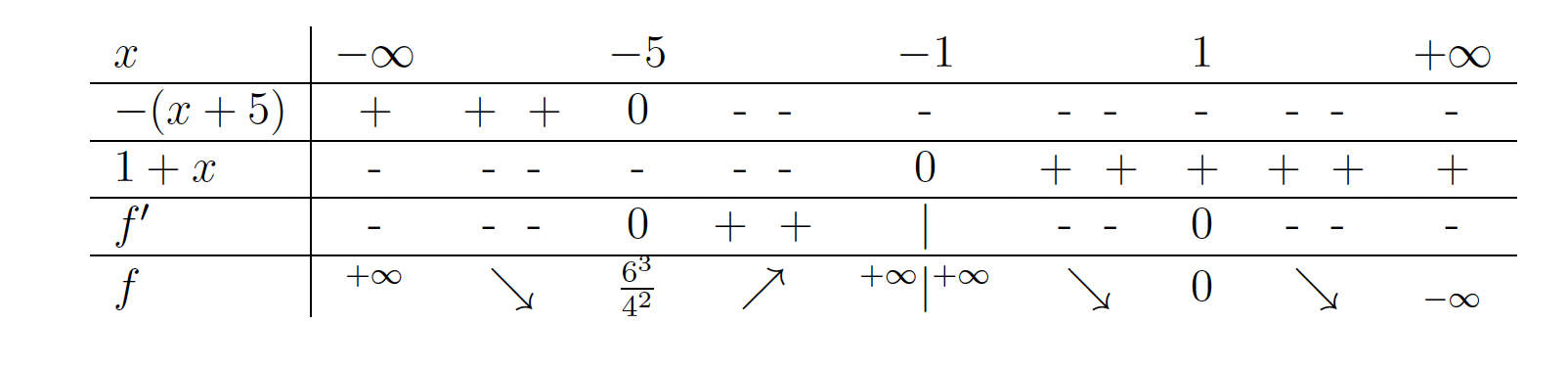 Funkcija pada na uniji intervalov
Funkcija pada na uniji intervalov 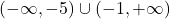 ter narašča na intervalu
ter narašča na intervalu 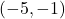 . Jasno je, da je v točki
. Jasno je, da je v točki 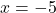 lokalni minimum.
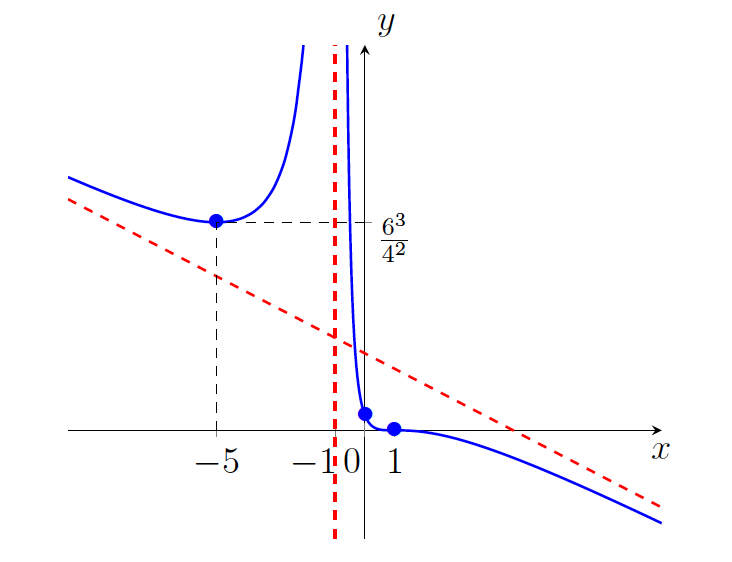
lokalni minimum. - Zdaj imamo vse elemente za risanje grafa funkcije
 ter razbiranje njene konveksnosti oziroma konkavnosti (glej sliko 21.6).
ter razbiranje njene konveksnosti oziroma konkavnosti (glej sliko 21.6).
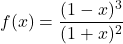 .
.Funkcija je konveksna na uniji intervalov ![]() ter konkavna na intervalu
ter konkavna na intervalu ![]() . Točka
. Točka ![]() je prevoj funkcije
je prevoj funkcije ![]() .
.
Naloga 14: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]()
Rešitev:
- Dana funkcija je racionalna, torej je definirana, kjer je imenovalec različen od
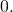 Ker je
Ker je 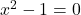 za
za 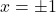 , je domena funkcije
, je domena funkcije 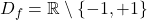 . Točki
. Točki 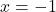 in
in  sta pola ter premici
sta pola ter premici 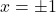 sta navpični asimptoti dane funkcije.
sta navpični asimptoti dane funkcije. - Ničle racionalne funkcije so ničle števca, torej je
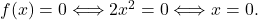
- Poiščimo vse eventualne druge asimptote.
I) Izračunamo limite dane funkcije, ko gre proti
proti 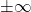 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to \pm\infty} f(x) = \lim_{x \to \pm\infty} \frac{2x^2}{x^2-1} = 2.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-8253240e90df4cc5efc87855de929381_l3.png)
Dobimo, da je premica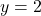 vodoravna asimptota.
vodoravna asimptota.
II) Ker ima funkcija vodoravno asimptoto na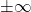 , vemo, da zagotovo nima poševnih asimptot.
, vemo, da zagotovo nima poševnih asimptot.
III) Premici in
in 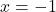 sta navpični asimptoti in enostranski limiti v točkah
sta navpični asimptoti in enostranski limiti v točkah 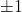 so:
so:
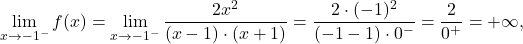
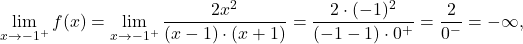
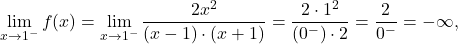
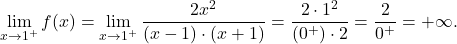
- Poiščimo stacionarne točke in lokalne ekstreme funkcije
 . Prvi odvod dane funkcije ima obliko
. Prvi odvod dane funkcije ima obliko
![Rendered by QuickLaTeX.com \[f'(x) = \dfrac{4x \cdot (x^2-1) - 2x^2 \cdot (2x)}{(x^2-1)^2}= \dfrac{-4x}{(x^2-1)^2},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5ff3376b7f1a0629690f7b1c176ce156_l3.png)
zato je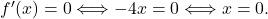 Točka
Točka 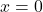 je edina stacionarna točka funkcije
je edina stacionarna točka funkcije  .
.
Zdaj izračunamo drugi odvod funkcije :
:
![Rendered by QuickLaTeX.com \[f''(x)&=\dfrac{-4(x^2-1)^2-(-4x)\cdot 2\cdot (x^2-1)\cdot 2x}{(x^2-1)^4}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-50fc387a2cbdeeb91b3bcdc028bea930_l3.png)
![Rendered by QuickLaTeX.com \[=\dfrac{(x^2-1)\cdot (-4x^2+4+16x^2}{(x^2-1)^4}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-2955a489bb309fa84eaf191ac285e46b_l3.png)
![Rendered by QuickLaTeX.com \[=\dfrac{4\cdot (3x^2+1)}{(x^2-1)^3}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-f744d3fd69eef8e023ea46e0395089ee_l3.png)
Vrednost drugega odvoda v stacionarni točki je
je 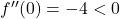 , kar pomeni, da je v točki
, kar pomeni, da je v točki  lokalni maksimum funkcije
lokalni maksimum funkcije  .
.
Ker lahko zapišemo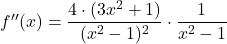 in je
in je 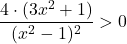 za vsak
za vsak  , sledi, da je predznak drugega odvoda enak predznaku kvadratne funkcije
, sledi, da je predznak drugega odvoda enak predznaku kvadratne funkcije 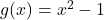 . Torej je
. Torej je  natanko tedaj, ko je
natanko tedaj, ko je 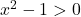 oziroma
oziroma 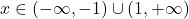 , in je
, in je  natanko tedaj, ko je
natanko tedaj, ko je 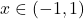 .
. - V naslednji tabeli bomo povzeli vse podatke, ki smo jih pridobili v prejšnjih točkah, in ugotovili intervale naraščanja oziroma padanja ter konveksnosti oziroma konkavnosti funkcije
 .
.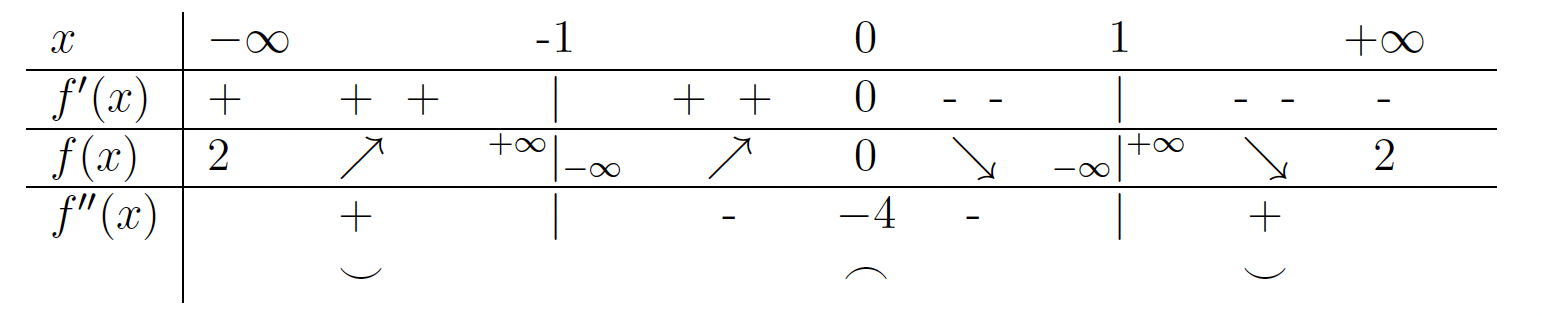 Funkcija
Funkcija  je naraščajoča na uniji intervalov
je naraščajoča na uniji intervalov 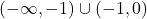 ter padajoča na uniji intervalov
ter padajoča na uniji intervalov 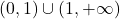 . Poleg tega je funkcija konkavna na intervalu
. Poleg tega je funkcija konkavna na intervalu 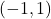 ter konveksna na uniji intervalov
ter konveksna na uniji intervalov 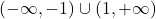 .
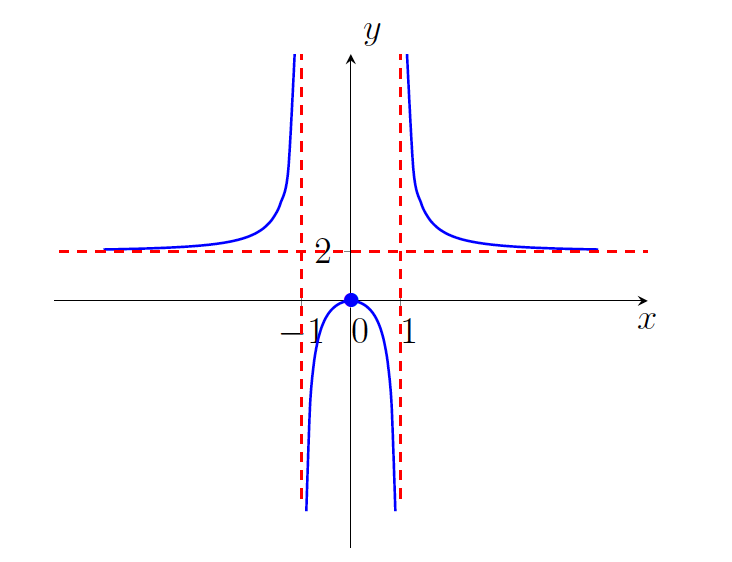
. - Na podlagi prejšnje tabele bomo narisali graf funkcije
 (glej sliko 21.7).
(glej sliko 21.7).
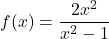 .
.Naloga 15: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]() .
.
Rešitev:
- Dana funkcija je povsod definirana, torej je njena domena
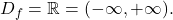
- Ničle funkcije so rešitve enačbe
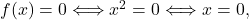 ker je vedno
ker je vedno 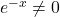 .
.
Funkcija nima polov. - Poiščimo vse eventualne asimptote.
I) Ker funkcija nima polov, nima niti navpičnih asimptot.
II) Zdaj izračunamo limite dane funkcije, ko gre proti
proti 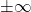 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} x^2\cdot e^{-x}= (+\infty)\cdot e^{-(-\infty)}=+\infty,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-a58387bd37a26f5abf11a62828c263e9_l3.png)
torej funkcija nima vodoravne asimptote, ko gre proti
proti  .
.
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} x^2\cdot e^{-x}= \lim_{x \to +\infty} \dfrac{x^2}{e^x}\stackrel{\left[\frac{+\infty}{+\infty}\right]}{\underset{\text{L'H}}{=}}\lim_{x \to +\infty} \dfrac{2x}{e^x}\stackrel{\left[\frac{+\infty}{+\infty}\right]}{\underset{\text{L'H}}{=}}\lim_{x \to +\infty} \dfrac{2}{e^x}=0^{+}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-0e5e6a6b40dc0f084a007552e8042b27_l3.png) Torej, premica
Torej, premica 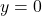 je vodoravna asimptota, ko gre
je vodoravna asimptota, ko gre  proti
proti 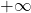 .
.
III) Funkcija nima poševnih asimptot, ker ima vodoravno asimptoto pri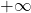 ; pri
; pri  pa dobimo
pa dobimo
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} \dfrac{f(x)}{x}=\lim_{x \to -\infty} x\cdot e^{-x}=(-\infty)\cdot (+\infty)=-\infty.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-f9762df7d1ea6912ba2dc68343a29ca3_l3.png)
- Poiščimo stacionarne točke. To so ničle prvega odvoda, ki ima obliko:
![Rendered by QuickLaTeX.com \[f'(x) = 2x\cdot e^{-x}+x^2\cdot e^{-x}\cdot (-1)=e^{-x}\cdot (2x-x^2).\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-122c05536465163e85239087a96bea8d_l3.png) Ker je
Ker je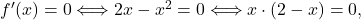 sta
sta 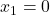 in
in 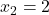 stacionarni točki. Zdaj izračunamo vrednost drugega odvoda funkcije
stacionarni točki. Zdaj izračunamo vrednost drugega odvoda funkcije  v stacionarnih točkah.
v stacionarnih točkah.
Ker je
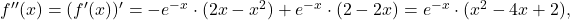 dobimo
dobimo 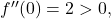 kar pomeni, da je v točki
kar pomeni, da je v točki  lokalni minimum. Ker je
lokalni minimum. Ker je 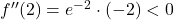 , sklepamo še, da je v točki
, sklepamo še, da je v točki  lokalni maksimum.
lokalni maksimum.
Poiščemo tudi prevoje in dobimo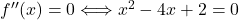 , torej sta točki
, torej sta točki 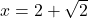 in
in 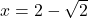 prevoja funkcije
prevoja funkcije  .
. - Zdaj preštudiramo predznak prvega odvoda
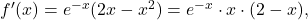 pomagamo si z naslednjo tabelo. Vemo, da je eksponentna funkcija
pomagamo si z naslednjo tabelo. Vemo, da je eksponentna funkcija 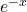 vedno pozitivna, torej je predznak prvega odvoda podan s predznakom produkta
vedno pozitivna, torej je predznak prvega odvoda podan s predznakom produkta 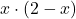 .
.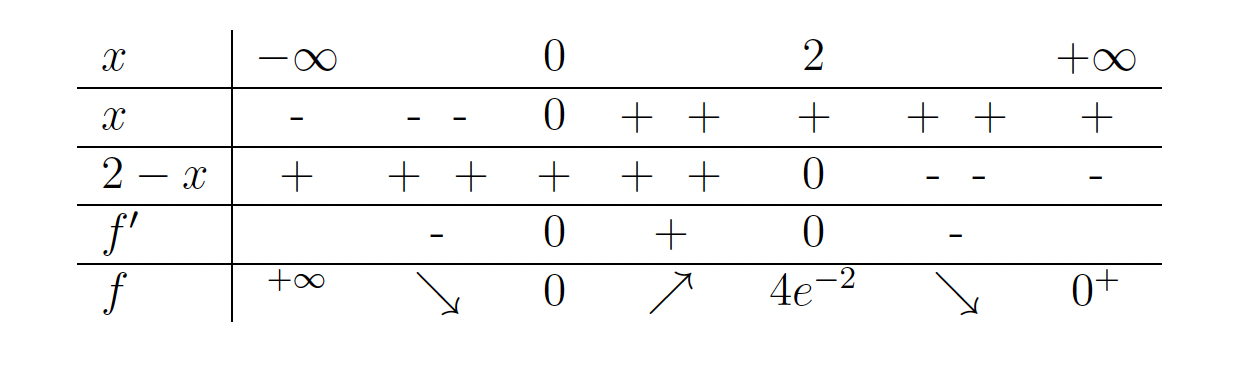 Dana funkcija
Dana funkcija  je naraščajoča na intervalu
je naraščajoča na intervalu  , padajoča pa na uniji intervalov
, padajoča pa na uniji intervalov  .
. - Na podlagi prejšnje tabele narišemo graf funkcije
 (glej sliko 21.8).
(glej sliko 21.8).
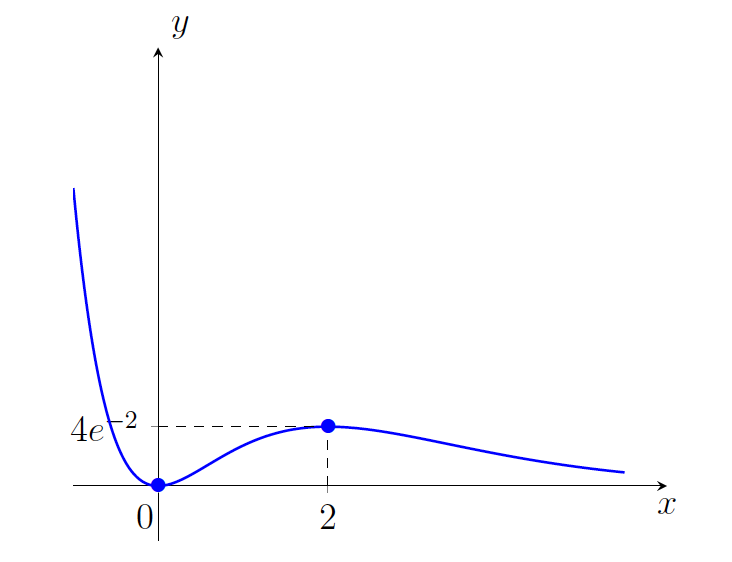
 .
.Z grafa funkcije razberemo intervale konveksnosti oziroma konkavnosti, saj vemo, kateri točki sta prevoja. Funkcija je konveksna na uniji intervalov ![]() ter konkavna na intervalu
ter konkavna na intervalu ![]() .
.
Naloga 16: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]() .
.
Rešitev:
- Ker je dana funkcija povsod definirana (je namreč produkt med linearno funkcijo
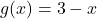 in eksponentno funkcijo
in eksponentno funkcijo 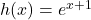 , obe funkciji pa sta definirani na
, obe funkciji pa sta definirani na  ), je njena domena
), je njena domena 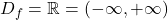 .
. - Ničle funkcije so rešitve enačbe
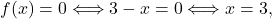 ker eksponentna funkcija ni nikoli enaka
ker eksponentna funkcija ni nikoli enaka  .
.
Funkcija nima polov. - Poiščimo vse eventualne asimptote.
I) Ker funkcija nima polov, nima niti navpičnih asimptot.
II) Zdaj izračunamo limite dane funkcije pri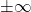 :
:
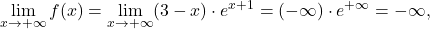
torej funkcija nima vodoravne asimptote, ko gre proti
proti 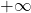 . Poleg tega dobimo:
. Poleg tega dobimo:
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} (3-x)\cdot e^{x+1}\stackrel{ \left[+\infty\cdot 0\right]}{=}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5646e92af93cb8f9eb4becdce92e6b16_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} \dfrac{3-x}{e^{-(x+1)}}\stackrel{\left[\frac{+\infty}{+\infty}\right]}{\underset{\text{L'H}}{=}}\lim_{x \to -\infty} \dfrac{-1}{e^{-(x+1)}\cdot (-1)}=0^{+},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4d7a0815eaaa64bf1c8bcf50a1785fc7_l3.png) kjer je
kjer je 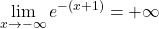 .
.
Torej, premica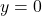 je vodoravna asimptota, ko gre
je vodoravna asimptota, ko gre  proti
proti  .
.
III) Raziskati moramo obstoj poševnih asimptot v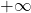 , saj vodoravna asimptota ne obstaja:
, saj vodoravna asimptota ne obstaja:
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} \dfrac{f(x)}{x}=\lim_{x \to +\infty} \dfrac{(3-x)\cdot e^{x+1}}{x}= \lim_{x \to +\infty} \dfrac{(3-x)}{x}\cdot e^{x+1}=(-1)\cdot (e^{+\infty})=-\infty,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-45737cbaee8d5131076291177ea7af69_l3.png)
kar pomeni, da funkcija nima poševnih asimptot. - Poiščimo stacionarne točke oziroma ničle prvega odvoda:
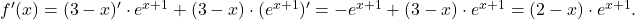
Ker je , je
, je  stacionarna točka. Zdaj izračunamo vrednost drugega odvoda funkcije
stacionarna točka. Zdaj izračunamo vrednost drugega odvoda funkcije  v stacionarni točki. Odvajamo prvi odvod in dobimo
v stacionarni točki. Odvajamo prvi odvod in dobimo 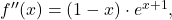 torej je
torej je 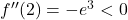 , kar pomeni, da ima dana funkcija v točki
, kar pomeni, da ima dana funkcija v točki  lokalni maksimum. Poiščemo tudi prevoje in dobimo
lokalni maksimum. Poiščemo tudi prevoje in dobimo 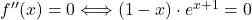 , torej je točka
, torej je točka  prevoj.
prevoj. - Na podlagi tabele 21.1 identificiramo intervale naraščanja oziroma padanja ter intervale konveksnosti oziroma konkavnosti. Predznak prvega odvoda
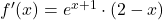 je enak predznaku linearne funkcije
je enak predznaku linearne funkcije 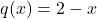 , torej je pozitiven za
, torej je pozitiven za 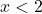 in negativen za
in negativen za 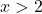 . Podobno določimo predznak drugega odvoda
. Podobno določimo predznak drugega odvoda 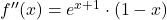 na podlagi predznaka linearne funkcije
na podlagi predznaka linearne funkcije 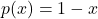 in dobimo:
in dobimo:  za
za 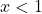 ter
ter  za
za 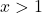 . Ugotovimo, da je funkcija
. Ugotovimo, da je funkcija  naraščajoča na intervalu
naraščajoča na intervalu 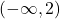 , padajoča pa na intervalu
, padajoča pa na intervalu  Funkcija je konveksna na intervalu
Funkcija je konveksna na intervalu  , konkavna pa na intervalu
, konkavna pa na intervalu  .
.
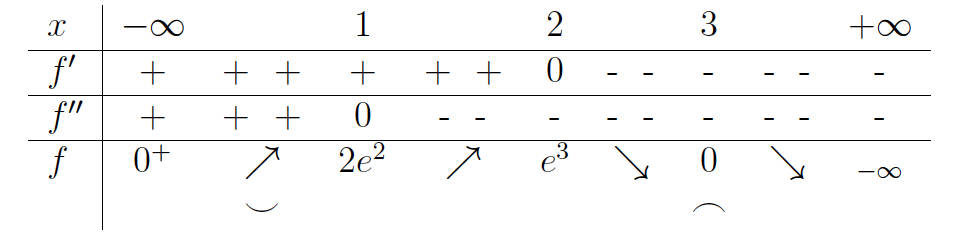
Tabela 21.1: Intervali naraščanja in padanja ter konveksnosti in konkavnosti funkcije 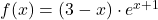 .
. - Na podlagi prejšnje tabele bomo narisali graf funkcije
 (glej sliko 21.9).
(glej sliko 21.9).
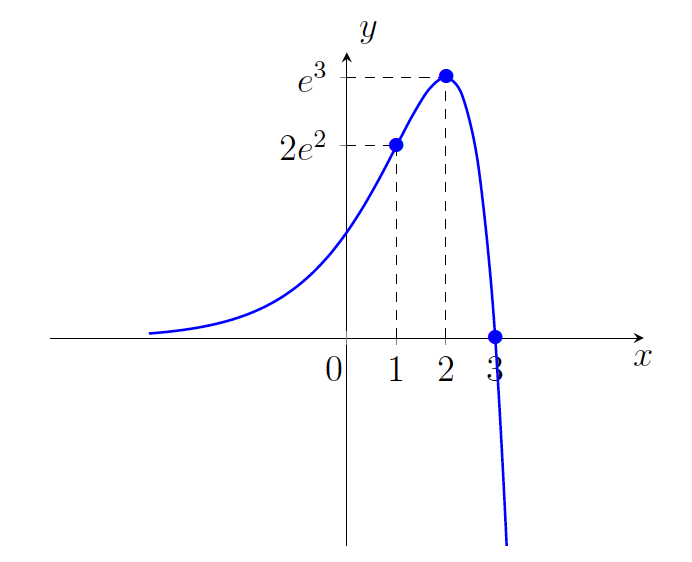
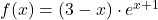 .
.Naloga 17: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]() .
.
Rešitev: Da bi preučili to funkcijo, jo bomo zapisali kot eksponentno funkcijo:
![]()
- Dana funkcija je definirana tam, kjer je definirana logaritemska funkcija
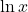 , zato je njena domena
, zato je njena domena 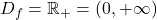 .
. - Ničle funkcije so rešitve enačbe
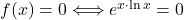 , vendar ne obstajajo.
, vendar ne obstajajo.
Funkcija tudi nima polov. - Poiščimo vse eventualne asimptote.
I) Ker funkcija nima polov, nima niti navpičnih asimptot. Ker je eksponentna funkcija zvezna, lahko izračunamo limito:
![Rendered by QuickLaTeX.com \[\lim_{x \to 0^+} f(x) &= \lim_{x \to 0^+} e^{x\cdot \ln x}\ \ \stackrel{e^{\left[0\cdot (-\infty)\right]}}{=} e^{\displaystyle\lim_{x \to 0^+} \dfrac{\ln x}{1/x}} \ \ \stackrel{e^{\left[\frac{-\infty}{+\infty}\right]}}{\underset{\text{L'H}}{=}}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-96470dba83c0a3d5072c6b1bebef0478_l3.png)
![Rendered by QuickLaTeX.com \[e^{\displaystyle\lim_{x \to 0^+} \dfrac{1/x}{-1/x^2}}=e^{\displaystyle\lim_{x \to 0^+} (-x)}=e^0=1.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5996f8a4e3aa23438cd9e96fb091b269_l3.png)
II) Zdaj izračunamo limito dane funkcije v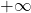 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} e^{x\cdot \ln x}= e^{+\infty}=+\infty,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-ab3ebf31a6080c7e26915020420dd847_l3.png)
torej funkcija nima vodoravne asimptote v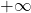 .
.
III) Preverimo, ali ima funkcija poševno asimptoto v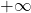 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} \dfrac{f(x)}{x}=\lim_{x \to +\infty} \dfrac{e^{x\cdot \ln x}}{x}\stackrel{\left[\frac{+\infty}{+\infty}\right]}{\underset{\text{L'H}}{=}} \lim_{x \to +\infty} \dfrac{e^{x\cdot \ln x}\cdot (\ln x+1)}{1}=+\infty,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-3504a4ef533290041cac7f9ee6828528_l3.png)
torej funkcija nima poševnih asimptot. - Poiščimo stacionarne točke. To so ničle prvega odvoda, ki ima obliko:
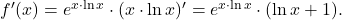
Ker je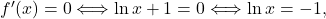 sledi, da je
sledi, da je 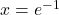 stacionarna točka. Izračunamo drugi odvod funkcije in dobimo:
stacionarna točka. Izračunamo drugi odvod funkcije in dobimo:
![Rendered by QuickLaTeX.com \[f''(x)=e^{x\cdot \ln x}\cdot (\ln x+1)^2+e^{x\cdot \ln x}\cdot \dfrac{1}{x}=e^{x\cdot \ln x}\cdot\left[(\ln x+1)^2+\dfrac{1}{x}\right].\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-7c4aae60f9c93bb48ee96c85ccc13651_l3.png)
Ugotovimo, da je vrednost drugega odvoda funkcije vedno pozitivna za vse
vedno pozitivna za vse  v domeni (tj.
v domeni (tj. 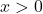 ), torej je funkcija
), torej je funkcija  povsod konveksna. Poleg tega je v točki
povsod konveksna. Poleg tega je v točki 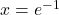 lokalni minimum.
lokalni minimum. - Zdaj določimo predznak prvega odvoda, torej območje naraščanja oziroma padanja.
![Rendered by QuickLaTeX.com \[f'(x)>0 \Longleftrightarrow e^{x\cdot \ln x}\cdot (\ln x+1)>0 \Longleftrightarrow \ln x+1>0 \Longleftrightarrow \ln x> -1\Longleftrightarrow x> e^{-1},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-9ba160de379273c03cfd686c7a0d2e8e_l3.png)
torej funkcija narašča na intervalu
narašča na intervalu 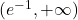 in pada na intervalu
in pada na intervalu 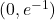 .
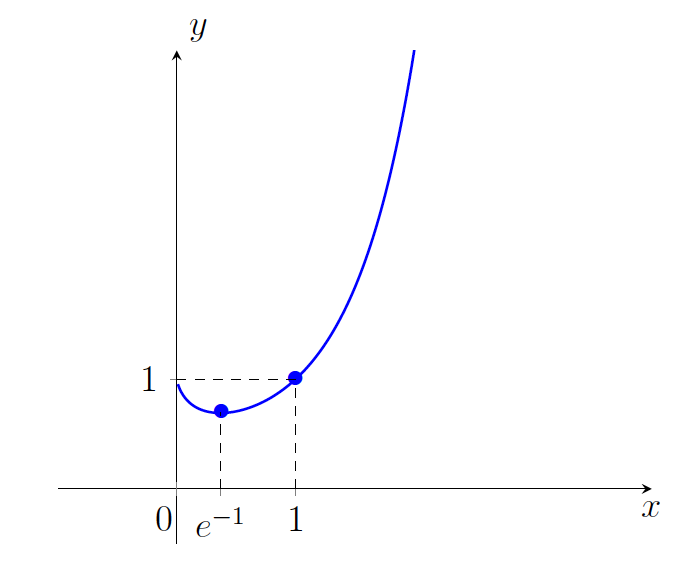
. - Zdaj imamo vse elemente za risanje grafa funkcije
 (glej sliko 21.10).
(glej sliko 21.10).
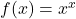 .
.Naloga 18: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]() .
.
Rešitev:
- Ker je definicijsko območje korenske funkcije s sodim korenskim eksponentom
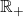 , je domena funkcije
, je domena funkcije  množica vseh vrednosti
množica vseh vrednosti  , za katere je
, za katere je 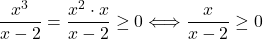 , ker je
, ker je 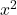 vedno pozitiven. Rešimo neenačbo ob pomoči naslednje tabele:
vedno pozitiven. Rešimo neenačbo ob pomoči naslednje tabele:
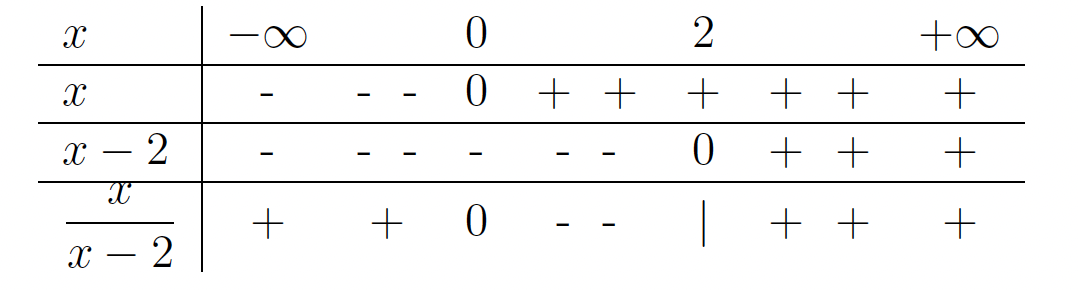
Torej je![Rendered by QuickLaTeX.com \dfrac{x^3}{x-2} \geq 0 \Longleftrightarrow x\in (-\infty,0] \cup (2,+\infty)](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-011cec361861bbad81401c9d10b490a3_l3.png) in zato je
in zato je ![Rendered by QuickLaTeX.com D_f=(-\infty,0] \cup (2,+\infty)](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-8257e73717ac26038b72963d6b13e85a_l3.png) .
. - Ničle funkcije so rešitve enačbe
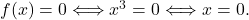
- Funkcija ima samo en pol, ki je ničla imenovalca, tj.
 in premica
in premica  je tako navpična asimptota dane funkcije. Desna limita v točki
je tako navpična asimptota dane funkcije. Desna limita v točki  je
je
![Rendered by QuickLaTeX.com \[\lim_{x \to 2^+} f(x) = \lim_{x \to 2^+}\sqrt{ \frac{x^3}{x-2}} = \sqrt{\frac{2^3}{0^+}} = +\infty.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-72c1970468356386099329b2257831f1_l3.png)
Izračunali smo samo desno limito v točki , ker funkcija na levi strani te točke ni definirana.
, ker funkcija na levi strani te točke ni definirana. - Poiščimo vse druge eventualne asimptote.
I) Zdaj izračunamo limite dane funkcije v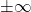 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to \pm\infty} f(x) {=} \lim_{x \to \pm\infty} \sqrt{ \dfrac{x^3}{x-2}}{ =} \lim_{x \to \pm\infty} \sqrt{\dfrac{x^2\cdot x}{x-2}}{ =} \lim_{x \to \pm\infty} \left(\lvert x\rvert\cdot \sqrt{\boxed{ \dfrac{x}{x-2}} }_{\searrow 1}\right)=+\infty.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-9b0326caf78547f852caa8ad9e5ca0dc_l3.png)
Torej, funkcija nima vodoravnih asimptot.
II) Preverimo, ali ima funkcija poševno asimptoto v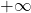 .
.
Najprej izračunamo limito
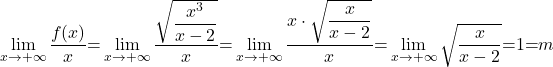
in nato drugo limito
![Rendered by QuickLaTeX.com \[q=\lim_{x \to +\infty} [f(x) - mx] = \lim_{x \to +\infty} \left(\sqrt \frac{x^3}{x-2} - x\right)\stackrel{[\infty-\infty]}{=}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-762e57c995a107ebbe55ac9f85b0ebc5_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x \to +\infty} \left(\sqrt \frac{x^3}{x-2} - x\right) \cdot \dfrac{\sqrt{\dfrac{x^3}{x-2}}+x}{\sqrt{\dfrac{x^3}{x-2}}+x}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-6e1e6b687c6e5ec9ea6dfdc07e3915c1_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x \to +\infty} \dfrac{\left(\sqrt{\dfrac{x^3}{x-2}}\right)^2-x^2}{\sqrt{\dfrac{x^2\cdot x}{x-2}}+x}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-633ee4cd8bd85a1737188af6e6717ad6_l3.png)
![Rendered by QuickLaTeX.com \[= \lim_{x \to +\infty} \dfrac{\dfrac{x^3}{x-2}-x^2}{x\sqrt{\dfrac{x}{x-2}}+x}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4aa9682630ea7500eb86b72e5cd486ef_l3.png)
![Rendered by QuickLaTeX.com \[= \lim_{x \to +\infty} \dfrac{x^3 - x^3 + 2x^2}{(x-2) \cdot x\cdot \left(\boxed{\sqrt{\frac{x}{x-2}}}_{\searrow 1}+1\right)}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-04ec5b997ec8dac1e166a8069ffb5ce6_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x \to +\infty} \dfrac{ 2x^2}{(x^2 - 2x) \cdot 2} =1.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-fc51bd29e1a66885268ffcd2ce641d26_l3.png)
Torej, premica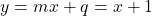 je poševna asimptota funkcije
je poševna asimptota funkcije  , ko gre
, ko gre  proti
proti 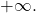
Zdaj izračunamo vrednosti in
in 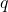 , ko
, ko  gre proti
gre proti  :
:
![Rendered by QuickLaTeX.com \[m=\lim_{x \to -\infty} \dfrac{f(x)}{x} = \lim_{x \to -\infty} \dfrac{\sqrt{ \dfrac{x^3}{x-2}}}{x}= \lim_{x \to -\infty} \dfrac{\sqrt{ \dfrac{x^2\cdot x}{x-2}}}{x}= \lim_{x \to -\infty} \dfrac{\lvert x\rvert\cdot\sqrt{ \dfrac{x}{x-2}}}{x}=\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-064a48dac393614ae5880b69bb453ff0_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x \to -\infty} \dfrac{-x \sqrt {\dfrac{x}{x-2}}}{x} = \lim_{x \to -\infty} -\sqrt{ \dfrac{x}{x-2}} = -1\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-835cc13e5f9fd1ad52f19f445f27e125_l3.png)
in potem
![Rendered by QuickLaTeX.com \[q = \lim_{x \to -\infty} [f(x) - mx] = \lim_{x \to -\infty} \left(\sqrt{ \dfrac{x^3}{x-2}} + x\right)\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4c611466f59fbccadc371b5354fe896a_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x \to -\infty} \left(-x \sqrt {\dfrac{x}{x-2} }+ x\right)\stackrel{[\infty-\infty]}{=}\\ &= \lim_{x \to -\infty} \left(-x \sqrt{ \dfrac{x}{x-2}} + x\right) \cdot \dfrac{x \sqrt{\dfrac{x}{x-2}}+x}{x\sqrt{\dfrac{x}{x-2}}+x}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-dc127cee1650f871a923b8549790e822_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x \to -\infty} \dfrac{x^2 - \dfrac{x^3}{x-2}}{x \left(\sqrt{\dfrac{x}{x-2}}+1\right)}= \lim_{x \to -\infty} \dfrac{x^3 - 2x^2 - x^3}{(x-2)\cdot x\cdot \left(\boxed{\sqrt{\dfrac{x}{x-2}}+1}_{\searrow 2}\right)} = -1.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-ecf0e5d8b9a8c44bfe6f894daf8b6c99_l3.png)
Torej, premica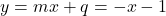 je poševna asimptota funkcije
je poševna asimptota funkcije  , ko gre
, ko gre  proti
proti  .
. - Stacionarne točke so ničle prvega odvoda, ki ima obliko:
![Rendered by QuickLaTeX.com \[f'(x) =\left(\sqrt{\frac{x^3}{x-2}}\right)' = \dfrac{1}{2\sqrt{\dfrac{x^3}{x-2}}} \cdot \left(\frac{x^3}{x-2}\right)'\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-e7f02941c0a2e09e571606d30c5ebd6a_l3.png)
![Rendered by QuickLaTeX.com \[= \dfrac{1}{2\sqrt{\dfrac{x^3}{x-2}}} \cdot \dfrac{3x^2 \cdot (x-2) - x^3}{(x-2)^2} = \dfrac{\sqrt{x-2}}{2\sqrt{x^3}} \cdot \dfrac{x^2\cdot (3x-6-x)}{(x-2)^2}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-24ee7ed11c0b52a5643b7f29cb14cb29_l3.png)
![Rendered by QuickLaTeX.com \[=\dfrac{x^2 \cdot \sqrt{x-2} \cdot (x-3)}{\sqrt{x^3} \cdot \sqrt{(x-2)^4}}\\ & = (x-3) \cdot \sqrt{\dfrac{x}{(x-2)^3}}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-0279c862e930b2824bfd34631b7eaa8b_l3.png)
Torej,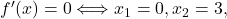 kar pomeni, da sta točki
kar pomeni, da sta točki 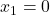 in
in 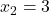 stacionarni točki.
stacionarni točki. - V naslednji tabeli bomo povzeli vse podatke, ki smo jih pridobili v prejšnjih točkah, in ugotovili intervale naraščanja oziroma padanja funkcije
 .
.
Funkcija narašča na intervalu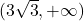 ter pada na uniji intervalov
ter pada na uniji intervalov ![Rendered by QuickLaTeX.com (-\infty, 0]\cup (2,3)](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-86abeeefc0c249f819daae1e4ad06af2_l3.png) . Točki
. Točki  in
in  sta lokalna minimuma. Razvidno je, da je v točki
sta lokalna minimuma. Razvidno je, da je v točki  globalni minimum dane funkcije
globalni minimum dane funkcije  .
. - Graf funkcije je na sliki 21.11.
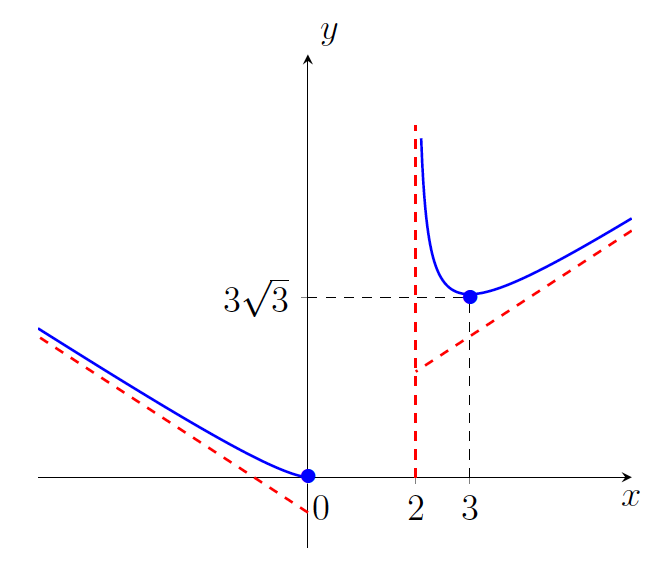
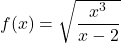 .
.Z grafa funkcije razberemo, da je funkcija vedno konveksna.
Naloga 19: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]()
Rešitev:
- Logaritemska funkcija je definirana tam, kjer je njen argument večji od
 ; v tem primeru moramo imeti
; v tem primeru moramo imeti 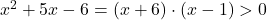 . Rešimo neenačbo ob pomoči naslednje tabele.
. Rešimo neenačbo ob pomoči naslednje tabele.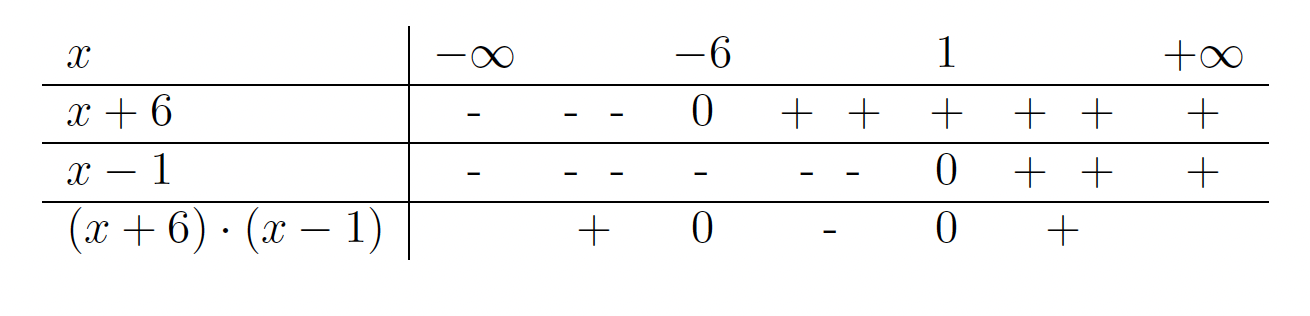
Dobimo, da je domena funkcije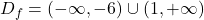 .
. - Ničle funkcije
 so rešitve enačbe
so rešitve enačbe 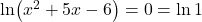 oziroma
oziroma 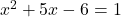 , kar pomeni
, kar pomeni 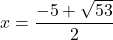 in
in 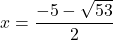 . Obe točki pripadata domeni, torej sta ničli dane funkcije.
. Obe točki pripadata domeni, torej sta ničli dane funkcije.
Funkcija nima niti polov niti navpičnih asimptot. - Poiščimo vse eventualne vodoravne ali poševne asimptote. Najprej izračunamo limiti dane funkcije, ko gre
 proti
proti 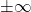 , in dobimo
, in dobimo 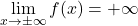 , torej funkcija nima vodoravnih asimptot. Da bi se prepričali, ali ima poševne asimptote, nato izračunamo še limito
, torej funkcija nima vodoravnih asimptot. Da bi se prepričali, ali ima poševne asimptote, nato izračunamo še limito
![Rendered by QuickLaTeX.com \[\lim_{x\to \pm\infty} \dfrac{f(x)}{x}\stackrel{\left[\frac{\infty}{\infty}\right]}{\underset{\text{L'H}}{=}} \lim_{x\to \pm\infty} \dfrac{\dfrac{2x+5}{x^2+5x-6}}{1}=0.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-6a207ad4eb70d212a40734b6965d5a9f_l3.png)
To pomeni, da poševna asimptota ne obstaja.
Izračunamo še enostranski limiti na robovih definicijskega območja:![Rendered by QuickLaTeX.com \[\lim_{x\to 1^+} f(x)&= \ln 0^+=-\infty\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-fc0348061676e0e641f181fa53d3ed2a_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x\to -6^-} f(x)&= \ln 0^+=-\infty.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-58b78acd308a4d7d4a1452b0a0628f95_l3.png)
- Stacionarne točke so ničle prvega odvoda, ki ima predpis
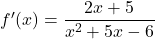 in edino ničlo
in edino ničlo 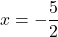 , ki pa ne pripada domeni
, ki pa ne pripada domeni  . To pomeni, da funkcija nima ekstremov.
. To pomeni, da funkcija nima ekstremov. - Ob pomoči naslednje tabele ugotovimo intervale naraščanja oziroma padanja funkcije
 .
. Funkcija narašča na intervalu
Funkcija narašča na intervalu  ter pada na intervalu
ter pada na intervalu 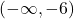 .
. - Graf funkcije je na sliki 21.12.
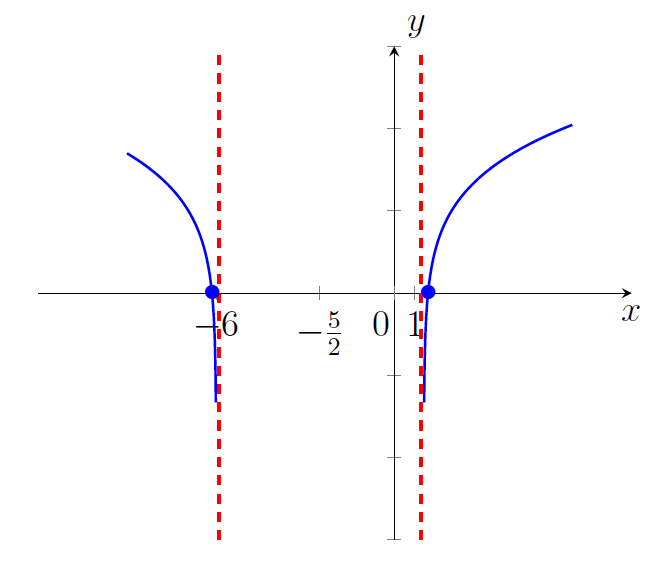

Naloga 20: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]()
Rešitev:
- Dana funkcija je produkt med linearno funkcijo
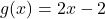 in eksponentno funkcijo
in eksponentno funkcijo 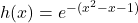 . Ker sta obe funkciji povsod definirani, je domena funkcije
. Ker sta obe funkciji povsod definirani, je domena funkcije  torej
torej 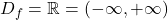 .
. - Eksponentna funkcija ni nikoli enaka
 , torej so ničle funkcije ničle linearne funkcije
, torej so ničle funkcije ničle linearne funkcije 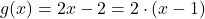 oziroma
oziroma  .
.
Funkcija nima niti polov niti navpičnih asimptot. - Poiščimo vse eventualne vodoravne ali poševne asimptote.
Zdaj izračunamo limite dane funkcije, ko gre proti
proti 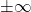 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} f(x) &= \lim_{x \to -\infty} (2x-2)\cdot e^{-(x^2-x-1)} = \lim_{x \to -\infty} \dfrac{2x-2}{e^{x^2-x-1}}\stackrel{[\frac{-\infty}{\infty}]}{\underset{\text{L'H}}{=}}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-9b9f8433106ee707011edda68944b5b0_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x \to -\infty} \dfrac{2}{(2x-1)\cdot e^{x^2-x-1}}=\dfrac{2}{-\infty}=0^-\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-05b696b923020467346d70f86eeaa1f4_l3.png)
in podobno
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} f(x) &= \lim_{x \to +\infty} (2x-2)\cdot e^{-(x^2-x-1)} = \lim_{x \to +\infty} \dfrac{2x-2}{e^{x^2-x-1}}\stackrel{[\frac{+\infty}{\infty}]}{\underset{\text{L'H}}{=}}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-d1ee175a12bc5879d981995ba7b8d917_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x \to +\infty} \dfrac{2}{(2x-1)\cdot e^{x^2-x-1}}=\dfrac{2}{+\infty}=0^+,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-410a0bce1711b3234dc54086263ba665_l3.png)
torej je premica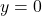 vodoravna asimptota, kar pomeni, da funkcija nima poševnih asimptot.
vodoravna asimptota, kar pomeni, da funkcija nima poševnih asimptot. - Poiščimo stacionarne točke oziroma ničle prvega odvoda:
![Rendered by QuickLaTeX.com \[f'(x) =& 2\cdot e^{-x^2+x+1}+(2x-2)\cdot e^{-x^2+x+1}\cdot (-2x+1)\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-7cfda338099fcd057489030a3c11e080_l3.png)
![Rendered by QuickLaTeX.com \[=e^{-x^2+x+1}\cdot [2+(2x-2)\cdot (-2x+1)]=e^{-x^2+x+1}\cdot (-4x^2+6x).\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-8e805bbbae5491e0747f0475c17b9b4d_l3.png)
Ker je
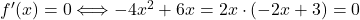 , sta
, sta  in
in 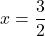 stacionarni točki.
stacionarni točki. - Ob pomoči tabele 21.2 identificiramo intervale naraščanja oziroma padanja ter intervale konveksnosti oziroma konkavnosti. Predznak prvega odvoda
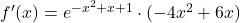 je enak predznaku kvadratne funkcije
je enak predznaku kvadratne funkcije 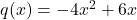 , ki ima graf parabole na sliki 21.13.
, ki ima graf parabole na sliki 21.13.
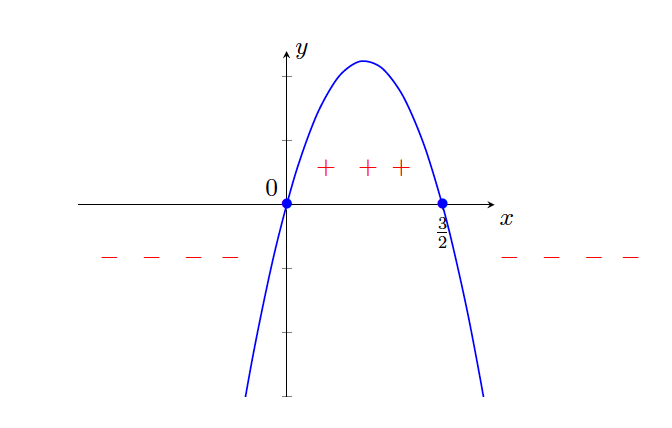
21.13: Graf kvadratne funkcije 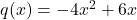 .
.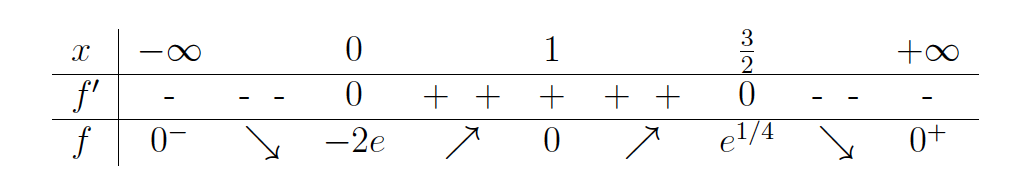
Tabela 21.2: Intervali naraščanja in padanja funkcije 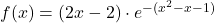 .
.Ugotovimo, da je funkcija
 naraščajoča na intervalu
naraščajoča na intervalu ![Rendered by QuickLaTeX.com [0,\dfrac{3}{2}]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-a6bc905aee75b5fefec2993b7f454557_l3.png) ter padajoča na uniji intervalov
ter padajoča na uniji intervalov ![Rendered by QuickLaTeX.com (-\infty, 0]\cup [\dfrac{3}{2}, +\infty)](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-e38a7e7ec27e9d867a03d4669137e920_l3.png) . Pri
. Pri  ima funkcija lokalni minimum, pri
ima funkcija lokalni minimum, pri 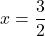 pa lokalni maksimum.
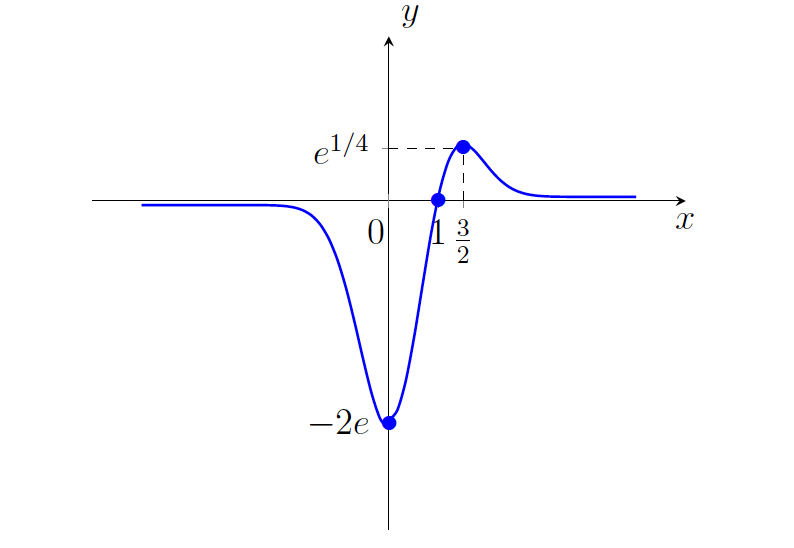
pa lokalni maksimum. - Na podlagi prejšnje tabele bomo narisali graf funkcije
 (glej sliko 21.14).
(glej sliko 21.14).
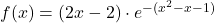 .
.
Naloga 21: Skicirajmo graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]() na intervalu
na intervalu ![]() .
.
Rešitev:
- Dana funkcija je definirana tam, kjer je imenovalec različen od
 , torej tam, kjer je
, torej tam, kjer je 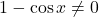 oziroma
oziroma 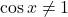 ekvivalentno
ekvivalentno 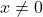 in
in 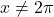 . Dobimo, da je domena
. Dobimo, da je domena 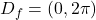 .
. - Ničle funkcije so ničle števca. Ker je
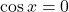 na
na 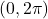 za
za 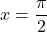 in
in 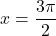 , sklepamo, da sta ničli funkcije
, sklepamo, da sta ničli funkcije 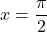 in
in 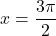 .
. - Funkcija ima dva pola, v točkah
 in
in 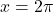 , kjer ima tudi navpični asimptoti. Nima pa vodoravnih ali poševnih asimptot.
, kjer ima tudi navpični asimptoti. Nima pa vodoravnih ali poševnih asimptot.
Ker je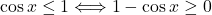 , dobimo, da je
, dobimo, da je
![Rendered by QuickLaTeX.com \[\lim_{x \to 0^+} (1-\cos x)=0^+= \lim_{x \to 2\pi^-} (1-\cos x),\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-c2677cf9f883246a70c4a95b3aa11196_l3.png)
in zato je
![Rendered by QuickLaTeX.com \[\lim_{x \to 0^+} f(x)=\dfrac{1}{0^+}=+\infty=\lim_{x \to 2\pi^-} f(x).\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-3c457b8789f0b5d50cea8ac14549e7e6_l3.png)
- Poiščimo stacionarne točke oziroma ničle prvega odvoda:
![Rendered by QuickLaTeX.com \[f'(x) =\dfrac{-\sin x\cdot (1-\cos x)-\cos x\cdot \sin x}{(1-\cos x)^2}=\dfrac{-\sin x}{(1-\cos x)^2}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-28c0c14a00cc239824278e04855bf412_l3.png)
Ker je
 , je
, je 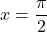 stacionarna točka funkcije
stacionarna točka funkcije  . Poiščemo še prevoje oziroma ničle drugega odvoda:
. Poiščemo še prevoje oziroma ničle drugega odvoda:
![Rendered by QuickLaTeX.com \[f''(x)&=\dfrac{-\cos x\cdot (1-\cos x)^2-(-\sin x)\cdot 2\cdot (1-\cos x)\cdot \sin x}{(1-\cos x)^4}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-24c77fc6b42db7a16a9a985310ae75c7_l3.png)
![Rendered by QuickLaTeX.com \[=\dfrac{(1-\cos x)\cdot [-\cos x\cdot (1-\cos x)+2\sin^2 x]}{(1-\cos x)^4}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-b3931b9e1f2c6afa8e6ce1b75daa985c_l3.png)
![Rendered by QuickLaTeX.com \[=\dfrac{\cos^2 x-\cos x+2\cdot (1-\cos^2 x)}{(1-\cos x)^3}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-cdeba55fdd214eb318dded20e94ca76b_l3.png)
![Rendered by QuickLaTeX.com \[=\dfrac{2-\cos x-\cos^2 x}{(1-\cos x)^3}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-c6da886dfdc475ed4a83cf0ac435ce1e_l3.png)
![Rendered by QuickLaTeX.com \[=\dfrac{(1-\cos x)\cdot(2+\cos x)}{(1-\cos x)^3}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-e575896e3cf131f4a9cf1401c81e5b91_l3.png)
![Rendered by QuickLaTeX.com \[=\dfrac{2+\cos x}{(1-\cos x)^2}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-0da4024d65dcb616558115995a90d18d_l3.png)
Dobimo, da je , torej funkcija nima prevoja.
, torej funkcija nima prevoja. - Identificiramo intervale naraščanja oziroma padanja ter intervale konveksnosti oziroma konkavnosti.
Ker je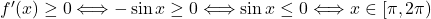 , ugotovimo, da je funkcija naraščajoča na intervalu
, ugotovimo, da je funkcija naraščajoča na intervalu 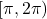 ter padajoča na intervalu
ter padajoča na intervalu ![Rendered by QuickLaTeX.com (0, \pi]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-7bc16cb286cf87ca1cdd59587cd2c705_l3.png) .
.
Ker je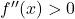 za vsak
za vsak  v domeni, je funkcija
v domeni, je funkcija  povsod konveksna.
povsod konveksna. - Zdaj skiciramo graf funkcije
 (slika 21.15).
(slika 21.15).
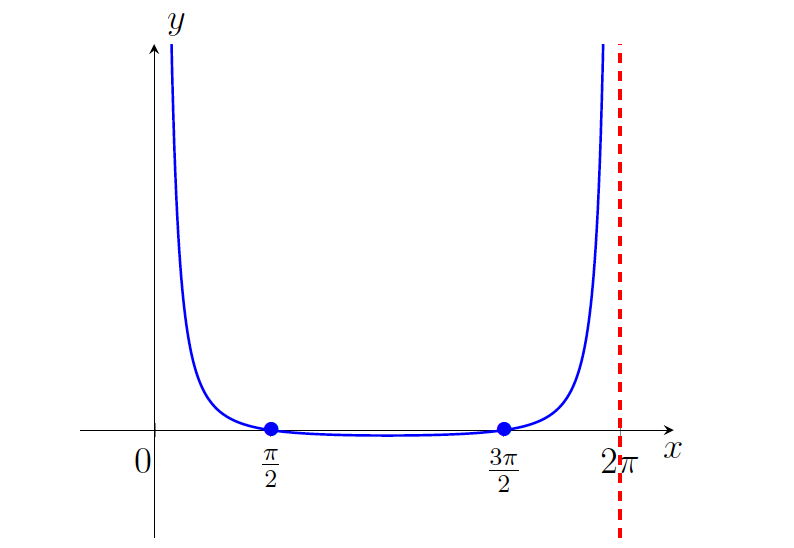
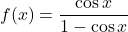 na intervalu
na intervalu ![Rendered by QuickLaTeX.com [0, 2\pi]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-ab5ce0577e8cf8aeb6bfb6e0c0488382_l3.png) .
.Naloga 22: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]() in definirane na intervalu
in definirane na intervalu ![]() .
.
Rešitev:
- Po navodilu je domena funkcije
 taka:
taka: ![Rendered by QuickLaTeX.com D_f=[0, 2\pi]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-60b112435259cd4842a0f49021422780_l3.png) .
. - Ničle funkcije so rešitve enačbe
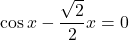 . Ker jih ni mogoče dobiti z metodami, ki jih poznamo, bomo to točko preskočili.
. Ker jih ni mogoče dobiti z metodami, ki jih poznamo, bomo to točko preskočili. - Funkcija je podana kot razlika med funkcijo kosinusa in linearno funkcijo, torej nima polov, nima navpičnih asimptot in niti vodoravnih ali poševnih asimptot.
- Poiščimo stacionarne točke in lokalne ekstreme. Izračunamo vrednost prvega odvoda in dobimo
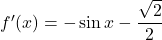 , obstaja povsod na intervalu
, obstaja povsod na intervalu 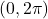 . Znotraj tega odprtega intervala je
. Znotraj tega odprtega intervala je
![Rendered by QuickLaTeX.com \[f'(x) = -\sin x - \frac{\sqrt{2}}{2} = 0 \Longleftrightarrow \sin x = - \frac{\sqrt{2}}{2},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-e7170ecd932c1bbcc6be5d72bd9e29bb_l3.png)
zato sta stacionarni točki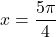 in
in 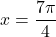 .
.
Vrednost drugega odvoda je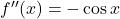 , in ker je
, in ker je 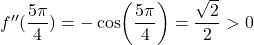 , sledi, da ima funkcija lokalni minimum v točki
, sledi, da ima funkcija lokalni minimum v točki 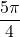 . Podobno je
. Podobno je 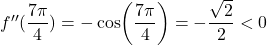 , kar pomeni, da ima funkcija lokalni maksimum v točki
, kar pomeni, da ima funkcija lokalni maksimum v točki 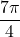 .
.
Funkcija narašča, ko je
narašča, ko je 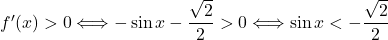 , torej ko je
, torej ko je 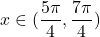 . Funkcija pada za
. Funkcija pada za  .
. - Prevoji funkcije so ničle drugega odvoda oziroma rešitve enačbe
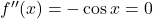 . Dobimo prevoja
. Dobimo prevoja 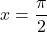 in
in 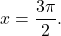 Vidimo, da je funkcija konveksna na intervalu
Vidimo, da je funkcija konveksna na intervalu 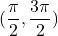 , ko je
, ko je  . Funkcija
. Funkcija  je konkavna na uniji intervalov
je konkavna na uniji intervalov 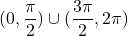 .
.
Ovrednotimo še funkcijo na robovih domene in dobimo
na robovih domene in dobimo 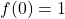 in
in 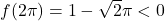 .
. - V naslednji tabeli bomo povzeli vse podatke, ki smo jih pridobili v prejšnjih točkah, in ugotovili intervale naraščanja oziroma padanja ter konveksnosti oziroma konkavnosti funkcije
 .
.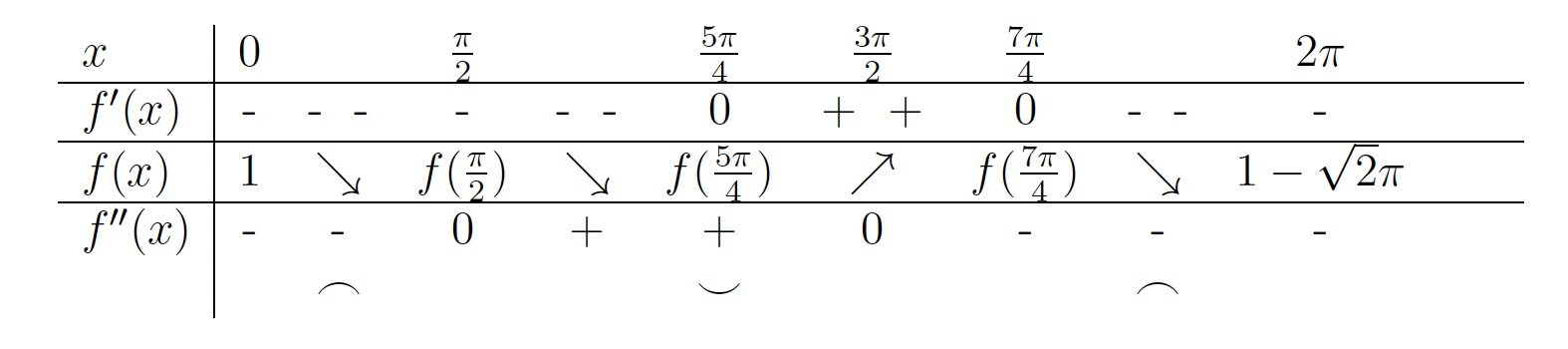
- Zdaj skiciramo graf dane funkcije na sliki 21.16.
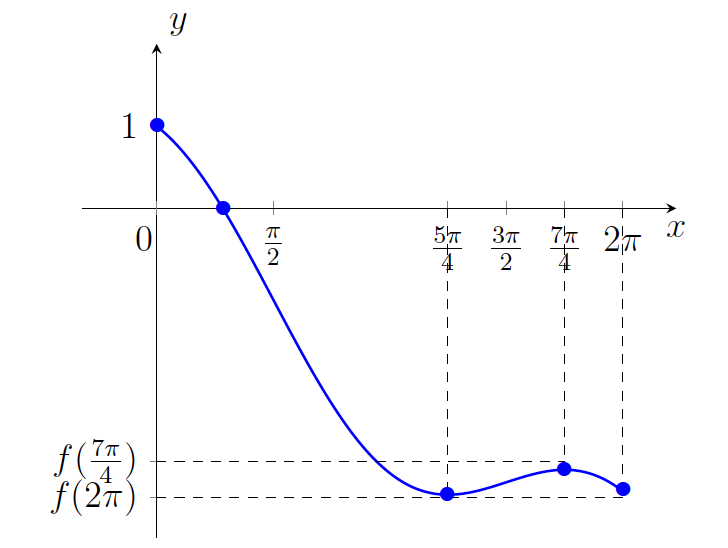
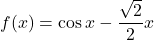 na intervalu
na intervalu ![Rendered by QuickLaTeX.com [0, 2\pi]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-ab5ce0577e8cf8aeb6bfb6e0c0488382_l3.png) .
.Naloga 23: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]()
Rešitev:
- Kvadratni koren je dobro definiran, ko je njegov argument pozitiven, zato je prvi pogoj za domeno
![Rendered by QuickLaTeX.com x^2-1\geq 0\Longleftrightarrow x\in (-\infty, -1]\cup [1, +\infty)](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-1b28235b982b3ed3a4976884e36fab3d_l3.png) . Drugi pogoj pravi, da mora biti imenovalec različen od
. Drugi pogoj pravi, da mora biti imenovalec različen od  , torej
, torej 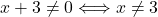 . Dobimo, da je domena funkcije
. Dobimo, da je domena funkcije ![Rendered by QuickLaTeX.com D_f=(-\infty, -3)\cup (-3, -1]\cup [1, +\infty)](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-bfa115c6abb444d03b1292c63dbdf290_l3.png) .
. - Ničle funkcije so ničle števca, torej
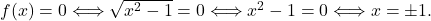
- Funkcija ima samo en pol, tj. ničla imenovalca
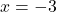 in premica
in premica 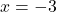 je navpična asimptota dane funkcije. Izračunamo še enostranski limiti v točki
je navpična asimptota dane funkcije. Izračunamo še enostranski limiti v točki 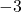 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to -3^+} f(x) = \lim_{x \to -3^+} \frac{\sqrt{8}}{0^+} = +\infty,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-1ba1bd9646ce07070e7cd39a61dc7e65_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x \to -3^-} f(x) = \lim_{x \to -3^-} \frac{\sqrt{8}}{0^-} = -\infty.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-d19286814e6b9c7b39e3a2dda274aa9b_l3.png)
- Poiščimo vse druge eventualne asimptote.
I) Zdaj izračunamo limite dane funkcije, ko gre proti
proti 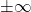 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} f(x) &= \lim_{x \to -\infty} \dfrac{\sqrt{x^2\cdot \left(1-\dfrac{1}{x^2}\right)}}{x\cdot \left(1+\dfrac{3}{x}\right)}=\lim_{x \to -\infty} \dfrac{\lvert x\rvert\cdot \sqrt{1-\dfrac{1}{x^2}}}{x\cdot \left(1+\dfrac{3}{x}\right)}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-d097fba4a9d0a8883bab97ae40eca87f_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x \to -\infty} \dfrac{-x\cdot \sqrt{1-\boxed{\frac{1}{x^2}}_{\searrow 0}}}{x\cdot \left(1+\boxed{\frac{3}{x}}_{\searrow 0}\right)}=-1,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-561765665a4862bf1af81c4ac7f488b4_l3.png)
kar pomeni, da je premica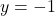 vodoravna asimptota funkcije
vodoravna asimptota funkcije  , ko gre
, ko gre  proti
proti  .
.
Podobno izračunamo
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} f(x) &= \lim_{x \to +\infty} \dfrac{\sqrt{x^2\cdot \left(1-\dfrac{1}{x^2}\right)}}{x\cdot \left(1+\dfrac{3}{x}\right)}=\lim_{x \to +\infty} \dfrac{\lvert x\rvert\cdot \sqrt{1-\dfrac{1}{x^2}}}{x\cdot \left(1+\dfrac{3}{x}\right)}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-607281591d4f3bd4abaaf49de477eacd_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x \to +\infty} \dfrac{x\cdot \sqrt{1-\boxed{\frac{1}{x^2}}_{\searrow 0}}}{x\cdot \left(1+\boxed{\frac{3}{x}}_{\searrow 0}\right)}=1,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-40a0b06cfd0b13ea0d310fff7f5bf620_l3.png)
torej je premica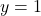 vodoravna asimptota funkcije
vodoravna asimptota funkcije  , ko gre
, ko gre  proti
proti 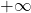 .
.
II) Funkcija nima poševnih asimptot, ker ima vodoravno asimptoto pri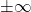 .
. - Stacionarne točke so ničle prvega odvoda, ki ima obliko:
![Rendered by QuickLaTeX.com \[f'(x) &=\dfrac{\dfrac{2x}{2\sqrt{x^2-1}}\cdot (x+3)-\sqrt{x^2-1}\cdot 1}{(x+3)^2} = \dfrac{x\cdot (x+3)- (x^2-1)}{\sqrt{x^2-1}\cdot (x+3)^2}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-c9579ec273d0708e3c332f5280b380f7_l3.png)
![Rendered by QuickLaTeX.com \[= \dfrac{3x+1}{\sqrt{x^2-1}\cdot (x+3)^2}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-f7234f70fb374d261d660b4854908258_l3.png)
Torej, natanko tedaj, ko je
natanko tedaj, ko je  , ki pa ne pripada domeni. To pomeni, da funkcija nima stacionarnih točk.
, ki pa ne pripada domeni. To pomeni, da funkcija nima stacionarnih točk. - V naslednji tabeli bomo povzeli vse podatke, ki smo jih pridobili v prejšnjih točkah, in ugotovili intervale naraščanja oziroma padanja funkcije
 .
. Funkcija
Funkcija  narašča na intervalu
narašča na intervalu 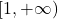 ter pada na
ter pada na ![Rendered by QuickLaTeX.com (-\infty, -3)\cup (-3,-1]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-3d4fb072e2705ac63fff1839270dd238_l3.png) .
. - Graf funkcije je na sliki 21.17.
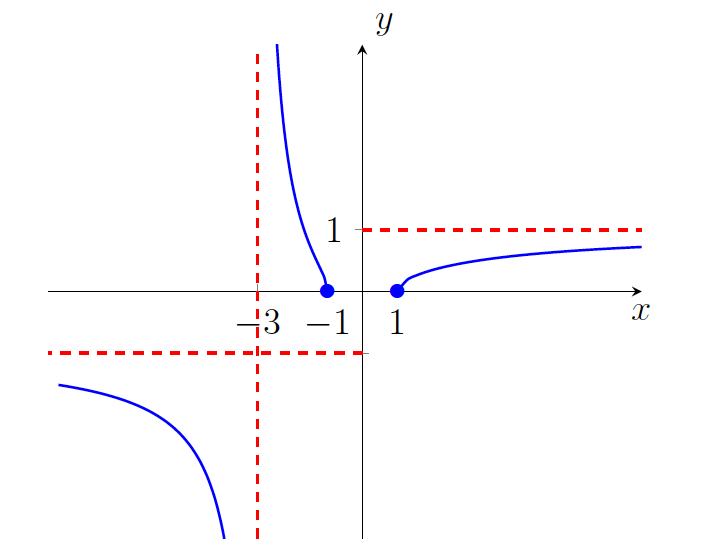
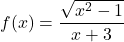 .
.Z grafa funkcije razberemo, da je funkcija konveksna na intervalu ![]() ter konkavna na uniji intervalov
ter konkavna na uniji intervalov ![]() .
.
Naloga 24: Skicirajte graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]()
Rešitev:
- Argument korenske funkcije s sodim korenskim eksponentom mora biti pozitiven, torej moramo imeti
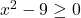 , kar vpliva na to, da je domena funkcije
, kar vpliva na to, da je domena funkcije  enaka
enaka ![Rendered by QuickLaTeX.com D_f=(-\infty, -3]\cup [3, +\infty)](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-10647db921fb45bf8ce5f2c68e5fcd93_l3.png) .
. - Ničle funkcije so rešitve enačbe
![Rendered by QuickLaTeX.com \[f(x) = 0 \Longleftrightarrow \sqrt{x^2-9}-x=0 \Longleftrightarrow \sqrt{x^2-9}=x.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-451f274f93afdba6ddfd71920f3c3925_l3.png)
Če enačbo kvadriramo, dobimo
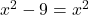 , a ta nima rešitev. Zato dana funkcija nima ničel.
, a ta nima rešitev. Zato dana funkcija nima ničel. - Funkcija nima niti polov niti navpičnih asimptot.
- Poiščimo vse druge eventualne asimptote.
I) Najprej izračunamo limito dane funkcije v
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} (\sqrt{x^2-9}-x)= +\infty-(-\infty)=+\infty,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-c4d08304fd562e3d900aa30418832732_l3.png)
kar pomeni, da funkcija nima vodoravne asimptote v .
.
Zdaj izračunamo limito funkcije v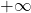 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} f(x) &= \lim_{x \to +\infty} (\sqrt{x^2-9}-x)\stackrel{[\infty-\infty]}{=}\lim_{x \to +\infty} \dfrac{\left(\sqrt{x^2-9}-x\right)\cdot \left(\sqrt{x^2-9}+x\right)}{\sqrt{x^2-9}+x}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-0951f0d5a1e129859b577056db148eeb_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x \to +\infty} \dfrac{x^2-9-x^2}{\sqrt{x^2-9}+x}=-\dfrac{9}{+\infty}=0^-.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-24a50b871696c120165371dbc2950112_l3.png)
Torej, premica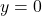 je vodoravna asimptota funkcije v
je vodoravna asimptota funkcije v 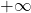 , kjer funkcija zagotovo nima poševnih asimptot.
, kjer funkcija zagotovo nima poševnih asimptot.
II) Preverimo, ali ima funkcija poševno asimptoto pri .
.
Najprej izračunamo limito
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} \dfrac{f(x)}{x} &= \lim_{x \to -\infty} \dfrac{\sqrt {x^2-9}-x}{x}\stackrel{[\frac{\infty}{\infty}]}{\underset{\text{L'H}}{=}}\lim_{x \to -\infty} \dfrac{\dfrac{2x}{2\sqrt{x^2-9}}-1}{1}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4a41e30db6d05155e74ac123946d1048_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x \to -\infty}\left(\dfrac{x}{\sqrt{x^2\cdot \left(1-\dfrac{9}{x^2}\right)}}-1\right)\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-e0b9f4a9c335b2ae6391d1ceee522af9_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x \to -\infty} \left( \dfrac{x}{-x\cdot \sqrt{1-\boxed{\frac{9}{x^2}}_{\searrow 0}}}-1\right)=-2=m\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-d861724959a34f9783f05f8b8aa174f0_l3.png)
in zdaj drugo limito
![Rendered by QuickLaTeX.com \[q=\lim_{x \to -\infty} [f(x) - mx] = \lim_{x \to -\infty} \left(\sqrt{x^2-9} - x+2x\right)\stackrel{[\infty-\infty]}{=}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-28ca73e80c77977d9b449090bd3202b4_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} \left(\sqrt{x^2-9}+ x\right) \cdot \dfrac{\sqrt{x^2-9}-x}{\sqrt{x^2-9}-x}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-50eecff532feb8700e278de80a34c0f7_l3.png)
![Rendered by QuickLaTeX.com \[=\lim_{x \to -\infty} \dfrac{x^2-9-x^2}{\sqrt{x^2-9}-x} =\dfrac{-9}{+\infty-(-\infty)}=0^-.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-96ea300b008951c7122dcd760c313926_l3.png)
Premica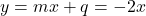 je torej poševna asimptota funkcije
je torej poševna asimptota funkcije  pri
pri 
- Stacionarne točke so ničle prvega odvoda:
![Rendered by QuickLaTeX.com \[f'(x) =\dfrac{2x}{2\sqrt{x^2-9}}-1=\dfrac{x-\sqrt{x^2-9}}{\sqrt{x^2-9}}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-0d722c6de654a8ce3e22b86c11f8acc8_l3.png)
Za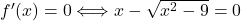 že vemo, da nima rešitev. Sledi, da funkcija nima stacionarnih točk.
že vemo, da nima rešitev. Sledi, da funkcija nima stacionarnih točk.
Preučimo predznak prvega odvoda funkcije . Ker je števec prvega odvoda funkcije
. Ker je števec prvega odvoda funkcije  vedno pozitiven (upoštevajte, da je to kvadratni koren), je predznak odvoda podan s predznakom imenovalca. Domena dane funkcije je
vedno pozitiven (upoštevajte, da je to kvadratni koren), je predznak odvoda podan s predznakom imenovalca. Domena dane funkcije je ![Rendered by QuickLaTeX.com D_f=(-\infty, -3]\cup [3, +\infty)](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-10647db921fb45bf8ce5f2c68e5fcd93_l3.png) .
.
a) Če je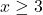 , neenačbo
, neenačbo 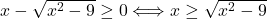 kvadriramo in dobimo
kvadriramo in dobimo 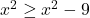 oziroma
oziroma 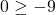 , kar je vedno pravilno. To pomeni, da za
, kar je vedno pravilno. To pomeni, da za 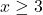 je
je 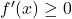 , zato je funkcija
, zato je funkcija  naraščajoča.
naraščajoča.
b) Če je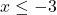 , dobimo, da je
, dobimo, da je 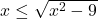 (prva stran neenačbe je negativna, druga pa je pozitivna, torej je neenačba pravilna), kar pomeni, da je
(prva stran neenačbe je negativna, druga pa je pozitivna, torej je neenačba pravilna), kar pomeni, da je 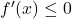 oziroma funkcija pada na intervalu
oziroma funkcija pada na intervalu ![Rendered by QuickLaTeX.com (-\infty, -3]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-ad44d0a9d1baef350f18fc17ea25a15f_l3.png) .
. - V naslednji tabeli bomo povzeli vse podatke, ki smo jih pridobili v prejšnjih točkah.

- Graf funkcije je narisan na sliki 21.18.
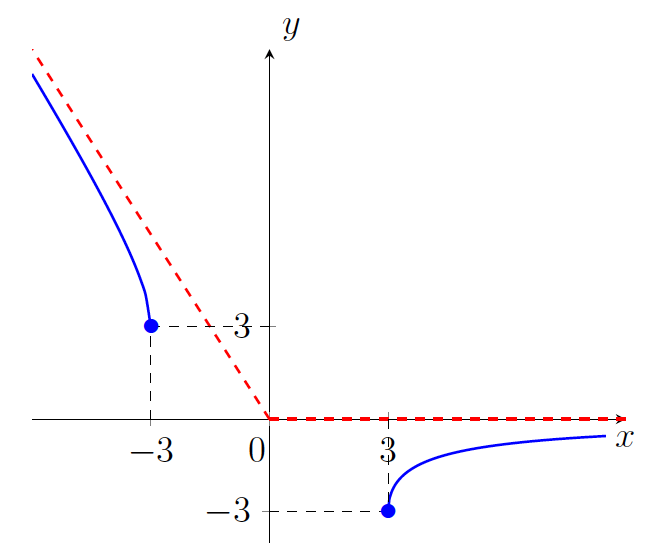
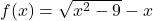 .
.
Z grafa funkcije razberemo, da je funkcija vedno konkavna.