2 Obratna (inverzna) matrika (I)
Definicija 2.1: Naj bo 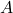 kvadratna matrika reda
kvadratna matrika reda  . Inverzna matrika (obratna matrika ali inverz) matrike
. Inverzna matrika (obratna matrika ali inverz) matrike 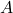 (oznaka
(oznaka 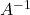 ) je takšna matrika, za katero velja
) je takšna matrika, za katero velja 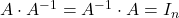 . Če obstaja inverzna matrika, je
. Če obstaja inverzna matrika, je 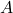 obrnljiva matrika.
obrnljiva matrika.
Ena matrika ima lahko kvečjemu en inverz in ničelna matrika seveda nima inverza.
Primer 2.1: Naj bo ![]() in
in ![]() . Izračunamo produkt
. Izračunamo produkt
![]()
Podobno je ![]() . Torej, matriki
. Torej, matriki ![]() in
in ![]() sta obrnljivi in
sta obrnljivi in ![]() je inverz matrike
je inverz matrike ![]() , tj.
, tj. ![]() , in
, in ![]() je inverz matrike
je inverz matrike ![]() , tj.
, tj. ![]() .
.
Lastnosti inverzne matrike: Naj bosta ![]() in
in ![]() obrnljivi matriki reda
obrnljivi matriki reda ![]() ter
ter ![]() skalar. Potem velja:
skalar. Potem velja:
-
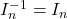 ;
; 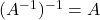 ;
;-
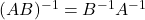 ;
; -
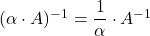 ;
; -
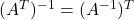 .
.
V razdelku 4. bomo predstavili, kako izračunamo inverz matrike.