3 Determinanta matrike
1. Osnovni pojmi
V tem poglavju bomo preučili pojem determinante kvadratne matrike, ki nam pomaga ugotoviti, ali je določena matrika obrnljiva ali ne. Poleg tega z determinantami lahko izračunamo inverzno matriko ter rešimo sisteme linearnih enačb.
Definicija 3.1: Determinanta kvadratne matrike ![]() reda
reda ![]() je število
je število ![]() , ki ga rekurzivno izračunamo z naslednjima praviloma:
, ki ga rekurzivno izračunamo z naslednjima praviloma:
- Če je
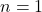 , tedaj je determinanta matrike
, tedaj je determinanta matrike 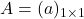 enaka
enaka 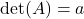 .
. - Če je
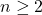 , determinanto matrike
, determinanto matrike
![Rendered by QuickLaTeX.com \[A= \begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n}\\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots & \vdots & \ldots & \vdots\\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{pmatrix}_{n \times n}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-f15708f005b35afb83f966c68cae168a_l3.png)
izračunamo po pravilu
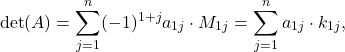
kjer je ![]() determinanta podmatrike, ki jo dobimo tako, da izpustimo prvo vrstico in
determinanta podmatrike, ki jo dobimo tako, da izpustimo prvo vrstico in ![]() -ti stolpec iz matrike
-ti stolpec iz matrike ![]() . Elementu
. Elementu ![]() pravimo kofaktor elementa
pravimo kofaktor elementa ![]() v matriki
v matriki ![]() . Ta formula se imenuje razvoj determinante po prvi vrstici.
. Ta formula se imenuje razvoj determinante po prvi vrstici.
Primer 3.1: Izračunajmo determinanto matrike ![]()
Z razvojem po prvi vrstici dobimo
![]()
Po istem pravilu lahko izračunamo splošno determinanto ![]() :
:
![]()
Primer 3.2: Poiščimo determinanto matrike 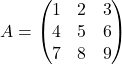 .
.
Najprej izberemo prvo vrstico in izračunamo:
![Rendered by QuickLaTeX.com \[\begin{array}{lll} \det(A)&=& (-1)^{1+1}\cdot 1\cdot \begin{vmatrix} 5 & 6\\ 8 & 9 \end{vmatrix} +(-1)^{1+2}\cdot 2\cdot \begin{vmatrix} 4 & 6\\ 7 & 9 \end{vmatrix} + (-1)^{1+3}\cdot 3\cdot \begin{vmatrix} 4& 5\\ 7 & 8 \end{vmatrix} =\\ &=&1\cdot (5\cdot 9-6\cdot 8)-2\cdot (4\cdot 9-6\cdot 7)+3\cdot (4\cdot 8-5\cdot 7)=0. \end{array}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-2a8fcf324ff91578f1c2d767b1fff004_l3.png)
Izrek 3.1 [1,5]: Determinanto lahko izračunamo tudi z razvojem po kaki drugi vrstici.
Razvoj po ![]() -ti vrstici je
-ti vrstici je
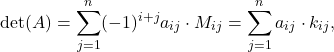
kjer je ![]() determinanta podmatrike, ki jo dobimo tako, da izpustimo
determinanta podmatrike, ki jo dobimo tako, da izpustimo ![]() -to vrstico in
-to vrstico in ![]() -ti stolpec iz matrike
-ti stolpec iz matrike ![]() ; elementu
; elementu ![]() pravimo kofaktor elementa
pravimo kofaktor elementa ![]() v matriki
v matriki ![]() ,
, ![]() .
.
 , podane v Primeru 3.2:
, podane v Primeru 3.2: ![Rendered by QuickLaTeX.com \[\begin{array}{lll} \det(A)&=& (-1)^{2+1}\cdot 4\cdot \begin{vmatrix} 2 & 3\\ 8 & 9 \end{vmatrix} +(-1)^{2+2}\cdot 5\cdot \begin{vmatrix} 1 & 3\\ 7 & 9 \end{vmatrix} + (-1)^{2+3}\cdot 6\cdot \begin{vmatrix} 1& 2\\ 7 & 8 \end{vmatrix} =\\ &=&(-4)\cdot (2\cdot 9-3\cdot 8)+5\cdot (1\cdot 9-3\cdot 7)-6\cdot (1\cdot 8-2\cdot 7)=0. \end{array}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-9e2b1fe2abdba85b0f280613bf7930ef_l3.png)
Vrednost determinante se ne spremeni, če vlogi vrstic in stolpcev zamenjamo. Torej dobimo naslednji izrek.
Izrek 3.2 [1,5]: Determinanti matrike in njene transponiranke sta enaki: ![]() .
.
Na podlagi te lastnosti lahko izračunamo determinanto z razvojem po poljubni vrstici ali stolpcu. Običajno bomo izbrali tisto vrstico ali stolpec, ki ima več ničel, saj bomo v vsoti dobili več členov, enakih nič, in zato bo izračun determinante hitrejši.
Primer 3.4: Izračunajmo determinanto matrike 
V tem primeru izberemo tretji stolpec, ker ima determinanta v tem stolpcu vse elemente razen enega enake ![]() , in dobimo
, in dobimo
![Rendered by QuickLaTeX.com \[\det(A)= 1\cdot (-1)^{2+3}\begin{vmatrix} 1& 3 & 4\\ 1 & 1&3\\ 2& -1& 1\end{vmatrix}=\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-f086f124b0ce4c8323d472ee42faac4a_l3.png)
in zdaj nadaljujemo z razvojem determinante ![]() po drugi vrstici:
po drugi vrstici:
![]()
![]()
Primer 3.5: Izračunajmo determinanto matrike  .
.
S ponavljanjem razvoja determinante po prvi vrstici dobimo
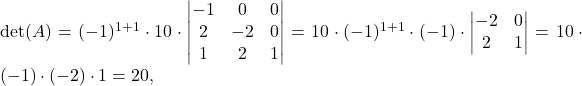
torej je vrednost determinante enaka produktu diagonalnih elementov.
Podobno velja za matriko 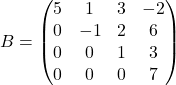 . Njena determinanta je
. Njena determinanta je
![]()
Kvadratna matrika, ki ima vse elemente pod glavno diagonalo enake ![]() , se imenuje zgornje trikotna matrika, če ima vse elemente nad glavno diagonalo enake
, se imenuje zgornje trikotna matrika, če ima vse elemente nad glavno diagonalo enake ![]() , pa spodnje trikotna matrika. Determinanta zgornje oziroma spodnje trikotne matrike je enaka produktu diagonalnih elementov.
, pa spodnje trikotna matrika. Determinanta zgornje oziroma spodnje trikotne matrike je enaka produktu diagonalnih elementov.
2. Lastnosti determinant
Naj bo ![]() poljubna kvadratna matrika reda
poljubna kvadratna matrika reda ![]() . Velja [1,5]:
. Velja [1,5]:
- Determinanti matrike in njene transponiranke sta enaki, kar pomeni, da je
![Rendered by QuickLaTeX.com \[\det(A) = \det(A^T).\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-e07c4a7d54cd8866dd1b73702a55d484_l3.png)
- Če ena vrstica ali en stolpec matrike vsebuje same ničle, je njena determinanta enaka
 .
.
Na primer,![Rendered by QuickLaTeX.com \[\begin{vmatrix} 1& 2 & 3 \\ 0 & 0 & 0 \\ 7 & 8 & 9 \end{vmatrix} =0\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-3a71f80c40e21a107c9e191948717c01_l3.png)
- Če v matriki
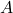 zamenjamo dve vrstici ali dva stolpca, se njena determinanta pomnoži z
zamenjamo dve vrstici ali dva stolpca, se njena determinanta pomnoži z 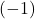 .
.
Na primer,![Rendered by QuickLaTeX.com \[\begin{vmatrix} 1& 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{vmatrix} = (-1)\cdot \begin{vmatrix} 1& 3 & 2 \\ 4 & 6 & 5 \\ 7 & 9 & 8 \end{vmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-f296f7f2da6ea925fd9b0ef713479dca_l3.png)
- Če v matriki eno vrstico ali en stolpec pomnožimo s skalarjem
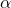 , se determinanta pomnoži z
, se determinanta pomnoži z 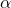 .
.
Na primer,![Rendered by QuickLaTeX.com \[\begin{vmatrix} -2 & 0 & 1\\ 4 & -3 & 2\\ 3\cdot (-1) & 3\cdot2 & 3\cdot1 \end{vmatrix} = 3\cdot \begin{vmatrix} -2 & 0 & 1\\ 4 & -3 & 2\\ -1 & 2 & 1 \end{vmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-2de97dd9f66bb70692587db71d5c97fa_l3.png)
- Če matriko pomnožimo s skalarjem
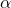 , velja
, velja 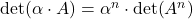 .
. - Če v matriki
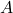 prištejemo skalarni večkratnik ene vrstice drugi vrstici, se determinanta ne spremeni. Enako velja za stolpce. To pravilo lahko uporabimo za računanje determinant. Za krajše in lažje izračune je smiselno narediti več ničel v isti vrstici ali stolpcu. To lastnost bomo uporabili v naslednjem primeru.
prištejemo skalarni večkratnik ene vrstice drugi vrstici, se determinanta ne spremeni. Enako velja za stolpce. To pravilo lahko uporabimo za računanje determinant. Za krajše in lažje izračune je smiselno narediti več ničel v isti vrstici ali stolpcu. To lastnost bomo uporabili v naslednjem primeru.
Izračunajmo determinanto matrike 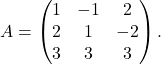
Če prvo vrstico prištejemo drugi (in prepišemo prvo in tretjo vrstico), dobimo
![Rendered by QuickLaTeX.com \[\begin{vmatrix} 1 & -1 & 2\\ 2 & 1 & -2\\ 3 & 3 & 3 \end{vmatrix} = \begin{vmatrix} 1 & -1 & 2\\ 3 & 0 & 0\\ 3 & 3 & 3 \end{vmatrix} = 3\cdot (-1)^{2+1}\cdot\begin{vmatrix} -1 & 2\\ 3 & 3 \end{vmatrix} = -3\cdot (-3-6)=27.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5fc708116d205351e21419b3033cab87_l3.png)
7. Če sta v matriki ![]() dve vrstici (ali dva stolpca) enaki, je determinanta enaka
dve vrstici (ali dva stolpca) enaki, je determinanta enaka ![]() .
.
Na primer,
![Rendered by QuickLaTeX.com \[\begin{vmatrix} 5 & 1 & 3 & -2\\ 0 & -1 & 2 & 6\\ 5 & 1 & 3 & -2\\ 0 & 4& 0 & 1 \end{vmatrix} = 0.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-e60141a79febe450546a6354591d9e17_l3.png)
8. Binetova formula: ![]() .
.
Na splošno velja ![]() , za poljubno naravno število
, za poljubno naravno število ![]() .
.
Primer 3.6: Naj bo dana matrika
![Rendered by QuickLaTeX.com \[A=\begin{pmatrix} 1 & -1 & 2\\ 2 & 1 & -2\\ 1 & 3 & 2 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-ec9d4cc7536773dcda4ddc7936dbffbd_l3.png)
Izračunajmo vrednost determinante matrike ![]() .
.
Z uporabo Binetove formule lahko pišemo
![]()
![]()
in zato je dovolj izračunati samo determinanto matrike ![]() . Ker je
. Ker je ![]() , vemo, da je
, vemo, da je ![]() .
.
Primer 3.7: Naj bo ![]() obrnljiva matrika. Koliko je vrednost determinante inverzne matrike glede na determinanto matrike
obrnljiva matrika. Koliko je vrednost determinante inverzne matrike glede na determinanto matrike ![]() ?
?
Ker je ![]() obrnljiva matrika, velja
obrnljiva matrika, velja ![]() in torej
in torej ![]() . Ker je determinanta identične matrike enaka
. Ker je determinanta identične matrike enaka ![]() , z uporabo Binetove formule to postane
, z uporabo Binetove formule to postane ![]() oziroma
oziroma
![]()
Primer 3.8: Dokažimo, da je determinanta poševno simetrične matrike lihega reda enaka nič.
Naj bo ![]() poševno simetrična matrika lihega reda
poševno simetrična matrika lihega reda ![]() . To pomeni, da je
. To pomeni, da je ![]() Ker je
Ker je ![]() liho število, dobimo
liho število, dobimo ![]() . Ampak na splošno velja
. Ampak na splošno velja ![]() , kar pomeni
, kar pomeni ![]() oziroma
oziroma ![]() .
.