6 Lastne vrednosti in lastni vektorji
Ta dva koncepta veljata samo za kvadratne matrike.
Definicija 6.1: Naj bo dana kvadratna matrika ![]() . Realno število
. Realno število ![]() imenujemo lastna vrednost za
imenujemo lastna vrednost za ![]() , če obstaja tak neničelni vektor
, če obstaja tak neničelni vektor ![]() , da je
, da je
![]()
Vektor ![]() imenujemo lastni vektor matrike
imenujemo lastni vektor matrike ![]() pri lastni vrednosti
pri lastni vrednosti ![]() .
.
Enačbo ![]() lahko zapišemo v obliki
lahko zapišemo v obliki ![]() , kjer je desna stran ničelni vektor
, kjer je desna stran ničelni vektor ![]() v
v ![]() in
in ![]() . To je homogeni sistem z neničelno rešitvijo, kar pomeni, da je
. To je homogeni sistem z neničelno rešitvijo, kar pomeni, da je ![]() . Polinom
. Polinom ![]() imenujemo karakteristični polinom matrike
imenujemo karakteristični polinom matrike ![]() (v spremenljivki
(v spremenljivki ![]() ).
).
Izrek 6.1 [4,6]: Realno število ![]() je lastna vrednost matrike
je lastna vrednost matrike ![]() natanko tedaj, ko je
natanko tedaj, ko je ![]() ničla karakterističnega polinoma
ničla karakterističnega polinoma ![]() .
.
Primer 6.1: Poiščimo lastne vrednosti in lastne vektorje matrike
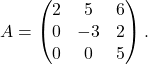
Ta matrika ima zgornjetrikotno obliko in njen karakteristični polinom je
![Rendered by QuickLaTeX.com \[p_A(\lambda)=\det(A - \lambda \cdot I_3) = \det \left[ \begin{pmatrix} 2 & 5 & 6 \\ 0 & -3 & 2 \\ 0 & 0 & 5 \end{pmatrix} - \begin{pmatrix} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda \end{pmatrix}\right] =\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-3510007c996ff0103558cf459a9501d1_l3.png)
![Rendered by QuickLaTeX.com \[\begin{vmatrix} 2-\lambda & 5 & 6 \\ 0 & -3-\lambda & 2 \\ 0 & 0 & 5-\lambda \end{vmatrix},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-e134c800e26c057add644d659e7c299e_l3.png)
ki je produkt elementov na diagonali, torej je
![]()
Ničle tega polinoma so ![]() in te so tudi lastne vrednosti matrike
in te so tudi lastne vrednosti matrike ![]() .
.
Za prvo lastno vrednost ![]() izračunamo pripadajoči lastni vektor
izračunamo pripadajoči lastni vektor ![]() , ki zadošča enačbi
, ki zadošča enačbi ![]() . Ker je
. Ker je ![]() , lahko zapišemo
, lahko zapišemo  in dobimo matrično enačbo
in dobimo matrično enačbo
![Rendered by QuickLaTeX.com \[\begin{pmatrix} 0 & 5 & 6 \\ 0 & -5 & 2 \\ 0 & 0 & 3 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5669c6186886f8a79f84806caf49a038_l3.png)
Iz tega dobimo homogeni sistem
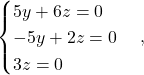
ki ima rešitev ![]() in
in ![]() je poljubno realno število. Tako sklepamo, da je
je poljubno realno število. Tako sklepamo, da je 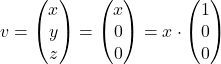 . Izberemo lahko npr. vektor
. Izberemo lahko npr. vektor 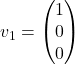 . Upoštevajte, da to pri
. Upoštevajte, da to pri ![]() ni edinstven lastni vektor, pač pa obstaja družina takšnih vektorjev, ki so vsi večkratniki vektorja
ni edinstven lastni vektor, pač pa obstaja družina takšnih vektorjev, ki so vsi večkratniki vektorja ![]() .
.
Zdaj ponovimo postopek za lastno vrednost ![]() . V matriki
. V matriki ![]() nadomestimo
nadomestimo ![]() z vrednostjo
z vrednostjo ![]() in jo potem pomnožimo s stolpcem
in jo potem pomnožimo s stolpcem ![]() Tako dobimo matrično enačbo
Tako dobimo matrično enačbo
![Rendered by QuickLaTeX.com \[\begin{pmatrix} 5 & 5 & 6 \\ 0 & 0 & 2 \\ 0 & 0 & 8 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-dc45ca2670a735a6f8ba18ca1c510b16_l3.png)
ki je ekvivalentna homogenemu sistemu
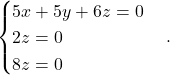
Sledi, da je ![]() in
in ![]() (ali
(ali ![]() ). Torej je
). Torej je 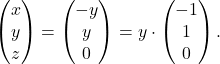 Zato lahko izberemo lastni vektor pri
Zato lahko izberemo lastni vektor pri ![]() , npr. vektor
, npr. vektor 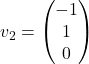 .
.
Na koncu poiščemo še lastni vektor pri ![]() . V matriki
. V matriki ![]() nadomestimo
nadomestimo ![]() s
s ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{pmatrix} -3 & 5 & 6 \\ 0 & -8 & 2 \\ 0 & 0 & 0 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-e8086a74fa6482984cad45cab7b1cacd_l3.png)
Pripadajoči homogeni sistem je
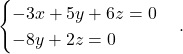
Ker je ![]() , sledi, da je pripadajoči sistem rešljiv in je rešitev odvisna od enega parametra. Iz enačbe
, sledi, da je pripadajoči sistem rešljiv in je rešitev odvisna od enega parametra. Iz enačbe ![]() dobimo
dobimo ![]() , z
, z ![]() Potem izračunamo
Potem izračunamo ![]() in
in 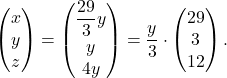 Zato izberemo lastni vektor pri
Zato izberemo lastni vektor pri ![]() , npr. vektor
, npr. vektor 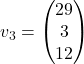 .
.
Opomba. Za izračun lastnih vrednosti dane matrike ne moremo uporabiti Gaussove eliminacijske metode. Če to metodo uporabimo za pretvorbo matrike ![]() v zgornje trikotno matriko
v zgornje trikotno matriko ![]() , so lastne vrednosti matrike
, so lastne vrednosti matrike ![]() lahko drugačne od lastnih vrednosti matrike
lahko drugačne od lastnih vrednosti matrike ![]() .
.
Definicija 6.2: Naj bo ![]() lastna vrednost za matriko
lastna vrednost za matriko ![]() . Večkratnost
. Večkratnost ![]() kot ničle karakterističnega polinoma
kot ničle karakterističnega polinoma ![]() imenujemo algebraična večkratnost lastne vrednosti
imenujemo algebraična večkratnost lastne vrednosti ![]() . Označimo jo z
. Označimo jo z ![]() (tj. stopnja ničle
(tj. stopnja ničle ![]() v polinomu
v polinomu ![]() ).
).
Poleg tega ![]() imenujemo geometrična večkratnost lastne vrednosti
imenujemo geometrična večkratnost lastne vrednosti ![]() , označimo jo z
, označimo jo z ![]() .
.
Na primer, če je karakteristični polinom ![]() , potem imamo
, potem imamo ![]() ,
, ![]() in
in ![]() .
.
Izrek 6.2 [4,6]:
Naj bo ![]() poljubna kvadratna matrika reda
poljubna kvadratna matrika reda ![]() .
.
- Vsota vseh algebraičnih večkratnosti lastnih vrednosti matrike
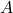 je enaka
je enaka  .
. - Vsota vseh lastnih vrednosti matrike
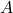 , štetih z njihovo večkratnostjo, je enaka vsoti vseh diagonalnih elementov matrike
, štetih z njihovo večkratnostjo, je enaka vsoti vseh diagonalnih elementov matrike 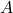 . Imenujemo jo sled matrike in jo označimo
. Imenujemo jo sled matrike in jo označimo 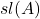 .
. - Vedno velja
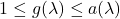 .
.
Primer 6.2: Poiščimo lastne vrednosti in lastne vektorje matrike
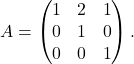
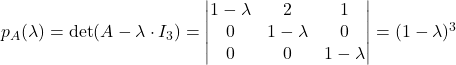 . Zato je
. Zato je  je
je Pripadajoči homogeni sistem vsebuje samo eno enačbo, in to je
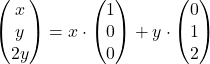 , kar pomeni, da lahko izberemo lastna vektorja
, kar pomeni, da lahko izberemo lastna vektorja 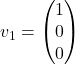 in
in 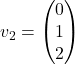 .
.Primer 6.3: Poiščimo lastne vrednosti in lastne vektorje matrike
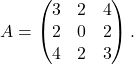
Začnemo s karakterističnim polinomom matrike ![]() , ki je
, ki je
![Rendered by QuickLaTeX.com \[p_A(\lambda)=\begin{vmatrix} 3-\lambda & 2 & 4 \\ 2 & -\lambda & 2\\ 4 & 2 & 3-\lambda \end{vmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-01e09f934f452ff0f43e6e897946c1fa_l3.png)
Z razvojem po drugi vrstici dobimo
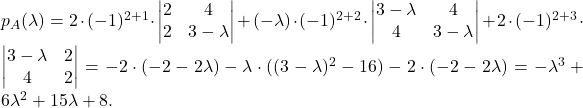
Z uporabo Hornerjevega algoritma izračunamo ničle tega polinoma:
![Rendered by QuickLaTeX.com \[\begin{array}{rrrrrrrrr} &\vline&-1&&6&&15&&8\\ &\vline&&&1&&-7&&-8\\ \hline&\vline&&&&&&&\\ -1&\vline&-1&&7&&8&&0 \end{array}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-58a0df02d3cb12a9863f230f840ecd66_l3.png)
Ponovimo algoritem in dobimo
![Rendered by QuickLaTeX.com \[\begin{array}{rrrrrrr} &\vline&-1&&7&&8\\ &\vline&&&1&&-8\\ \hline&\vline&&&&&\\ -1&\vline&-1&&8&&0 \end{array}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-6e6e7e9442763963b1960ff7c703e309_l3.png)
Zdaj lahko zapišemo ![]() . Torej, lastni vrednosti dane matrike sta:
. Torej, lastni vrednosti dane matrike sta: ![]() z
z ![]() in
in ![]() z
z ![]() .
.
Izračunamo rang matrike ![]() pri vrednostih
pri vrednostih ![]() in
in ![]() . Da bi to naredili, matriko
. Da bi to naredili, matriko ![]() preoblikujemo v vrstično kanonično obliko.
preoblikujemo v vrstično kanonično obliko.
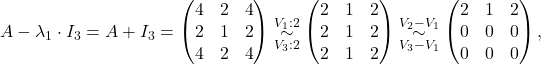
torej je ![]() in geometrična večkratnost lastne vrednosti
in geometrična večkratnost lastne vrednosti ![]() je
je ![]() Pripadajoči lastni vektor
Pripadajoči lastni vektor 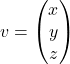 zadošča enačbi
zadošča enačbi
![Rendered by QuickLaTeX.com \[\begin{pmatrix} 2 & 1 & 2 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-1e321d12adc2dce18b1a54f5da250ec4_l3.png)
ki je ekvivalentna enačbi ![]() , iz katere sledi, da je
, iz katere sledi, da je ![]() . Torej, lastni vektorji pri
. Torej, lastni vektorji pri ![]() so oblike
so oblike 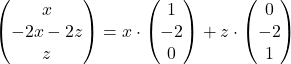 in lahko izberemo npr.
in lahko izberemo npr. 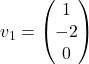 in
in 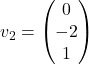 .
.
Enak postopek ponovimo za lastno vrednost ![]() .
.
![Rendered by QuickLaTeX.com \[A-\lambda_2\cdot I_3=A-8\cdot I_3= \begin{pmatrix} -5 & 2 & 4 \\ 2 & -8 & 2 \\ 4 & 2 & -5 \end{pmatrix}\overset{V_2:2}{\sim} \begin{pmatrix} -5 & 2 & 4 \\ 1 & -4 & 1 \\ 4 & 2 & -5 \end{pmatrix}\overset{V_1\leftrightarrow V_2}{\sim}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5a2622e63e5d6e9aee4944c40c0a265e_l3.png)
![Rendered by QuickLaTeX.com \[\begin{pmatrix} 1 & -4 & 1 \\ -5 & 2 & 4 \\ 4 & 2 & -5 \end{pmatrix}\overset{V_2+5V_1}{\underset{V_3-4V_1}{\sim}} \begin{pmatrix} 1 & -4 & 1 \\ 0 & -18 & 9 \\ 0 & 18 & -9 \end{pmatrix}\overset{V_3+ V_2}{\sim} \begin{pmatrix} 1 & -4 & 1 \\ 0 & -18 & 9 \\ 0 & 0 & 0 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-8136c878169c8704b3c2ebe8a30c9dda_l3.png)
Sledi, da je ![]() , in zato geometrična večkratnost lastne vrednosti
, in zato geometrična večkratnost lastne vrednosti ![]() je
je ![]() Lastni vektor pri
Lastni vektor pri ![]() zadošča enačbi
zadošča enačbi
![Rendered by QuickLaTeX.com \[\begin{pmatrix} 1 & -4 & 1 \\ 0 & -18 & 9 \\ 0 & 0 & 0 \end{pmatrix}\cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-a631858882bac0fd61a2821f7dff9f4f_l3.png)
oziroma zadošča sistemu
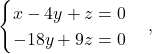
ki ima rešitev ![]() ,
, ![]() , kjer je
, kjer je ![]() poljubno realno število. Torej ima lastni vektor pri
poljubno realno število. Torej ima lastni vektor pri ![]() splošno obliko
splošno obliko 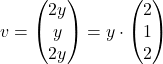 in izberemo npr.
in izberemo npr. 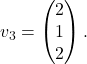
Lastnosti [4,6]:
- lastne vrednosti trikotne matrike so enake diagonalnim elementom;
- determinanta matrike je enaka produktu lastnih vrednosti;
- če ima matrika
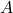 lastno vrednost
lastno vrednost 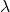 in lastni vektor
in lastni vektor  , potem
, potem
ima inverzna matrika lastno vrednost in isti lastni vektor
in isti lastni vektor  ;
; - če ima matrika
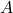 lastno vrednost
lastno vrednost 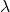 in lastni vektor
in lastni vektor  , potem
, potem
ima matrika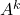 lastno vrednost
lastno vrednost 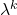 in isti lastni vektor
in isti lastni vektor  .
.