10 Limita funkcije
Definicija 10.1: Naj bo ![]() notranja točka intervala
notranja točka intervala ![]() in
in ![]() dana funkcija. Število
dana funkcija. Število ![]() je limita funkcije
je limita funkcije ![]() v točki
v točki ![]() , če za vsak
, če za vsak ![]() obstaja tak
obstaja tak ![]() , da za vsak
, da za vsak ![]() velja:
velja:
![]()
To pomeni: vrednost ![]() je poljubno blizu
je poljubno blizu ![]() , ko je
, ko je ![]() dovolj blizu
dovolj blizu ![]() (ampak
(ampak ![]() ). Pišemo
). Pišemo ![]() (in beremo
(in beremo ![]() je limita funkcije
je limita funkcije ![]() , ko gre
, ko gre ![]() proti
proti ![]() ).
).
Za naslednje limite lahko uporabimo metodo vstavljanja.
Primer 10.1: Izračunajmo limite:
Če je točka ![]() ničla števca in imenovalca dane racionalne funkcije, najprej razstavimo števec in imenovalec, potem pa pokrajšamo skupni faktor.
ničla števca in imenovalca dane racionalne funkcije, najprej razstavimo števec in imenovalec, potem pa pokrajšamo skupni faktor.
Primer 10.2: Izračunajmo limite:
-
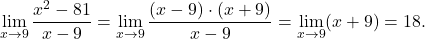
-
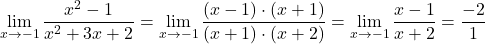 .
. -
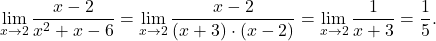
Operacije z limitami
Izrek 10.1 [5,9]: Naj bo ![]() in
in ![]() . Potem velja:
. Potem velja:
-
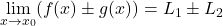 ;
; -
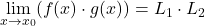 ;
; -
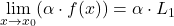 , za poljubno
, za poljubno 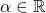 ;
; -
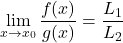 , če je
, če je 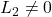 ;
; -
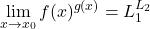 , če je
, če je 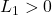 .
.
Enostranske limite
Definicija 10.2: Pravimo, da je realno število ![]()
(i) leva limita funkcije ![]() v točki
v točki ![]() , če za vsak
, če za vsak ![]() obstaja tak
obstaja tak ![]() , da je
, da je ![]() , če je
, če je ![]()
(to pomeni, da se ![]() številu
številu ![]() približuje z leve strani); pišemo
približuje z leve strani); pišemo
![]()
(ii) desna limita funkcije ![]() v točki
v točki ![]() , če za vsak
, če za vsak ![]() obstaja tak
obstaja tak ![]() , da je
, da je ![]() , če je
, če je ![]()
(to pomeni, da se ![]() številu
številu ![]() približuje z desne strani); pišemo
približuje z desne strani); pišemo
![]()
Izrek 10.2 [5,9]: Funkcija ![]() ima v točki
ima v točki ![]() limito natanko tedaj, ko ima v točki
limito natanko tedaj, ko ima v točki ![]() tako levo kot desno limito in sta ti dve limiti enaki.
tako levo kot desno limito in sta ti dve limiti enaki.
Primer 10.3: Izračunajmo levo in desno limito v točki ![]() funkcije, podane s predpisom
funkcije, podane s predpisom
![Rendered by QuickLaTeX.com \[f(x) = \begin{cases} x^2,&\textup{če je }x \geq 2,\\ x-3,&\textup{če je }x < 2. \end{cases}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-087ae1d2c7951c394098e6588961424a_l3.png)
Velja ![]() in
in ![]() Torej ugotovimo, da ne obstaja limita
Torej ugotovimo, da ne obstaja limita ![]() .
.
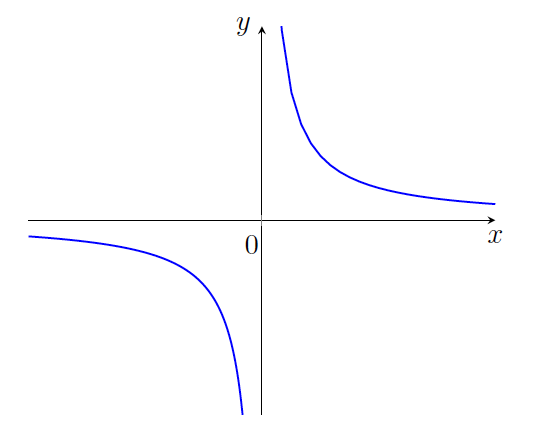
Primer 10.4: Dana je funkcija s predpisom ![]() Domena te funkcije je
Domena te funkcije je ![]() in njen graf je na sliki 10.1.
in njen graf je na sliki 10.1.
 .
.Z grafa funkcije razberemo, da ko gre ![]() proti
proti ![]() , se vrednost funkcije
, se vrednost funkcije ![]() približuje
približuje ![]() , torej je
, torej je
![]()
in ko gre ![]() proti
proti ![]() , se vrednost funkcije
, se vrednost funkcije ![]() približuje
približuje ![]() , torej je
, torej je
![]()
Poleg tega v točki ![]() funkcija ni definirana in veljata:
funkcija ni definirana in veljata:
![]()
![]()
To pomeni, da limita ![]() ne obstaja.
ne obstaja.
Primer 10.5: Naj bo funkcija ![]() podana s predpisom
podana s predpisom ![]() Ugotovimo, ali obstaja
Ugotovimo, ali obstaja ![]() .
.
Na podlagi definicije absolutne vrednosti zapišemo
![Rendered by QuickLaTeX.com \[f(x)=\begin{cases} x,&\textup{če je }x \geq 0,\\ -x,&\textup{ če je }x < 0,\end{cases}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-11499560d5651d0daff8cd26c7cb23bd_l3.png)
in torej dobimo
![]()
ter
![]()
kar pomeni, da je ![]()
Primer 10.6: Naj bo funkcija ![]() podana s predpisom
podana s predpisom ![]() . Ugotovimo, ali obstaja
. Ugotovimo, ali obstaja ![]() .
.
Ker je
![Rendered by QuickLaTeX.com \[\lvert x-1\rvert=\begin{cases} x-1, &\textup{če je }x-1 \geq 0,\\ -(x-1), &\textup{če je }x-1<0,\end{cases}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5087a571b2fcc34f2fe5025ec2b393b0_l3.png)
lahko izračunamo
![]()
in podobno
![]()
Torej limita ![]() ne obstaja.
ne obstaja.
Limita v neskončnosti
Pravimo, da je
1. ![]() , če za vsak
, če za vsak ![]() obstaja tak
obstaja tak ![]() , da je
, da je ![]() za vsak
za vsak ![]()
2. ![]() , če za vsak
, če za vsak ![]() obstaja tak
obstaja tak ![]() , da je
, da je ![]() za vsak
za vsak ![]()
Primer 10.7: Izračunajmo naslednje limite:
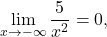 ker je
ker je 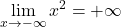 .
.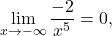 ker je
ker je 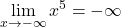 .
.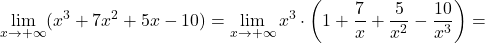
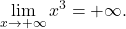
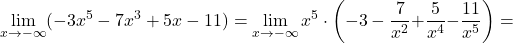
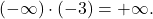
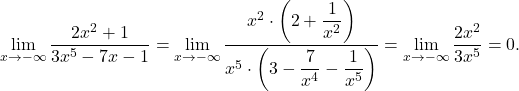
Neskončna limita
Dana je funkcija ![]() . Pravimo, da je
. Pravimo, da je
1. ![]() , če za vsak
, če za vsak ![]() obstaja tak
obstaja tak ![]() , da je
, da je ![]() za vsak
za vsak ![]() tako, da je
tako, da je ![]()
2. ![]() , če za vsak
, če za vsak ![]() obstaja tak
obstaja tak ![]() , da je
, da je ![]() za vsak
za vsak ![]() tako, da je
tako, da je ![]()
Primer 10.8: Izračunajmo naslednje limite:
Primer 10.9: Ali je ![]() ?
?
Najprej napišemo izraz absolutne vrednosti
![Rendered by QuickLaTeX.com \[\lvert x-3 \rvert = \begin{cases} x-3, &\textup{če je }x-3 \geq 0 \Leftrightarrow x\geq 3,\\ -(x-3),&\textup{če je }x-3 < 0 \Leftrightarrow x<3. \end{cases}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-140ce80cf6978e4d04b4ad3feeb4c020_l3.png)
Če je ![]() , izračunamo desno limito dane funkcije:
, izračunamo desno limito dane funkcije:
![]()
in če je ![]() , izračunamo levo limito:
, izračunamo levo limito:
![]()
Ker sta leva in desna limita enaki, je ![]() .
.
Primer 10.10: Izračunajmo limito ![]()
Začnemo z izrazom absolutne vrednosti
![Rendered by QuickLaTeX.com \[\lvert x-1 \rvert = \begin{cases} x-1, &\textup{če je }x-1 \geq 0 \Leftrightarrow x\geq 1,\\ -(x-1),&\textup{če je }x-1 < 0 \Leftrightarrow x<1. \end{cases}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-1325e69980ea3d6090e8e29f5f83759a_l3.png)
Zdaj izračunamo desno in potem levo limito v točki ![]() :
:
![]()
![]()
![]()
Ker dve limiti nista enaki, sklepamo, da limita ![]() ne obstaja.
ne obstaja.
Limita elementarnih funkcij
Polinomska funkcija
Izraz oblike
![]()
imenujemo polinom spremenljvke ![]() . Če je
. Če je ![]() , je stopnja polinoma
, je stopnja polinoma ![]() enaka
enaka ![]() in koeficientu
in koeficientu ![]() pri najvišji potenci
pri najvišji potenci ![]() pravimo vodilni koeficient. Domena polinomske funkcije je
pravimo vodilni koeficient. Domena polinomske funkcije je ![]() . Velja:
. Velja:
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} P(x)= a_n \cdot (+\infty) = \begin{cases} +\infty, &\textup{\v ce je }a_n >0,\\ -\infty, &\textup{\v ce je }a_n < 0, \end{cases}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-9d4fae14698f2a0d9aee862ee5397356_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} P(x)= \begin{cases} a_n \cdot (+\infty) ,&\textup{\v ce je }n \textup{ sodo \v stevilo,} \\ a_n \cdot (-\infty), & \textup{\v ce je }n\textup{ liho \v stevilo.} \end{cases}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-e6281f1fbad56304efe573e4c23348d0_l3.png)
![]()
Primer 10.11: Izračunajmo limito
![]()
Racionalna funkcija
Racionalna funkcija, tj. kvocient dveh polinomov, ima splošno obliko
![]()
Ničle racionalne funkcije ![]() so ničle polinoma
so ničle polinoma ![]() , če polinoma
, če polinoma ![]() in
in ![]() nimata skupnih ničel, poli pa so ničle polinoma
nimata skupnih ničel, poli pa so ničle polinoma ![]() . Domena funkcije
. Domena funkcije ![]() je torej
je torej ![]() .
.
Limito v neskončnosti izračunamo po metodi, da v števcu in imenovalcu izpostavimo ![]() na najvišji potenci:
na najvišji potenci:
![]()
![Rendered by QuickLaTeX.com \[&=\lim_{x \to \pm \infty} \frac{x^n\cdot (a_n + \dfrac{a_{n-1}}{x}+\cdots + \dfrac{a_0}{x^n})}{x^m\cdot (b_m+ \dfrac{b_{m-1}}{x}+\cdots + \dfrac{b_0}{x^m})}=\begin{cases} \dfrac{a_n}{b_m}, &\text{\v ce je }m= n, \\ \pm\infty, & \text{\v ce je }m < n,\\0,&\text{\v ce je } m > n. \end{cases}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-79f2277af866d7c4c3a0a4fd065af6a2_l3.png)
Primer 10.12: Izračunajmo naslednje limite:
-
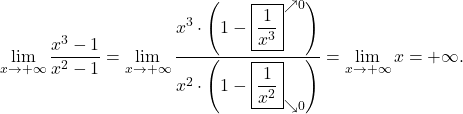
-
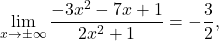 ker sta stopnji števca in imenovalca enaki.
ker sta stopnji števca in imenovalca enaki. -
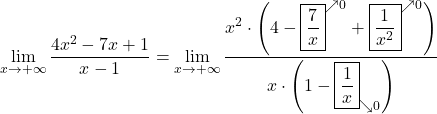
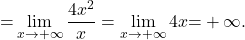
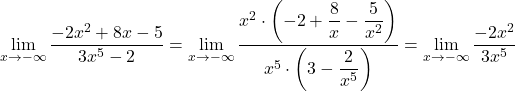
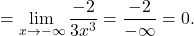
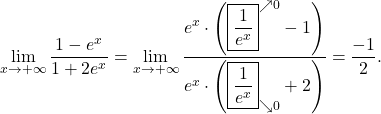
Ko izračunamo limito racionalne funkcije v polu, razstavimo imenovalec, in če je pol ničla tudi za števec, potem razstavimo števec ter pokrajšamo skupni faktor.
Primer 10.13: Izračunajmo naslednje limite:
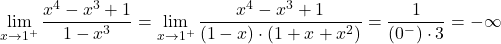 .
.-
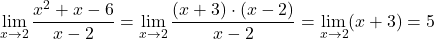 .
. 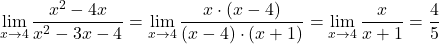 .
.
Iracionalna funkcija
Pri računanju limit iracionalnih funkcij, tj. funkcij, v katerih nastopajo koreni, uporabimo metodo razširjanja.
Primer 10.14: Izračunajmo naslednje limite:
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to 0} \frac{\sqrt{1+x}-1}{x} \stackrel{\left[\frac{0}{0}\right]}= \lim_{x \to 0} \frac{\sqrt{1+x}-1}{x} \cdot\frac{\sqrt{1+x}+1}{\sqrt{1+x}+1}=\lim_{x \to 0} \frac{(\sqrt{1+x})^2-1^2}{x\cdot (\sqrt{1+x}+1)}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-06abce8841b686cdb507e4960df4ddf1_l3.png)
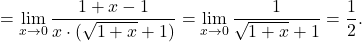
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to 1}\frac{2 - \sqrt{x+3}}{\sqrt{2x-1}-1}\stackrel{\left[\frac{0}{0}\right]}{=}\lim_{x \to 1} \frac{2 - \sqrt{x+3}}{\sqrt{2x-1}-1}\cdot\frac{2 + \sqrt{x+3}}{2 + \sqrt{x+3}}\cdot\frac{\sqrt{2x-1}+1}{\sqrt{2x-1}+1} &=](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-42074711bc0eaa5fdae5a9f0468dec6a_l3.png)
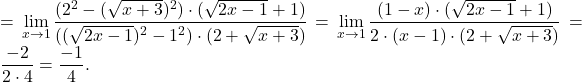
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to -\infty} (\sqrt{x^2+4}+x) \stackrel{\left[ \infty-\infty\right]}{=}\lim_{x \to -\infty} (\sqrt{x^2+4}+x) \cdot \frac{\sqrt{x^2+4}-x}{\sqrt{x^2+4}-x}=](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-38105bf8c7b5e1274400c8ff54d6d835_l3.png)
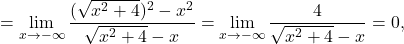 kjer je
kjer je 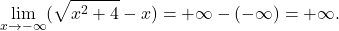
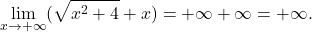
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to -\infty} (\sqrt{x^2+x} - \sqrt{x^2 - x}) \stackrel{\left[ \infty-\infty\right]}{=}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-449bd63c2c6a3c83ce1d0ea9691f9efb_l3.png)
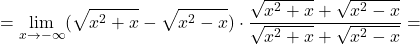
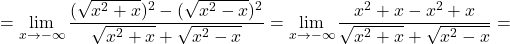

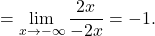
![Rendered by QuickLaTeX.com \displaystyle\lim_{x \to -\infty}\frac{\sqrt{2x^2+2}-x}{x} \stackrel{\left[\frac{+\infty}{-\infty}\right]}{=}\lim_{x \to -\infty}\frac{\sqrt{2x^2+2}-x}{x}\cdot \frac{\sqrt{2x^2+2}+x}{\sqrt{2x^2+2}+x}=](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-eff925da8d5c4f70c48b0c4355f78e38_l3.png)
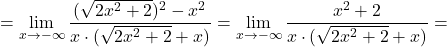
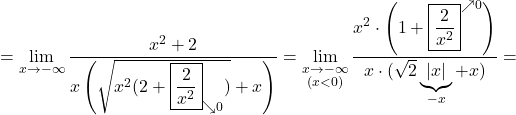
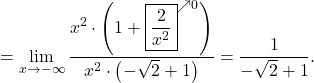
Eksponentna funkcija (nedoločena oblika ![]() )
)
Eksponentna funkcija ima splošno obliko ![]() , kjer je
, kjer je ![]() poljubno realno število, ki se imenuje osnova,
poljubno realno število, ki se imenuje osnova, ![]() pa eksponent. Domena te funkcije je
pa eksponent. Domena te funkcije je ![]() , zaloga vrednosti pa
, zaloga vrednosti pa ![]() , zato funkcija nima ničle.
, zato funkcija nima ničle.
Za ![]() je eksponentna funkcija strogo naraščajoča in velja:
je eksponentna funkcija strogo naraščajoča in velja:
![]()
Za ![]() je eksponentna funkcija strogo padajoča in velja:
je eksponentna funkcija strogo padajoča in velja:
![]()
Grafa eksponentne funkcije sta na sliki 10.2.
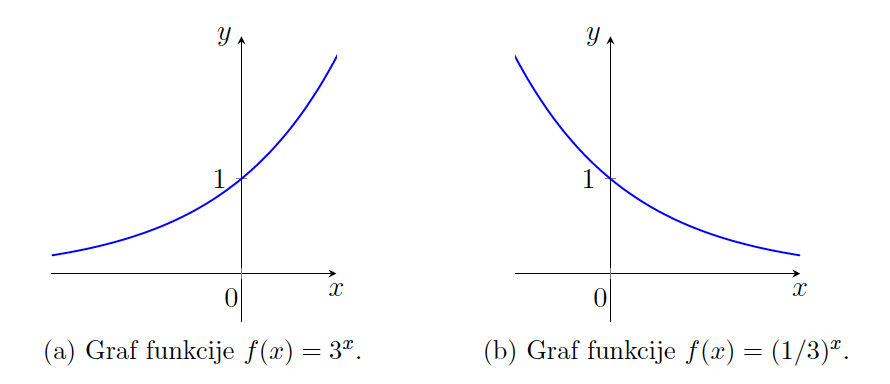
Izrek 10.3 [5,9]:
Velja ![]() . Velja tudi limita
. Velja tudi limita
![]()
kjer je ![]() .
.
Primer 10.15: Izračunajmo limito ![]() .
.
Ker sta ![]() in
in ![]() , je dana limita v nedoločeni obliki
, je dana limita v nedoločeni obliki ![]() in za njen izračun torej uporabimo formulo (1). Najprej osnovo
in za njen izračun torej uporabimo formulo (1). Najprej osnovo ![]() napišemo v obliki
napišemo v obliki ![]() in potem uredimo eksponent, da dano funkcijo zapišemo v obliki
in potem uredimo eksponent, da dano funkcijo zapišemo v obliki
![Rendered by QuickLaTeX.com \[\left[\left(1+\dfrac{1}{f(x)}\right)^{f(x)}\right]^{\frac{1}{f(x)}\cdot g(x)},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4de54937ec2f011a579379fcc61b41c9_l3.png)
kjer je ![]() začetni eksponent. Potem je
začetni eksponent. Potem je
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} \left[\left(1+\dfrac{1}{f(x)}\right)^{f(x)}\right]^{\frac{1}{f(x)}\cdot g(x)}=e^{\displaystyle\lim_{x \to +\infty}\frac{g(x)}{f(x)}}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-c30c12cd09e507315b3b1e04e51ee1ce_l3.png)
V našem primeru je ta postopek sledeč:
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com =\displaystyle\lim_{x \to +\infty} \left[\underbrace{\left(1+\frac{1}{-(x+1)}\right)^{-(x+1)}}_{e}\right]^{\frac{1}{-(x+1)}\cdot (x+1)}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-243ed33802f6952526cc076bfb304d43_l3.png)
![]()
![]()
Primer 10.16: Izračunajmo limito ![]() .
.
Dana limita je v nedoločeni obliki ![]() , torej tukaj lahko uporabimo formulo (1):
, torej tukaj lahko uporabimo formulo (1):
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle=\lim_{x \to +\infty}\left[\left(1+\frac{1}{\frac{x-2}{5}}\right)^{\frac{x-2}{5}}\right]^{\frac{5}{x-2}\cdot x}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-daeac4fedefc652fb339e0e68d850040_l3.png)
![]()
![]()
Primer 10.17: Izračunajmo limito ![]() .
.
Ta limita je podana v nedoločeni obliki ![]() , torej uporabimo formulo (1).
, torej uporabimo formulo (1).
![Rendered by QuickLaTeX.com \[\lim_{x \to 0} (1+x)^{\frac{1}{x}} =\lim_{x \to 0}\left[ \left(1+\frac{1}{\frac{1}{x}}\right)^{\frac{1}{x}} \right]^{x\cdot\frac{1}{x}}= e^{\displaystyle\lim_{x \to 0}(x\cdot \dfrac{1}{x})}=e.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5a35302e59af59de60c1392f417ffeb5_l3.png)
Primer 10.18: Izračunajmo limito ![]() .
.
Najprej izračunamo limito
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} \dfrac{x+\sqrt{x}}{x-\sqrt{x}}=\lim_{x \to +\infty} \dfrac{x \cdot\left(1+\dfrac{\sqrt{x}}{x}\right)}{x\cdot\left( 1-\dfrac{\sqrt{x}}{x}\right)}=\lim_{x \to +\infty} \dfrac{1+\boxed{\frac{1}{\sqrt{x}}}^{\nearrow 0}}{1-\boxed{\frac{1}{\sqrt{x}}}_{\searrow 0}}=1,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-6fe1e483d200606bf43caeb5455d5349_l3.png)
torej je dana limita v nedoločeni obliki ![]() . Zato izračunamo
. Zato izračunamo
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com =\displaystyle\lim_{x \to +\infty} \left[\left(1+\dfrac{1}{\frac{x-\sqrt{x}}{2\sqrt{x}}}\right)^{\frac{x-\sqrt{x}}{2\sqrt{x}}}\right]^{\frac{2\sqrt{x}}{x-\sqrt{x}}\cdot \sqrt{x}}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-a47af1539959fe64874ea644c03856b5_l3.png)
![]()
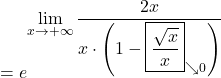
![]()
Logaritemska funkcija
Inverzna funkcija eksponentne funkcije je logaritemska funkcija, definirana, kot sledi:
![]()
Domena logaritemske funkcije ![]() z osnovo
z osnovo ![]() , in
, in ![]() . Ker je
. Ker je ![]() , dobimo, da je ničla logaritemske funkcije točka
, dobimo, da je ničla logaritemske funkcije točka ![]() , torej je
, torej je ![]() . Za
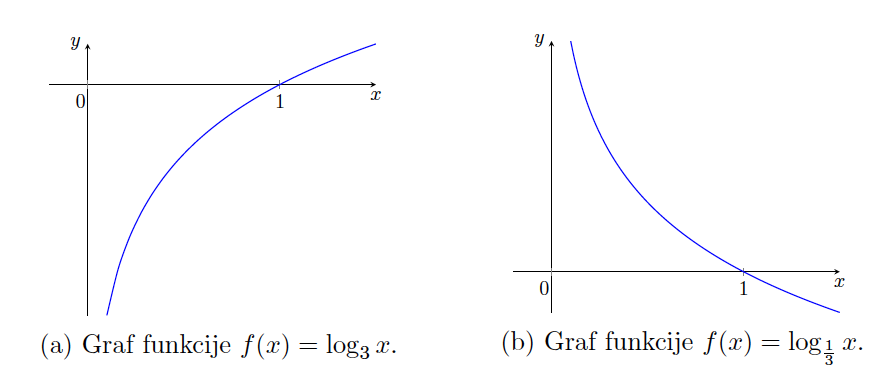
. Za ![]() je logaritemska funkcija strogo naraščajoča (njen graf je na sliko 10.3 na levi) in za
je logaritemska funkcija strogo naraščajoča (njen graf je na sliko 10.3 na levi) in za ![]() je logaritemska funkcija strogo padajoča (njen graf je na sliko 10.3 na desni). Logaritmu z osnovo
je logaritemska funkcija strogo padajoča (njen graf je na sliko 10.3 na desni). Logaritmu z osnovo ![]() pravimo naravni logaritem in ga pišemo
pravimo naravni logaritem in ga pišemo ![]() .
.
Primer 10.19: Izračunajmo limito ![]() .
.
Z uporabo formule ![]() lahko napišemo
lahko napišemo
![]()
Ker je logaritemska funkcija zvezna, lahko napišemo
![]()
na podlagi limite v primeru 10.17.
V bolj splošnem primeru imamo temeljno limito
![]()
Primer 10.20: Izračunajmo limito ![]() .
.
Uredimo dano funkcijo, da lahko uporabimo formulo (2):
![Rendered by QuickLaTeX.com \[\lim_{x \to 0} \frac{\ln {(1+3x)}}{\ln (1+7x)} = \lim_{x \to 0} \frac{\boxed{\frac{\ln(1+3x)}{3x}}^{\nearrow 1} \cdot 3x}{\boxed{\frac{\ln(1+7x)}{7x}}_{\searrow 1} \cdot 7x} =\frac{3}{7}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-d0a845b816e0e67b39404691e91a48b5_l3.png)
Primer 10.21: Izračunajmo limito ![]() .
.
![]()
![]()
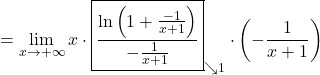
![]()
kjer smo upoštevali, da je ![]() , in smo zato uporabili formulo (2).
, in smo zato uporabili formulo (2).
Izrek 10.4 [5,9] : Velja ![]() , ker je
, ker je ![]() . Velja tudi limita
. Velja tudi limita
![]()
kjer je ![]() .
.
Primer 10.22: Izračunajmo limito ![]()
![Rendered by QuickLaTeX.com \[\lim_{x \to 0}\dfrac{2^{3x}-1}{x}=\lim_{x \to 0}\boxed{\dfrac{2^{3x}-1}{3x}}_{\searrow \ln 2}\cdot \frac{3x}{x}=3\ln 2=\ln 8.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-35f5817a929a9701b42ddf6e46aca058_l3.png)
Primer 10.23: Izračunajmo limito ![]()
![Rendered by QuickLaTeX.com \[\lim_{x \to 1}\dfrac{3x^2+x-4}{2^{3x-3}-1}=\lim_{x \to 1}\dfrac{3\cdot (x-1)\cdot (x+\frac{4}{3})}{2^{3x-3}-1}=\lim_{x \to 1}\dfrac{(3x-3)\cdot (x+\frac{4}{3})}{\boxed{\dfrac{2^{3x-3}-1}{3x-3}}_{\searrow \ln 2}\cdot (3x-3)}=\dfrac{7}{3}\cdot\frac{1}{\ln 2}=\dfrac{7}{3\ln 2}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-1cb97ce5889a499e8af89cee9d5b0f03_l3.png)
Primer 10.24: Izračunajmo limito ![]()
![Rendered by QuickLaTeX.com \[\lim_{x \to 1}\dfrac{x-1}{e^x-e}=\lim_{x \to 1}\dfrac{x-1}{e\cdot (e^{x-1}-1)}=\lim_{x \to 1}\dfrac{x-1}{e\cdot \boxed{\dfrac{e^{x-1}-1}{x-1}}_{\searrow \ln e=1}\cdot (x-1)}=\dfrac{1}{e}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-b3d82af2a2d43070a95c63ccbbd5f429_l3.png)
Trigonometrične funkcije
Najprej se spomnimo grafov štirih temeljnih funkcij (glej sliko 10.4).
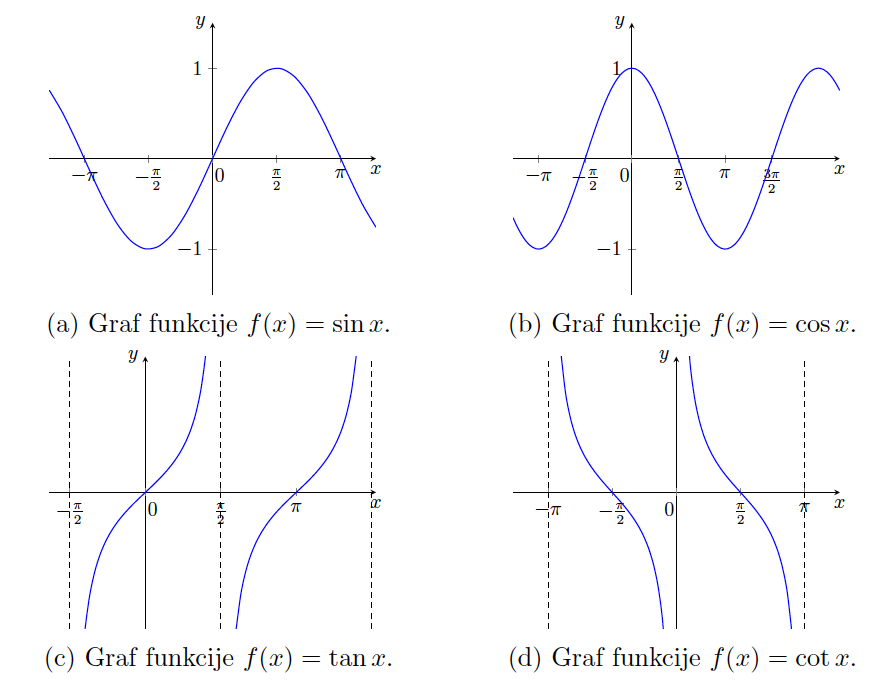
Funkciji sinus in kosinus sta periodični z osnovno periodo ![]() , tangens in kotangens pa s periodo
, tangens in kotangens pa s periodo ![]() . To pomeni, da velja
. To pomeni, da velja ![]() ter
ter ![]() , za poljubno
, za poljubno ![]() .
.
Funkcija kosinus je soda, torej je ![]() , funkcije sinus, tangens in kotangens pa so lihe:
, funkcije sinus, tangens in kotangens pa so lihe: ![]() in
in ![]() .
.
Najpomembnejše formule s trigonometričnimi funkcijami so:
-
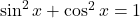 ;
; -
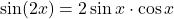 ;
; 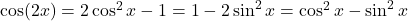 ;
;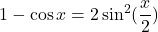 .
.
Takoj opazimo še naslednje lastnosti:
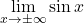 ne obstaja;
ne obstaja;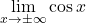 ne obstaja;
ne obstaja;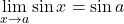 ;
;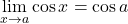 ;
;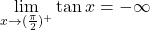 ;
;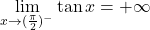 ;
;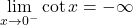 ;
;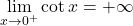 .
.
Izrek 10.5 [Izrek o sendviču] [5]: Če je ![]() in je
in je ![]() za vse
za vse ![]() blizu
blizu ![]() (razen za
(razen za ![]() ), potem obstaja tudi limita
), potem obstaja tudi limita ![]() in je enaka
in je enaka ![]() .
.
Primer 10.25: Dokažimo, da je ![]() .
.
Potem velja tudi
![]()
Ker je ![]() , če neenačbo delimo s
, če neenačbo delimo s ![]() , dobimo
, dobimo ![]() , kar zapišemo v obliki
, kar zapišemo v obliki
![]()
Zdaj, po izreku 10.5, sledi ![]() , saj je
, saj je ![]() .
.
Primer 10.26: Dokažimo, da je ![]()
Ker je funkcija sinus omejena, dobimo
![]()
in če pomnožimo z ![]() , neenačba postane
, neenačba postane
![]()
Po izreku 10.5 sledi ![]() saj je
saj je ![]() .
.
Primer 10.27: Izračunajmo limito ![]() .
.
![Rendered by QuickLaTeX.com \[\lim_{x \to 0}\frac{\tan x}{x} = \lim_{x \to 0}\frac{\sin x}{\cos x} \cdot\frac{1}{x}= \lim_{x \to 0}\boxed{\frac{\sin x}{x}}_{\searrow 1}\cdot\frac{1}{\cos x}=1\cdot\frac{1}{\cos 0}= 1.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-89563f9412943fb51f9d12a4bb1f81ca_l3.png)
Primer 10.28: Izračunajmo limito ![]() .
.
![Rendered by QuickLaTeX.com \[\displaystyle{\lim_{x \to 0}\frac{\sin (7x)}{\sin (5x)} =\lim_{x \to 0}\dfrac{\boxed{\frac{\sin (7x)}{7x}}^{\nearrow 1} \cdot 7x}{\boxed{\frac{\sin (5x)}{5x}}_{\searrow 1}\cdot 5x} =\frac{7}{5}.}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-b14cbeffe5d6506e5c8d0fe857b7321f_l3.png)
Primer 10.29: Izračunajmo limito ![]() .
.
![Rendered by QuickLaTeX.com \[\displaystyle{\lim_{x \to 0}\frac{1 - \cos x}{x^2} = \lim_{x \to 0}\frac{2\cdot\sin^2 \left(\frac{x}{2}\right)}{\frac{x}{2} \cdot \frac{x}{2}\cdot 4} = \frac{1}{2}\cdot \boxed{\dfrac{\sin \frac{x}{2}}{\frac{x}{2}}}_{\searrow 1} \cdot \boxed{\frac{\sin \frac{x}{2}}{\frac{x}{2}}}_{\searrow 1}= \frac{1}{2}.}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-6d3a7e600c74dbf658137023ed51d73f_l3.png)
Primer 10.30: Izračunajmo limito ![]() .
.
Ker je dana limita v nedoločeni obliki ![]() , uporabimo formulo (1):
, uporabimo formulo (1):
![]()
![Rendered by QuickLaTeX.com =\displaystyle\lim_{x \to 0} \left[ \left(1 + \frac{1}{\frac{1}{1-\cos x}}\right)^{\frac{1}{1- \cos x}} \right]^{\frac{1- \cos x}{x^2}}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-7675274ab40e58914a2ceebd3642f765_l3.png)
![]()
![]()
![]()
Primer 10.31: Izračunajmo limito ![]()
![]()
![]()
![]()
Tabela najpomembnejših limit