4 Obratna (inverzna) matrika (II)
Spomnimo se, da je kvadratna matrika ![]() reda
reda ![]() obrnljiva, če obstaja njena inverzna matrika
obrnljiva, če obstaja njena inverzna matrika ![]() ; to pomeni, da je
; to pomeni, da je ![]() .
.
Izrek 4.1 [1,5]: Naj bo ![]() kvadratna matrika. Inverzna matrika
kvadratna matrika. Inverzna matrika ![]() obstaja natanko tedaj, ko je
obstaja natanko tedaj, ko je ![]() , in potem velja
, in potem velja
![]()
kjer je ![]() prirejenka matrike
prirejenka matrike ![]() ali adjungirana matrika matrike
ali adjungirana matrika matrike ![]() , definirana kot transponiranka matrike kofaktorjev elementov matrike
, definirana kot transponiranka matrike kofaktorjev elementov matrike ![]() , tj.
, tj.
![Rendered by QuickLaTeX.com \[B_A= \begin{pmatrix} k_{11}&k_{12}&\ldots&k_{1n}\\ k_{21}& k_{22}&\ldots& k_{2n}\\ \vdots&\vdots& &\vdots\\ k_{n1}& k_{n2}&\ldots& k_{nn} \end{pmatrix}^T.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-2cb995f3b56d6aa7c4e697e63bd7ffbf_l3.png)
Primer 4.1: Poiščimo inverzno matriko matrike ![]() .
.
Najprej izračunamo determinanto matrike ![]() :
: ![]() . Ker je
. Ker je ![]() , je matrika
, je matrika ![]() obrnljiva, torej obstaja
obrnljiva, torej obstaja ![]() .
.
Zdaj izračunamo kofaktorje elementov matrike ![]() :
:
![]()
Sledi, da je
![Rendered by QuickLaTeX.com \[A^{-1} =-\dfrac{1}{6} \cdot \begin{pmatrix} 1 & -2\\ -4& 2 \end{pmatrix}^T=\begin{pmatrix} -\dfrac{1}{6} & \dfrac{4}{6}\\ &\\ \dfrac{2}{6}& -\dfrac{2}{6} \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4bf54cdd898de6597a383d693ac2aa0c_l3.png)
Primer 4.2: Poiščimo inverzno matriko matrike 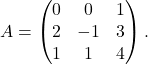
Izračunamo determinanto matrike ![]() z razvojem po prvi vrstici in dobimo
z razvojem po prvi vrstici in dobimo
![]() . Torej je matrika
. Torej je matrika ![]() obrnljiva. Zdaj izračunamo vse kofaktorje elementov matrike
obrnljiva. Zdaj izračunamo vse kofaktorje elementov matrike ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
Zdaj lahko zapišemo inverzno matriko:
![Rendered by QuickLaTeX.com \[A^{-1} =\dfrac{1}{3}\cdot \begin{pmatrix} -7 & 1 & 1 \\ -5 & -1 & 2\\ 3 & 0 & 0 \end{pmatrix}= \begin{pmatrix} -\dfrac{7}{3} & \dfrac{1}{3}& \dfrac{1}{3} \\ &&\\ -\dfrac{5}{3}& -\dfrac{1}{3} & \dfrac{2}{3}\\ &&\\ 1 & 0 & 0 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5d84b19b502c590990531f8673ddd16f_l3.png)
Primer 4.3: Dani sta matriki ![]() in
in ![]() . Poiščimo tako matriko
. Poiščimo tako matriko ![]() , da je
, da je ![]() .
.
Ker je ![]() , je matrika
, je matrika ![]() obrnljiva. Obe strani enačbe
obrnljiva. Obe strani enačbe ![]() lahko pomnožimo z
lahko pomnožimo z ![]() in dobimo
in dobimo
![]()
Ker je
![]() , dobimo
, dobimo
![]()
Primer 4.4: Rešimo matrično enačbo ![]() , kjer je
, kjer je
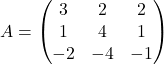 .
.
Najprej uredimo dano enačbo tako, da dobimo formulo za neznanko ![]() . Če
. Če ![]() izpostavimo, na levi strani dobimo
izpostavimo, na levi strani dobimo ![]() . Če je matrika
. Če je matrika ![]() obrnljiva, dobimo rešitev
obrnljiva, dobimo rešitev ![]() . V to formulo vstavimo matriko
. V to formulo vstavimo matriko ![]() in identično matriko
in identično matriko ![]() ter dobimo:
ter dobimo:
![Rendered by QuickLaTeX.com \[\begin{array}{lll}X&=& \left[ \begin{pmatrix} 3 & 1 & -2 \\ 2 & 4 & -4 \\ 2 & 1 & -1 \end{pmatrix} + \begin{pmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{pmatrix} \right]^{-1} \cdot\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4c1a50171a7cc689ea9c785bbc037c1a_l3.png)
![Rendered by QuickLaTeX.com \[\left[ \begin{pmatrix} 6 & 4 & 4 \\ 2 & 8 & 2 \\ -4 & -8 & -2 \end{pmatrix} + \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \right]\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-50073996292d141b3de6b2fb02f9f77e_l3.png)
![Rendered by QuickLaTeX.com \[&=& \begin{pmatrix} 5 & 1 & -2 \\ 2 & 6 & -4 \\ 2 & 1 & 2 \end{pmatrix}^{-1} \cdot \begin{pmatrix} 7 & 4 & 4 \\ 2 & 9 & 2 \\ -4 & -8 & -1 \end{pmatrix}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-edd88c493e976155ca1d45f34e1241e2_l3.png)
![Rendered by QuickLaTeX.com \[&=& \begin{pmatrix} \dfrac{2}{11} & -\dfrac{1}{22} & \dfrac{1}{11} \\ &&\\ -\dfrac{3}{22} & \dfrac{7}{44} & \dfrac{2}{11} \\ &&\\ -\dfrac{5}{44} & -\dfrac{3}{88} & \dfrac{7}{22} \end{pmatrix} \cdot \begin{pmatrix} 7 & 4 & 4 \\ 2 & 9 & 2 \\ -4 & -8 & -1 \end{pmatrix}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-7bc6945ed8f1cc6040f4130a0aac144e_l3.png)
![Rendered by QuickLaTeX.com \[=\begin{pmatrix} \dfrac{9}{11} & -\dfrac{9}{22} & \dfrac{6}{11} \\ &&\\ -\dfrac{15}{11} & -\dfrac{25}{44} & -\dfrac{9}{22} \\ &&\\ -\dfrac{47}{22} & -\dfrac{291}{88} & -\dfrac{37}{44} \end{pmatrix}. \end{array}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-94d2a08a9dab0efacac85904262a7e45_l3.png)
Računanje inverzne matrike z elementarnimi operacijami
Druga metoda za izračun inverzne matrike obrnljive matrike je uporaba tako imenovanih elementarnih operacij med vrsticami. Te operacije so:
 med seboj zamenjamo dve vrstici;
med seboj zamenjamo dve vrstici; vrstico pomnožimo z neničelnim realnim številom;
vrstico pomnožimo z neničelnim realnim številom;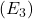 posamezni vrstici prištejemo večkratnik neke druge vrstice.
posamezni vrstici prištejemo večkratnik neke druge vrstice.
S simboli je zamenjava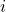 -te in
-te in 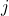 -te vrstice označena z
-te vrstice označena z 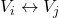 in množenje vrstice
in množenje vrstice 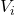 s konstanto
s konstanto  , kjer je
, kjer je 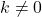 , z
, z 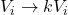 . Podobno prištetje
. Podobno prištetje  -kratnika
-kratnika 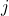 -te vrstice k
-te vrstice k 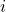 -ti vrstici označimo z
-ti vrstici označimo z 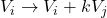 (na kratko pišemo
(na kratko pišemo 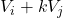 ).
).
Da bi izračunali inverzno matriko obrnljive matrike reda ![]() , sestavimo novo matriko velikosti
, sestavimo novo matriko velikosti ![]() tako, da dodamo identično matriko
tako, da dodamo identično matriko ![]() reda
reda ![]() na desni strani matrike
na desni strani matrike ![]() . Za novo matriko uporabimo elementarne operacije, da dobimo identično matriko na levi strani (kjer je bila
. Za novo matriko uporabimo elementarne operacije, da dobimo identično matriko na levi strani (kjer je bila ![]() na začetku), matrika na desni strani pa bo inverzna matrika matrike
na začetku), matrika na desni strani pa bo inverzna matrika matrike ![]() .
.
Najprej naredimo ničle v prvem stolpcu, na pozicijah pod glavno diagonalo, z uporabo elementarnih operacij med vrstico ![]() ,
, ![]() in
in ![]() . Ko naredimo ničle v drugem stolpcu, spet na pozicijah pod glavno diagonalo, bomo elementarne operacije uporabili med drugo vrstico in vrstico
. Ko naredimo ničle v drugem stolpcu, spet na pozicijah pod glavno diagonalo, bomo elementarne operacije uporabili med drugo vrstico in vrstico ![]() ,
, ![]() , ki jo bomo modificirali. Postopek nadaljujemo, dokler niso vsi elementi pod glavno diagonalo enaki
, ki jo bomo modificirali. Postopek nadaljujemo, dokler niso vsi elementi pod glavno diagonalo enaki ![]() . Nato postopek ponovimo za elemente nad glavno diagonalo, začenši z zadnjim stolpcem.
. Nato postopek ponovimo za elemente nad glavno diagonalo, začenši z zadnjim stolpcem.
Primer 4.5: Z uporabo elementarnih operacij med vrsticami poiščimo inverz matrike
![]()
Uporabimo zgornje elementarne operacije ![]() za matriko
za matriko ![]() .
.
Z naslednjo operacijo najprej naredimo ničlo na poziciji pod glavno diagonalo:
![]()
Po pretvorbi vseh elementov na glavni diagonali v ![]() naredimo ničle na pozicijah nad glavno diagonalo. V tem primeru moramo narediti ničlo na poziciji
naredimo ničle na pozicijah nad glavno diagonalo. V tem primeru moramo narediti ničlo na poziciji ![]() :
:
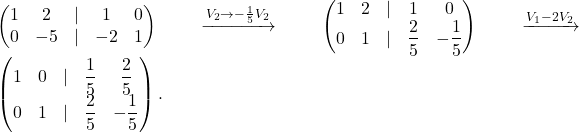
Na desni strani zadnje matrike preberemo inverzno matriko matrike ![]() :
:
![Rendered by QuickLaTeX.com \[A^{-1} = \begin{pmatrix} \dfrac{1}{5} & \dfrac{2}{5}\\ & \\ \dfrac{2}{5} & -\dfrac{1}{5} \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-8a06f75e6324724ddd66fdbcf6fc158a_l3.png)
Primer 4.6: Z uporabo elementarnih operacij poiščimo inverz matrike
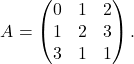
Najprej napišemo novo matriko ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{pmatrix} 0 & 1 & 2&\lvert&1&0&0\\ 1 & 2 & 3&\lvert&0&1&0\\ 3 & 1 & 1&\lvert&0&0&1 \end{pmatrix}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-493defce5f85b8babaff490b80db23ef_l3.png)
Ker morajo biti na glavni diagonali matrike v levem bloku vsi elementi enaki ![]() , najprej zamenjamo vrstico
, najprej zamenjamo vrstico ![]() z vrstico
z vrstico ![]() , torej naredimo operacijo
, torej naredimo operacijo ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{pmatrix} 1 & 2 & 3&\lvert&0&1&0\\ 0 & 1 & 2&\lvert&1&0&0\\ 3 & 1 & 1&\lvert&0&0&1 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-22ed3857761f832bcfec426853e95ef6_l3.png)
Pod glavno diagonalo začnemo oblikovati ničle:
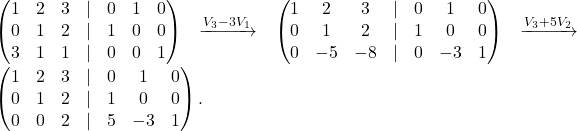
Ko ustvarimo ![]() na poziciji
na poziciji ![]() , ponovimo postopek pridobivanja ničel nad glavno diagonalo matrike, zapisane v levem bloku: najprej v tretjem stolpcu, nato pa v drugem:
, ponovimo postopek pridobivanja ničel nad glavno diagonalo matrike, zapisane v levem bloku: najprej v tretjem stolpcu, nato pa v drugem:
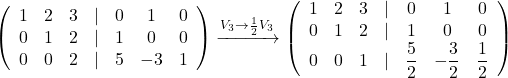
![Rendered by QuickLaTeX.com \xrightarrow[V_1-3V_3] {V_2-2V_3}\begin{pmatrix} 1 & 2 & 0&\lvert&-\dfrac{15}{2}&\dfrac{11}{2}&-\dfrac{3}{2}\\ 0 & 1 & 0&\lvert&-4&3&-1\\ 0 & 0 & 1&\lvert&\displaystyle\dfrac{5}{2}&-\displaystyle\frac{3}{2}&\displaystyle\frac{1}{2} \end{pmatrix}\xrightarrow {V_1-2V_2}\begin{pmatrix} 1 & 0 & 0&\lvert&\dfrac{1}{2}&-\dfrac{1}{2}&\dfrac{1}{2}\\ 0 & 1 & 0&\lvert&-4&3&-1\\ 0 & 0 & 1&\lvert&\dfrac{5}{2}&-\dfrac{3}{2}&\dfrac{1}{2} \end{pmatrix}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-56a42f9846fb4e774f16eabfc03c6070_l3.png) .
.
Torej je 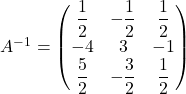 .
.
Primer 4.7: Poiščimo inverz matrike
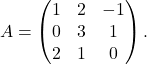
Z naslednjim zaporedjem operacij
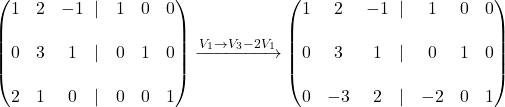
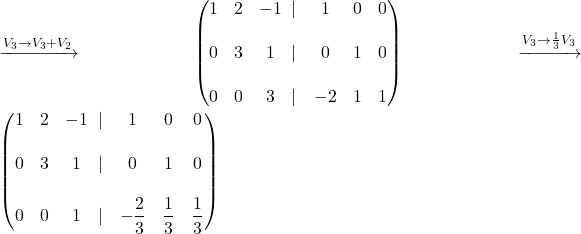
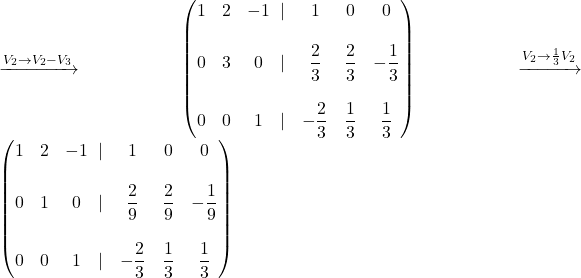
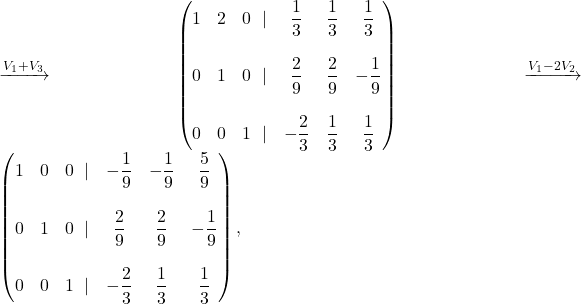
dobimo, da je inverzna matrika matrike ![]() enaka
enaka 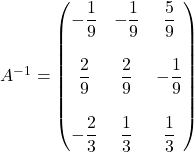 .
.