14 Definicija in geometrijski pomen odvoda
Naj bo funkcija ![]() definirana na intervalu
definirana na intervalu ![]() . Naj bo
. Naj bo ![]() notranja točka intervala
notranja točka intervala ![]() . Radi bi razumeli, kako hitro se spreminja vrednost
. Radi bi razumeli, kako hitro se spreminja vrednost ![]() glede na vrednost točke
glede na vrednost točke ![]() .
.
Izraz ![]() imenujemo diferenčni kvocient in je enak naklonskemu koeficientu premice skozi točki
imenujemo diferenčni kvocient in je enak naklonskemu koeficientu premice skozi točki ![]() in
in ![]() .
.
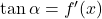 .
.Definicija 14.1: Funkcija ![]() je odvedljiva v točki
je odvedljiva v točki ![]() , če obstaja limita
, če obstaja limita
![]()
Vrednost te limite označimo z ![]() in jo imenujemo odvod funkcije f v točki
in jo imenujemo odvod funkcije f v točki ![]() . Rečemo, da je funkcija
. Rečemo, da je funkcija ![]() odvedljiva na intervalu
odvedljiva na intervalu ![]() , če je odvedljiva v vsaki njegovi točki.
, če je odvedljiva v vsaki njegovi točki.
Primer 14.1: Z uporabo definicije poiščite odvod funkcije ![]() .
.
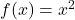 .
.
Po definiciji izračunamo:
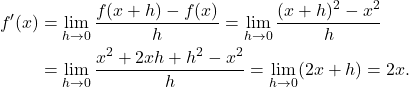
To pomeni, da je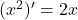 .
.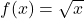 .
.
Izračunamo: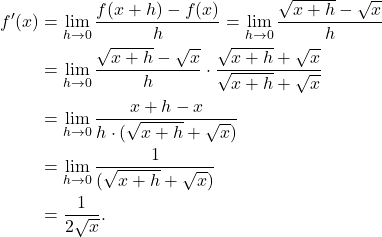
Torej smo ugotovili, da je
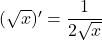 .
.
Primer 14.2: Ali je funkcija ![]() odvedljiva v točki
odvedljiva v točki ![]() ?
?
Ker je 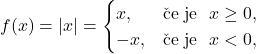 moramo izračunati levo in desno limito v točki
moramo izračunati levo in desno limito v točki ![]() :
:
![]()
in podobno
![]()
Ker desni in levi limiti nista enaki, sklepamo, da ne obstaja ![]() , to pomeni, da ne obstaja
, to pomeni, da ne obstaja ![]() .
.
Definicija 14.2: Naj bo funkcija ![]() definirana na intervalu
definirana na intervalu ![]() .
.
- Če obstaja
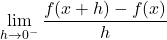 , pravimo, da je funkcija
, pravimo, da je funkcija  z leve odvedljiva v točki
z leve odvedljiva v točki  , in vrednost te limite označimo z
, in vrednost te limite označimo z 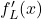 . Funkcijo
. Funkcijo 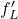 imenujemo levi odvod funkcije
imenujemo levi odvod funkcije  .
. - Če obstaja
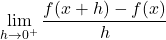 , pravimo, da je funkcija
, pravimo, da je funkcija  z desne odvedljiva v točki
z desne odvedljiva v točki  , in vrednost te limite označimo z
, in vrednost te limite označimo z 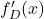 . Funkcijo
. Funkcijo 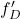 Imenujemo desni odvod funkcije
Imenujemo desni odvod funkcije  .
.
Izrek 14.1 [10]: Funkcija ![]() je odvedljiva v točki
je odvedljiva v točki ![]() natanko tedaj, ko je v tej točki odvedljiva z leve in z desne in sta levi in desni odvod v tej točki enaka.
natanko tedaj, ko je v tej točki odvedljiva z leve in z desne in sta levi in desni odvod v tej točki enaka.
Izrek 14.2 [10]: Če je funkcija ![]() v točki
v točki ![]() odvedljiva, je v tej točki tudi zvezna.
odvedljiva, je v tej točki tudi zvezna.
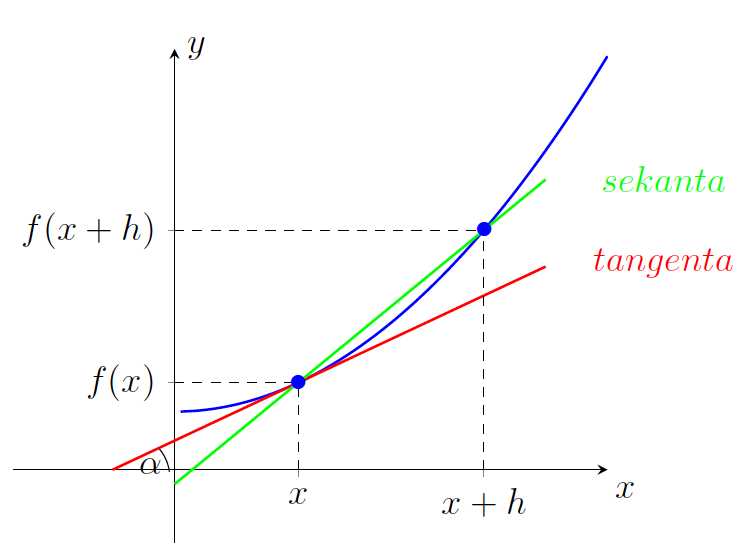
Geometrijski pomen odvoda
Naj bo zvezna funkcija ![]() definirana na intervalu
definirana na intervalu ![]() . Premica skozi točki
. Premica skozi točki ![]() in
in ![]() na sliki 14.1 se imenuje sekanta. Ko se
na sliki 14.1 se imenuje sekanta. Ko se ![]() približuje vrednosti
približuje vrednosti ![]() , se točka
, se točka ![]() približuje točki
približuje točki ![]() . Sekanto v limitni legi imenujemo tangenta na krivuljo v točki
. Sekanto v limitni legi imenujemo tangenta na krivuljo v točki ![]()
Tangenta na graf funkcije ![]() v točki
v točki ![]() s pozitivnim poltrakom abscisne osi oklepa kot
s pozitivnim poltrakom abscisne osi oklepa kot ![]() in
in
![]()
Enačba tangente na graf funkcije v točki ![]() je
je
![]()