19 Risanje grafov funkcij
Pri risanju grafov funkcij poiščemo ali izračunamo naslednje elemente:
- domeno
 ali definicijsko območje;
ali definicijsko območje; - eventualne ničle in pole;
- limite (na robu definicijskega območja) in eventualne asimptote (vodoravne, poševne, navpične);
- eventualne stacionarne točke in lokalne ekstreme;
- intervale naraščanja in padanja funkcij;
- prevoje ter intervale konveksnosti in konkavnosti funkcij.
Primer 19.1: Skicirajmo graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]() .
.
- Dana funkcija je racionalna, torej je definirana, kjer je imenovalec različen od
 . V našem primeru, to je
. V našem primeru, to je 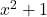 , je pri
, je pri  vedno različen od
vedno različen od  . Torej je domena funkcje:
. Torej je domena funkcje: 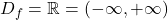 .
. - Ničle racionalne funkcije so ničle števca, torej je
![Rendered by QuickLaTeX.com \[f(x) = 0 \Longleftrightarrow 2x=0 \Longleftrightarrow x=0.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-a686acf5b3ebb317339522c25c7d69ee_l3.png)
Poli so ničle imenovalca. V našem primeru funkcija nima polov.
- Poiščemo vse eventualne asimptote.
I) Ker funkcija nima polov, nima niti navpičnih asimptot.
II) Zdaj izračunamo limite dane funkcije, ko gre proti
proti 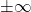 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \frac{2x}{x^2+1} = 0^+\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-eae65cbb2caadc86e72b1d168d1de0e7_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} \frac{2x}{x^2+1} = 0^-\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-36ab62d64784cad3c55dffc32c7cbd3d_l3.png)
Torej, premica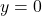 je vodoravna asimptota.
je vodoravna asimptota.
III) Funkcija nima poševnih asimptot, ker ima vodoravno asimptoto. - Poiščemo stacionarne točke. To so ničle prvega odvoda:
![Rendered by QuickLaTeX.com \[f'(x) = \frac{(2x)' \cdot (x^2+1) - 2x \cdot (x^2+1)'}{(x^2+1)^2} = \frac{2x^2+2-4x^2}{(x^2+1)^2}=\frac{-2x^2+2}{(x^2+1)^2}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-9cda2b57f8c3acfb766b0adc992b2067_l3.png)
Ker je
![Rendered by QuickLaTeX.com \[f'(x) = 0 \Longleftrightarrow -2x^2+2 =-2\cdot (x^2-1)=0 \Longleftrightarrow x^2-1=0,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4d713d5f550925c909d963718d9c5701_l3.png)
sta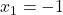 in
in 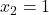 stacionarni točki.
stacionarni točki.
Zdaj izračunamo vrednost drugega odvoda funkcije v stacionarnih točkah. Ker je
v stacionarnih točkah. Ker je
![Rendered by QuickLaTeX.com \[f''(x) {=} \left(\frac{-2x^2+2}{(x^2+1)^2}\right)' {=} \frac{-4x \cdot (x^2+1)^2 - (-2x^2+2) \cdot (2\cdot (x^2+1) \cdot 2x)}{(x^2+1)^4}{=}\frac{4x(x^2-3)}{(x^2+1)^3},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-c429d5dcc9fbecbfa2363d5f00acc519_l3.png)
dobimo
![Rendered by QuickLaTeX.com \[f''(-1) = \frac{4\cdot (-1) \cdot(-2)}{2^3} >0,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-f5ab7d98de9aa98e4bc8041a38d7f520_l3.png)
kar pomeni, da je v točki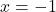 lokalni minimum ter je
lokalni minimum ter je
![Rendered by QuickLaTeX.com \[f''(1) = \frac{4\cdot 1\cdot(-2)}{2^3} <0,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-8bad03faa9e2ca4a7ec0a84c6a6bc9cf_l3.png)
zato je v točki lokalni maksimum. Poiščemo tudi prevoje in dobimo
lokalni maksimum. Poiščemo tudi prevoje in dobimo 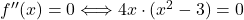 , torej so točke
, torej so točke  ,
, 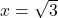 in
in 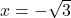 prevoji funkcije.
prevoji funkcije. - Najprej preštudiramo predznak prvega odvoda
![Rendered by QuickLaTeX.com \[f'(x)=\frac{-2x^2+2}{(x^2+1)^2}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-914bc098e9248ba971eb9dd2058db3a1_l3.png)
Števec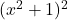 je povsod pozitiven, imenovalec pa je polinom stopnje
je povsod pozitiven, imenovalec pa je polinom stopnje  , torej je njegov graf parabola (glej sliko 19.1). To je konkavna parabola, ker je vodilni koeficient, tj.
, torej je njegov graf parabola (glej sliko 19.1). To je konkavna parabola, ker je vodilni koeficient, tj. 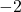 , negativen.
, negativen.

Slika 19.1: Graf polinomske funkcije 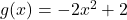 .
.Preštudiramo še predznak drugega odvoda, ki je podan le s predznakom števca, saj je imenovalec
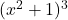 pozitiven za vse
pozitiven za vse  v domeni funkcije.
v domeni funkcije.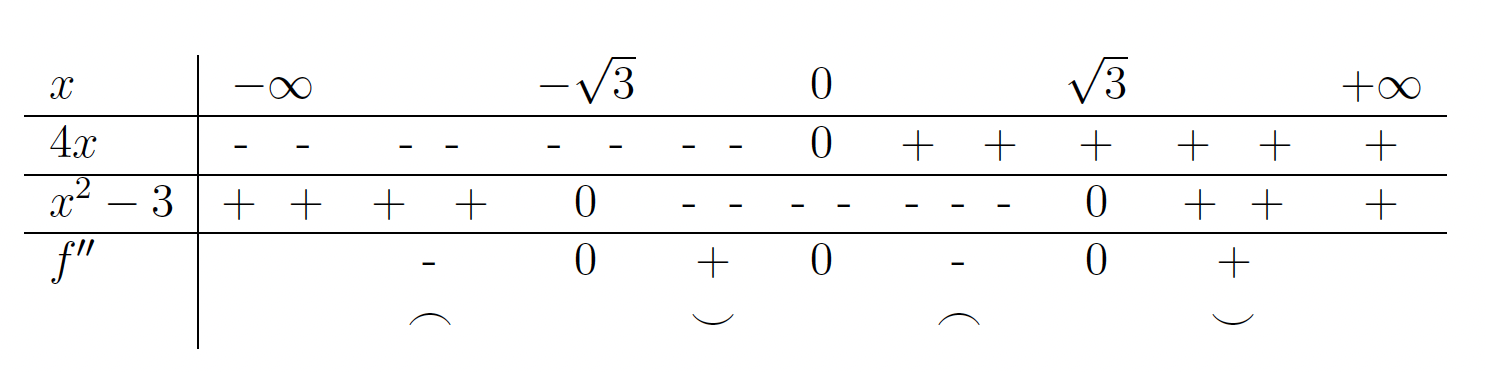
- V naslednji tabeli bomo povzeli vse podatke, ki smo jih pridobili v prejšnjih točkah, in ugotovili intervale naraščanja oziroma padanja ter konveksnosti oziroma konkavnosti funkcije
 .
.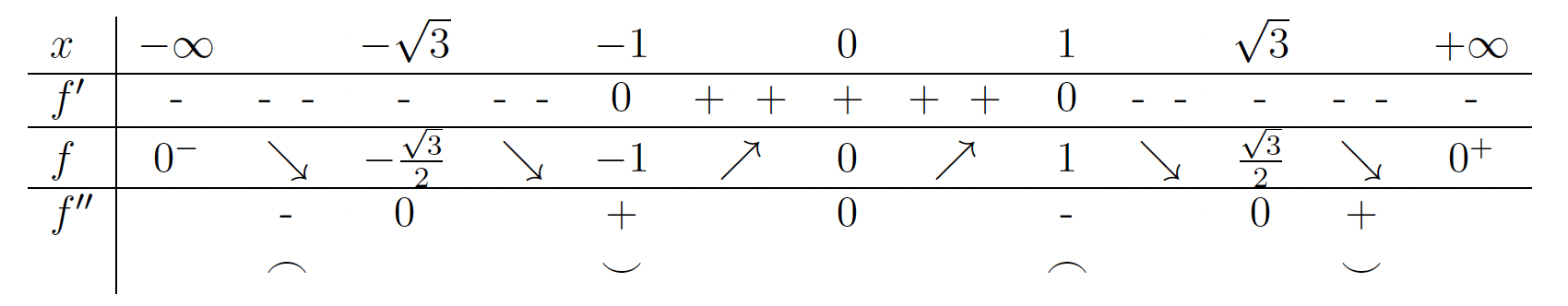
Funkcija je naraščajoča na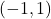 ter padajoča na
ter padajoča na 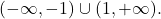 Poleg tega vidimo, da je funkcija konveksna na
Poleg tega vidimo, da je funkcija konveksna na 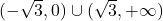 in konkavna na
in konkavna na 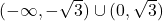 .
. - Na podlagi prejšnje tabele bomo narisali graf funkcije (glej sliko 19.2).
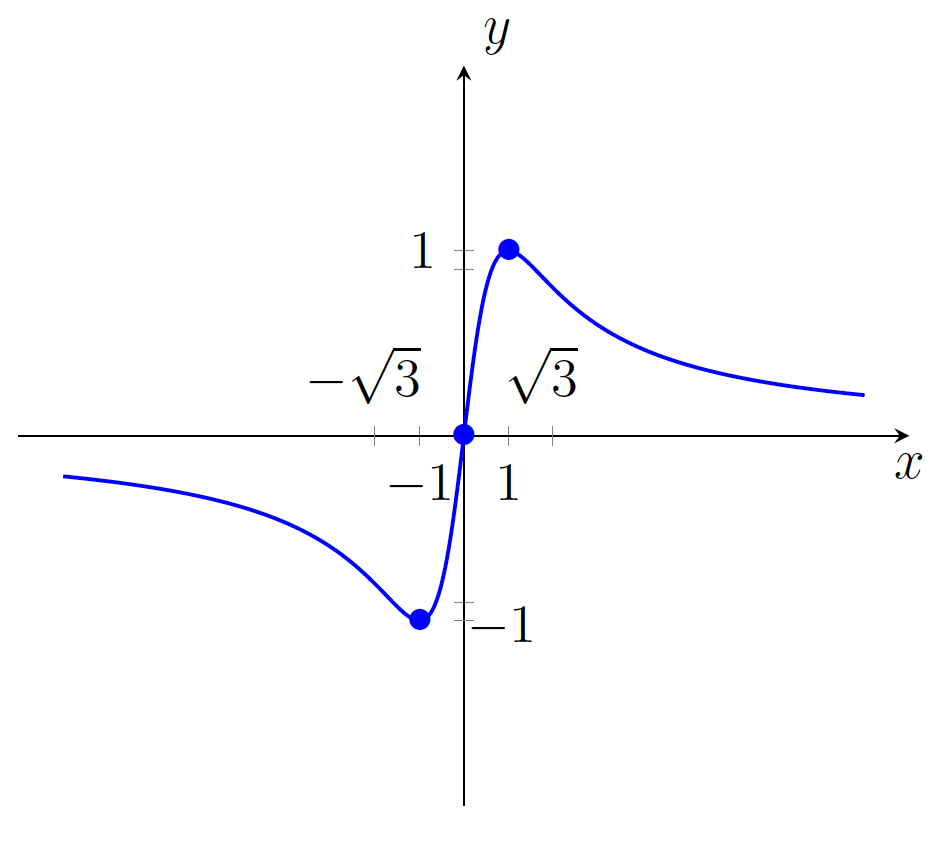
Slika 19.2: Graf racionalne funkcije 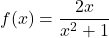 .
.
Primer 19.2: Skicirajmo graf funkcije ![]() , podane s predpisom
, podane s predpisom ![]()
- Dana funkcija je polinomska funkcija, torej je povsod definirana in je njena domena
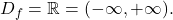
- Ničle funkcije so rešitve enačbe
![Rendered by QuickLaTeX.com \[f(x) = 0 \Longleftrightarrow (x^2-9) \cdot (x^2-1)=(x-3)\cdot (x+3)\cdot (x-1)\cdot (x+1)=0.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-12a8b12f0344ee8b486140a9f242a100_l3.png)
Torej ima fukcija ničle:
ničle: 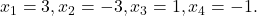 Funkcija nima polov.
Funkcija nima polov. - Poiščemo vse eventualne asimptote.
I) Ker funkcija nima polov, nima niti navpičnih asimptot.
II) Zdaj izračunamo limite dane funkcije, ko gre proti
proti 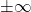 :
:
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \frac{1}{4} \cdot (x^2-9) \cdot (x^2-1) = +\infty,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-da68cbf3844878ca47c912a640f95b33_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} \frac{1}{4} \cdot (x^2-9) \cdot (x^2-1) = +\infty.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-e79fea5c1656d75b14fbf17449103e44_l3.png)
To pomeni, da funkcija nima vodoravnih asimptot.
III) Ugotoviti moramo, ali ima funkcija poševno asimptoto, zato izračunamo
![Rendered by QuickLaTeX.com \[\lim_{x \to \pm\infty} \frac{f(x)}{x} = +\infty,\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-cb9d1af2f03da12455b3b1f777cbe03a_l3.png)
kar pomeni, da funkcija nima niti poševne asimptote. - Poiščemo stacionarne točke. To so ničle prvega odvoda s predpisom
![Rendered by QuickLaTeX.com \[f'(x) = \frac{1}{4}\cdot [ 2x \cdot (x^2-1) + (x^2-9) \cdot 2x] = \frac{1}{2} x \cdot (2x^2-10)= x \cdot (x^2-5).\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-279509164657b73d526f321b5d6809cb_l3.png)
Ker je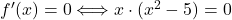 , sledi, da so stacionarne točke
, sledi, da so stacionarne točke 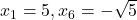 in
in 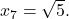
- Zdaj izračunamo vrednost drugega odvoda funkcije
 v stacionarnih točkah.
v stacionarnih točkah.
Še enkrat odvajamo prvi odvod funkcije in dobimo
in dobimo 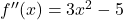 . Sledi, da je
. Sledi, da je 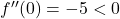 , kar pomeni, da je v točki
, kar pomeni, da je v točki 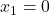 lokalni maksimum. Ker je
lokalni maksimum. Ker je 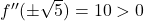 , ugotovimo, da sta v točkah
, ugotovimo, da sta v točkah 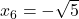 in
in 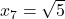 lokalna minimuma.
lokalna minimuma. - Poiščemo tudi prevoje in dobimo
![Rendered by QuickLaTeX.com \[f''(x) = 0 \Longleftrightarrow 3x^2-5=0 \Longleftrightarrow x = \pm \sqrt{\frac{5}{3}}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-e623c60de661de51e14cc16aa800616d_l3.png)
Torej, točki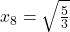 in
in 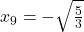 sta prevoja funkcije
sta prevoja funkcije  .
. - V naslednji tabeli bomo povzeli vse podatke, ki smo jih pridobili v prejšnjih točkah, in ugotovili intervale naraščanja oziroma padanja funkcije
 . Najprej izračunamo še nekaj vrednosti funkcije
. Najprej izračunamo še nekaj vrednosti funkcije  :
:
![Rendered by QuickLaTeX.com \[f(-\sqrt{5})=\frac{1}{4}\cdot (5-9)\cdot (5-1)=-4=f(\sqrt{5}), f(0)=\frac{1}{4}\cdot (0-9)\cdot (0-1)=\frac{9}{4}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-074876180e3a758f83d8903d43139696_l3.png)
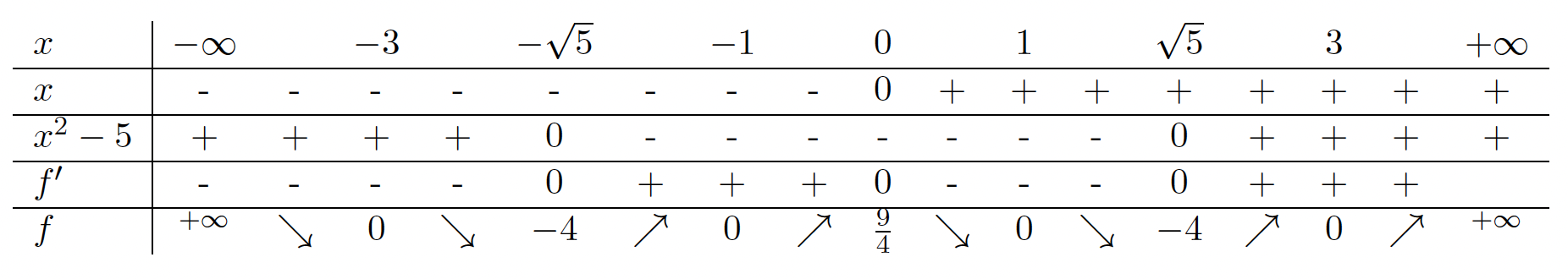 Funkcija
Funkcija  je naraščajoča na uniji intervalov
je naraščajoča na uniji intervalov ![Rendered by QuickLaTeX.com [-\sqrt{5}, 0]\cup [\sqrt{5}, +\infty)](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-aaf59a129c656f07fe7181ff2aa8e64f_l3.png) ter padajoča na uniji intervalov
ter padajoča na uniji intervalov ![Rendered by QuickLaTeX.com (-\infty, -\sqrt{5}]\cup [0, \sqrt{5}]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-248f05719fd3211b8784486928fd38d9_l3.png) .
. - Na podlagi prejšnje tabele bomo narisali graf funkcije (glej sliko 19.3).
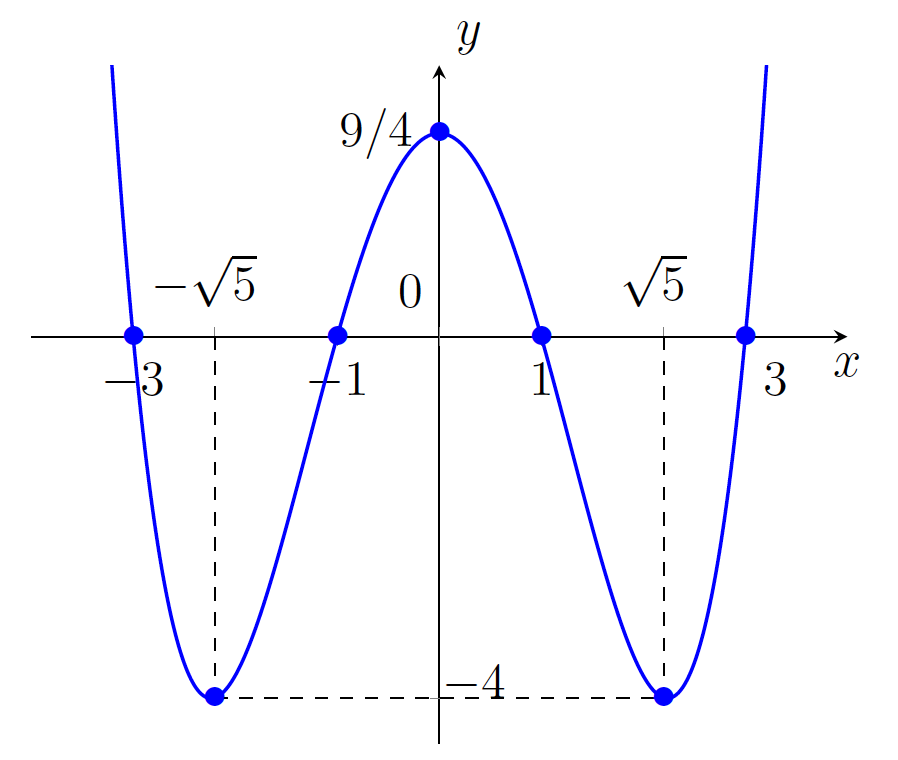
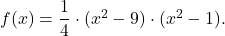
Ker vemo, da sta prevoja enaka ![]() , z grafa funkcije razberemo, da je funkcija konveksna na uniji intervalov
, z grafa funkcije razberemo, da je funkcija konveksna na uniji intervalov ![]() ter konkavna na intervalu
ter konkavna na intervalu ![]() .
.