5 Sistemi linearnih enačb
Sistem ![]() linearnih enačb z
linearnih enačb z ![]() neznankami
neznankami ![]() je množica enačb
je množica enačb
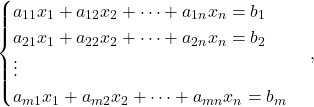
ki jih lahko zapišemo v matrični obliki kot ![]() , kjer je
, kjer je ![]() matrika koeficientov sistema,
matrika koeficientov sistema,  stolpec
stolpec ![]() neznank ter
neznank ter 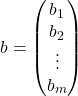 stolpec
stolpec ![]() desnih strani sistema.
desnih strani sistema.
Cramerjevo pravilo
To je posebna metoda za reševanje sistemov linearnih enačb s toliko enačbami kot neznankami, torej ko je matrika koeficientov kvadratna in obrnljiva.
Izrek 5.1 [1,5]: Če je ![]() kvadratna matrika z
kvadratna matrika z ![]() , je sistem enolično rešljiv in rešitve so
, je sistem enolično rešljiv in rešitve so
![]()
kjer je ![]() determinanta matrike
determinanta matrike ![]() ,
, ![]() , ki jo dobimo tako, da v matriki
, ki jo dobimo tako, da v matriki ![]() zamenjamo
zamenjamo ![]() -ti stolpec s stolpcem desnih strani
-ti stolpec s stolpcem desnih strani ![]() .
.
Primer 5.1: Rešimo naslednji sistem:
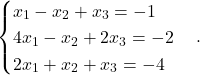
Matrika koeficientov je 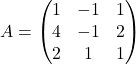 in stolpec desnih strani je
in stolpec desnih strani je 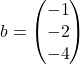 . Najprej se lotimo računanja determinante matrike
. Najprej se lotimo računanja determinante matrike ![]() , da preverimo, ali je različna od nič, in dobimo
, da preverimo, ali je različna od nič, in dobimo 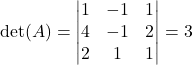 . To pomeni, da lahko uporabimo Cramerjevo pravilo. Izračunamo še
. To pomeni, da lahko uporabimo Cramerjevo pravilo. Izračunamo še
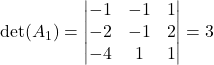 ,
, 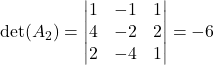 in
in
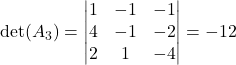 . Torej je rešitev sistema
. Torej je rešitev sistema
![]() ,
, ![]() ter
ter
![]() .
.
Gaussova eliminacijska metoda
Pri tej metodi neznanke iz enačb sistematično izločimo tako, da dobimo zgornjetrikotno obliko sistema.
Primer 5.2: Rešimo naslednji sistem:
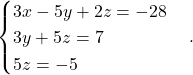
Sistem linearnih enačb, ki je v zgornjetrikotni obliki, kot je dani sistem, rešimo od zadnje enačbe proti prvi (torej od najpreprostejše k najzahtevnejši). Torej iz tretje enačbe takoj izračunamo ![]() . Vrednost neznanke
. Vrednost neznanke ![]() vstavimo v drugo enačbo sistema in izračunamo
vstavimo v drugo enačbo sistema in izračunamo ![]() . Ker je
. Ker je ![]() , dobimo
, dobimo ![]() . Potem vrednosti neznank
. Potem vrednosti neznank ![]() in
in ![]() vstavimo v prvo enačbo sistema in izračunamo
vstavimo v prvo enačbo sistema in izračunamo ![]() . Iz enačbe
. Iz enačbe ![]() sledi, da je
sledi, da je ![]() .
.
Naj bo sistem ![]() . Če matriki
. Če matriki ![]() dodamo še stolpec
dodamo še stolpec ![]() , dobimo novo matriko reda
, dobimo novo matriko reda ![]() , ki ji pravimo razširjena matrika sistema, označimo jo z
, ki ji pravimo razširjena matrika sistema, označimo jo z
![Rendered by QuickLaTeX.com \[\widetilde A=\begin{pmatrix} a_{11} & a_{12} &\cdots& a_{1n} & \lvert & b_1\\ a_{21} & a_{22} &\cdots& a_{2n} & \lvert & b_2\\ \cdots&\cdots&\cdots & \cdots& \lvert& \cdots\\ a_{m1} & a_{m2} &\cdots& a_{mn} & \lvert & b_m \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-92730086f8cd0f4a341a2e58f4af47f4_l3.png)
Sistem rešujemo tako, da z operacijami, ki na rešitve sistema ne vplivajo, spreminjamo enačbe, dokler niso zapisane v zgornjetrikotni obliki. Takšne operacije so:
- poljubni enačbi zamenjamo;
- poljubno enačbo na levi in desni strani pomnožimo (ali delimo) s poljubnim neničelnim številom;
- poljubni enačbi prištejemo (ali od nje odštejemo) drugo enačbo, pomnoženo z nekim od
 različnim številom.
različnim številom.
Pri matriki ![]() so te operacije:
so te operacije:
- poljubni vrstici zamenjamo;
- poljubno vrstico pomnožimo (ali delimo) s poljubnim neničelnim številom;
- poljubni vrstici prištejemo (ali od nje odštejemo) drugo vrstico, pomnoženo z nekim neničelnim številom.
Gornje operacije imenujemo elementarne vrstične operacije. S temi operacijami dobimo ničle pod glavno diagonalo matrike ![]() . Ta oblika se imenuje vrstična kanonična oblika in ima naslednji lastnosti:
. Ta oblika se imenuje vrstična kanonična oblika in ima naslednji lastnosti:
- za neko naravno število
 je prvih
je prvih  vrstic matrike
vrstic matrike 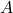 neničelnih, zadnjih
neničelnih, zadnjih 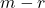 vrstic pa vsebuje samo ničle;
vrstic pa vsebuje samo ničle; - v prvih
 neničelnih vrsticah imenujemo prvi neničelni element vsake vrstice pivot. Za dve zaporedni vrstici vedno velja, da je pivot v spodnji vrstici bolj desno od pivota v zgornji vrstici.
neničelnih vrsticah imenujemo prvi neničelni element vsake vrstice pivot. Za dve zaporedni vrstici vedno velja, da je pivot v spodnji vrstici bolj desno od pivota v zgornji vrstici.
Primer 5.3: Rešimo naslednji sistem:
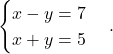
Razširjena matrika tega sistema je
![]() .
.
Prvi korak: Po potrebi zamenjamo prvo vrstico s kako drugo tako, da v zgornjem levem vogalu dobimo neničelni element (pri računanju peš je najbolje, da je to enica). Temu elementu bomo rekli pivot. V našem primeru je že enica.
Drugi korak: Z uporabo elementarnih vrstičnih operacij naredimo ničle v prvem stolpcu pod pivotom.
![]()
Razširjena matrika ima že vrstično kanonično obliko.
Tretji korak: Zadnji matriki sedaj priredimo nazaj sistem linearnih enačb:
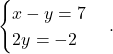
Jasno je, da je ![]() , in potem iz prve enačbe dobimo
, in potem iz prve enačbe dobimo ![]() oziroma
oziroma ![]() .
.
Primer 5.4: Rešimo naslednji sistem:
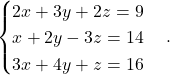
Razširjena matrika sistema je 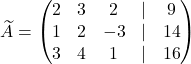 .
.
Ker imamo v zgornjem levem vogalu ![]() , zamenjamo prvo vrstico z drugo in dobimo ekvivalentno matriko
, zamenjamo prvo vrstico z drugo in dobimo ekvivalentno matriko
![Rendered by QuickLaTeX.com \[\widetilde A=\begin{pmatrix} \fbox{1}& 2 & -3&\lvert &14\\ 2& 3 &2& \lvert &9\\ 3& 4& 1&\lvert &16 \end{pmatrix}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-b541a939425f6a08b5a497990904ff36_l3.png)
in zdaj je pivot ![]() . Z operacijami
. Z operacijami ![]() in
in ![]() pod pivotom v prvem stolpcu naredimo ničli. Nova matrika je
pod pivotom v prvem stolpcu naredimo ničli. Nova matrika je
![Rendered by QuickLaTeX.com \[\widetilde A=\begin{pmatrix} 1& 2 & -3&\lvert &-14\\ 0& \fbox{-1} &8& \lvert &-19\\ 0& -2& 10&\lvert &-26 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-cbc261c85c7311bc36dcf350b6f81f09_l3.png)
Postopek nadaljujemo pri sledečem delu matrike, pri čemer odmislimo prvo vrstico in prvi stolpec. Zdaj je pivot ![]() in z operacijo
in z operacijo ![]() pod njim naredimo ničlo. Dobimo matriko
pod njim naredimo ničlo. Dobimo matriko
![Rendered by QuickLaTeX.com \[\widetilde A=\begin{pmatrix} 1& 2 & -3&\lvert &14\\ 0& -1 &8& \lvert &-19\\ 0& 0& -6&\lvert &12 \end{pmatrix},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-3eefadf7131aeb675d64f2af103a0844_l3.png)
ki je vrstična kanonična oblika razširjene matrike ![]() . Tej matriki sedaj priredimo sistem linearnih enačb:
. Tej matriki sedaj priredimo sistem linearnih enačb:

Iz tretje enačbe sledi, da je ![]() . Vstavimo vrednost neznanke
. Vstavimo vrednost neznanke ![]() v drugo vrstico in izračunamo
v drugo vrstico in izračunamo ![]() . Ker je
. Ker je ![]() , sledi, da je
, sledi, da je ![]() . Vrednosti neznank
. Vrednosti neznank ![]() in
in ![]() vstavimo v prvo vrstico in izračunamo
vstavimo v prvo vrstico in izračunamo ![]() . To pomeni
. To pomeni ![]() oziroma
oziroma ![]() .
.
Splošni algoritem, uporabljen prej, imenujemo Gaussova eliminacijska metoda.
Primer 5.5: Rešimo naslednji sistem:
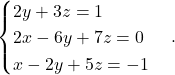
Z metodo Gaussove eliminacije razširjeno matriko ![]() preoblikujemo v vrstično kanonično obliko:
preoblikujemo v vrstično kanonično obliko:
![Rendered by QuickLaTeX.com \[\widetilde A=\begin{pmatrix} 0& 2& 4 &\lvert &1\\ 2& -6& 7& \lvert &0\\ 1& -2& 5& \lvert& -1 \end{pmatrix}\overset{V_1\leftrightarrow V_3}{\sim} \begin{pmatrix} \fbox{1}& -2& 5 &\lvert &-1\\ 2& -6& 7& \lvert &0\\ 0& 2& 3& \lvert& 1 \end{pmatrix}\overset{V_2-2 V_1}{\sim}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-eb049e383f1cfed2831684ab40f6362b_l3.png)
![Rendered by QuickLaTeX.com \[\begin{pmatrix} 1& -2& 5 &\lvert &-1\\ 0& \fbox{-2}& 3& \lvert &2\\ 0& 2& 3& \lvert& 1 \end{pmatrix}\overset{V_3+ V_2}{\sim} \begin{pmatrix} 1& -2& 5 &\lvert &-1\\ 0& -2& -3& \lvert &2\\ 0& 0& 0& \lvert& 3 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-f17eff53cd75ad993dd2bc44c407609b_l3.png)
Pripadajoči sistem je
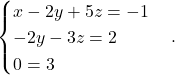
Zadnja enačba je protislovje, kar pomeni, da sistem ni rešljiv.
Primer 5.6: Rešimo naslednji sistem:
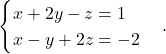
Z uporabo Gaussove metode preoblikujemo razširjeno matriko sistema v ustrezno obliko:
![]()
Priredimo sistem linearnih enačb
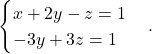
V zadnji enačbi sta dve neznanki, zato izberemo na primer ![]() , kjer je
, kjer je ![]() poljubno realno število. Potem izračunamo
poljubno realno število. Potem izračunamo ![]() . Iz enačbe
. Iz enačbe ![]() sledi, da je
sledi, da je ![]() .
.
Vrednosti neznank ![]() in
in ![]() vstavimo v prvo enačbo
vstavimo v prvo enačbo
![]()
in izračunamo vrednost neznanke ![]() . Dobimo
. Dobimo ![]() .
.
Ker je neskončno mnogo možnosti za izbor vrednosti parametra ![]() , ima sistem neskončno mnogo rešitev. Recimo, da je sistem neskončno rešljiv.
, ima sistem neskončno mnogo rešitev. Recimo, da je sistem neskončno rešljiv.
Rešljivost sistemov
Z uporabo Gaussove eliminacijske metode lahko iz poljubne neničelne matrike ![]() reda
reda ![]() pridobimo vrstično kanonično obliko te matrike. Vsaka matrika ima enolično določeno vrstično kanonično obliko, ki ni odvisna od zaporedja izvedenih elementarnih vrstičnih operacij.
pridobimo vrstično kanonično obliko te matrike. Vsaka matrika ima enolično določeno vrstično kanonično obliko, ki ni odvisna od zaporedja izvedenih elementarnih vrstičnih operacij.
Definicija 5.1: Rang matrike ![]() (oznaka
(oznaka ![]() ali
ali ![]() ) je maksimalno število neničelnih vrstic, ki jih dobimo z Gaussovo eliminacijsko metodo, oziroma
) je maksimalno število neničelnih vrstic, ki jih dobimo z Gaussovo eliminacijsko metodo, oziroma ![]() je število pivotov v vrstični kanonični obliki matrike
je število pivotov v vrstični kanonični obliki matrike ![]() .
.
Če je ![]() matrika reda
matrika reda ![]() , vselej velja, da je
, vselej velja, da je ![]() .
.
Če je ![]() matrika reda
matrika reda ![]() , je
, je ![]() natanko tedaj, ko je
natanko tedaj, ko je ![]() .
.
Velja tudi:
-
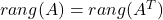 ;
; -
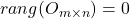 ;
; -
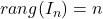 .
.
Primer 5.7: Izračunajmo rang matrike
![Rendered by QuickLaTeX.com \[A = \begin{pmatrix} 1 & 2 & 3 & 4\\ -1 & -2 & 1& 0\\ 2 & 1 & 1 & 4 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-8112e44654ed768eb0a9ea76fa5c14e0_l3.png)
Preoblikujemo dano matriko v vrstično kanonično obliko:
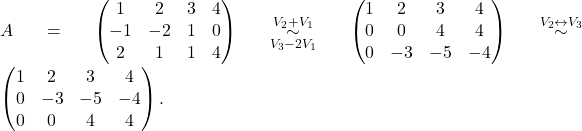
Ker dobimo ![]() neničelne vrstice, je
neničelne vrstice, je ![]()
Primer 5.8: Izračunajmo rang matrike
![Rendered by QuickLaTeX.com \[A = \begin{pmatrix} 4 & -2 & 1 & 1\\ -1 & 1 & -2 & 5\\ -8 & 4 & -2 & -2 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-7b98f5123d6a5a5bfc5426ce74c11e54_l3.png)
Spet z uporabo elementarnih vrstičnih operacij preoblikujemo dano matriko v vrstično kanonično obliko:
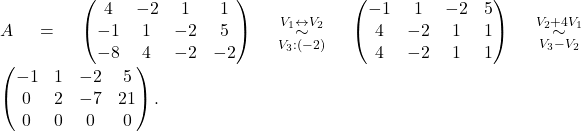
V tem primeru smo dobili dve neničelni vrstici, torej je ![]()
Zdaj lahko predstavimo splošni izrek za reševanje poljubnega sistema linearnih enačb.
Izrek 5.2 [1,5]: Naj bo ![]() sistem
sistem ![]() linearnih enačb z
linearnih enačb z ![]() neznankami in
neznankami in ![]() je razširjena matrika tega sistema. Potem velja:
je razširjena matrika tega sistema. Potem velja:
- sistem je rešljiv natanko tedaj, ko je
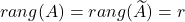 ;
; - sistem je enolično rešljiv natanko tedaj, ko je
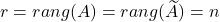 .
. - sistem ima neskončno rešitev natanko tedaj, ko je
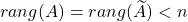 .
.
V zadnjem primeru lahko ![]() neznank poljubno izberemo kot parametre. Potem je
neznank poljubno izberemo kot parametre. Potem je ![]() neznank z njimi natanko določenih. Rečemo tudi, da ima sistem
neznank z njimi natanko določenih. Rečemo tudi, da ima sistem ![]() –parametrično rešitev.
–parametrično rešitev.
Primer 5.9: Rešite naslednji sistem:
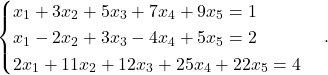
Preoblikujemo razširjeno matriko sistema v vrstično kanonično obliko:
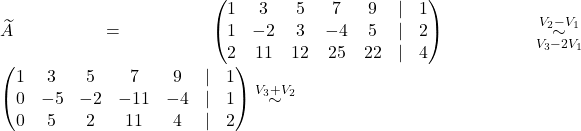
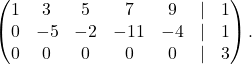
Torej, ![]() , kar pomeni, da je sistem nerešljiv.
, kar pomeni, da je sistem nerešljiv.
Izrek 5.3 [1,5]: Za kvadratno matriko ![]() reda
reda ![]() so naslednje trditve ekvivalentne:
so naslednje trditve ekvivalentne:
-
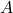 je obrnljiva matrika,
je obrnljiva matrika, -
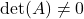 ,
, -
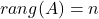 ,
, - sistem linearnih enačb
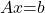 je enolično rešljiv za vsako desno stran
je enolično rešljiv za vsako desno stran  .
.
4. Homogeni sistemi
Homogeni sistem je poseben sistem linearnih enačb z ničelno desno stranjo: ![]() . Za tak sistem vedno velja
. Za tak sistem vedno velja ![]() torej je homogeni sistem vedno rešljiv in ima vedno rešitev
torej je homogeni sistem vedno rešljiv in ima vedno rešitev ![]() , ki se imenuje ničelna ali trivialna rešitev.
, ki se imenuje ničelna ali trivialna rešitev.
Če je ![]() , potem je rešitev ena sama (tj. ničelna rešitev), in če je
, potem je rešitev ena sama (tj. ničelna rešitev), in če je ![]() , ima homogeni sistem neskončno rešitev.
, ima homogeni sistem neskončno rešitev.
Primer 5.10: Rešimo naslednji homogeni sistem:

Ker je sistem homogen, je zadnji stolpec pri Gaussovi eliminacijski metodi v razširjeni matriki sistema vseskozi enak ![]() in ga zato kar izpustimo. Matriko sistema preoblikujemo v vrstično kanonično obliko:
in ga zato kar izpustimo. Matriko sistema preoblikujemo v vrstično kanonično obliko:
![]()
Opazimo, da je ![]() in rešitev je 1-parametrična, ker je
in rešitev je 1-parametrična, ker je ![]() . Pripadajoči sistem je
. Pripadajoči sistem je
![Rendered by QuickLaTeX.com \[\begin{cases} x + 2y-5z = 0 \\ y -4z = 0 \end{cases}. \end{equation*}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-f1648daffba9f929c4313925a9289406_l3.png)
Če kot parameter izberemo ![]() , dobimo
, dobimo ![]() in potem
in potem ![]()
Primer 5.11: Rešimo naslednji homogeni sistem:
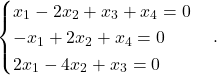
Matriko sistema preoblikujemo v vrstično kanonično obliko:
![Rendered by QuickLaTeX.com \[A =\begin{pmatrix} 1 & -2 & 1 & 1\\ -1 & 2 & 0 & 1 \\ 2 & -4 & 1 & 0 \end{pmatrix}\overset{V_2+ V_1}{\underset{V_3-2V_1}{\sim}} \begin{pmatrix} 1 & -2 & 1 & 1\\ 0 & 0 & 1 & 2 \\ 0 & 0 & -1 & -2 \end{pmatrix} \overset{V_3+ V_2}{\sim} \begin{pmatrix} 1 & -2 & 1 & 1\\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-1303622fde16f943ae6dbcfc9cb750bd_l3.png)
Torej, ![]() in rešitev ima parametra, ker je
in rešitev ima parametra, ker je ![]() . Pripadajoči sistem je
. Pripadajoči sistem je
![Rendered by QuickLaTeX.com \[\begin{cases} x_1 - 2x_2 + x_3 + x_4 = 0 \\ x_3 + 2x_4 = 0 \end{cases}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-26e2fff25133acc1a715291b7468e09f_l3.png)
Dobimo ![]() in
in ![]() , kjer sta
, kjer sta ![]() in
in ![]() poljubni realni števili.
poljubni realni števili.