7 Vektorji v prostoru
Poglavje obravnava geometrijske vektorje v prostoru ![]() .
.
- Definicija in osnove operacije
Definicija 7.1: Geometrijski vektor v ![]() je usmerjena daljica, ki je natanko določena s svojo začetno in končno točko
je usmerjena daljica, ki je natanko določena s svojo začetno in končno točko ![]() in
in ![]() . Označimo ga z
. Označimo ga z ![]() Dolžina vektorja ali absolutna vrednost ali norma vektorja (oznaka
Dolžina vektorja ali absolutna vrednost ali norma vektorja (oznaka ![]() ) je enaka razdalji med točkama
) je enaka razdalji med točkama ![]() in
in ![]() .
.
Dva vektorja sta enaka, če imata isto dolžino in isto smer.
1) Seštevanje vektorjev
Naj bosta ![]() in
in ![]() poljubna vektorja. Vektorja
poljubna vektorja. Vektorja ![]() in
in ![]() lahko premaknemo tako, da konec vektorja
lahko premaknemo tako, da konec vektorja ![]() sovpada z začetkom vektorja
sovpada z začetkom vektorja ![]() . Potem je vektor
. Potem je vektor ![]() usmerjena daljica od začetka vektorja
usmerjena daljica od začetka vektorja ![]() do konca vektorja
do konca vektorja ![]() . Ta metoda seštevanja je prikazana na sliki 7.1.
. Ta metoda seštevanja je prikazana na sliki 7.1.
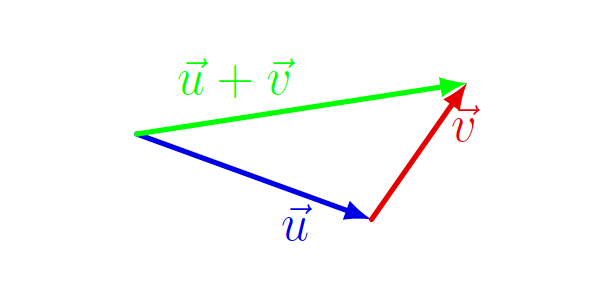
Če imata vektorja ![]() in
in ![]() skupno začetno točko, je njuna vsota
skupno začetno točko, je njuna vsota ![]() velika diagonala paralelograma, ki ima vektorja
velika diagonala paralelograma, ki ima vektorja ![]() in
in ![]() za stranici (glej sliko 7.2).
za stranici (glej sliko 7.2).
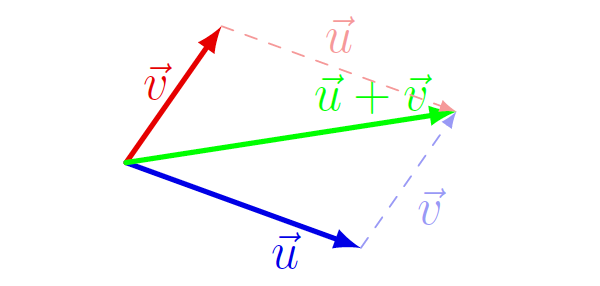
Vektor, ki se začne in konča v isti točki, imenujemo ničelni vektor ![]() . Velja:
. Velja:
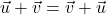 ;
;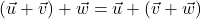 ;
;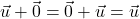 ;
;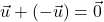 , kjer je
, kjer je 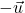 nasprotni vektor vektorja
nasprotni vektor vektorja 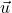 . To pomeni: če je
. To pomeni: če je 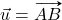 , potem je
, potem je 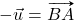 .
.
Vsak vektor lahko postavimo v prostoru ![]() tako, da je njegova začetna točka v izhodišču
tako, da je njegova začetna točka v izhodišču ![]() koordinatnega sistema. Tedaj je vektor enolično določen s svojo končno točko
koordinatnega sistema. Tedaj je vektor enolično določen s svojo končno točko ![]() in vektor
in vektor ![]() se imenuje krajevni vektor točke
se imenuje krajevni vektor točke ![]() . Vektor potem predstavimo kot urejeno trojico realnih števil, zapisano v obliki stolpca
. Vektor potem predstavimo kot urejeno trojico realnih števil, zapisano v obliki stolpca 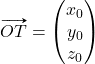 ali v obliki vrstice
ali v obliki vrstice ![]() . V nadaljevanju bomo uporabili samo drugi zapis.
. V nadaljevanju bomo uporabili samo drugi zapis.
Lahko pišemo torej ![]() in
in ![]() se imenujejo komponente vektorja
se imenujejo komponente vektorja ![]() .
.
Če obstajata poljubna vektorja ![]() in
in ![]() , potem velja:
, potem velja:
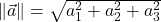 ;
;- nasprotni vektor je
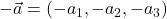 ;
; 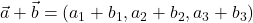 .
.
Primer 7.1: Naj bosta vektorja ![]() in
in ![]() .
.
Dobimo ![]() ,
, ![]() ter
ter ![]() .
.
2) Množenje vektorja s skalarjem
Naj bo ![]() poljubno realno število. Vektor
poljubno realno število. Vektor ![]() ima dolžino
ima dolžino ![]() in leži na isti premici, na kateri leži vektor
in leži na isti premici, na kateri leži vektor ![]() . Če je
. Če je ![]() , ima vektor
, ima vektor ![]() enako smer kot
enako smer kot ![]() . Če je
. Če je ![]() , potem ima vektor
, potem ima vektor ![]() enako smer kot
enako smer kot ![]() , in če je
, in če je ![]() , je
, je ![]() ničelni vektor.
ničelni vektor.
Lastnosti:
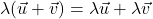 ;
;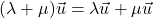 ;
;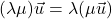 .
.
Za dani poljubni točki ![]() in
in ![]() zapišemo vektor
zapišemo vektor ![]() po komponentah kot
po komponentah kot ![]() .
.
2. Linearna kombinacija, neodvisnost in baza
Vsak vektor ![]() v
v ![]() se zapiše kot izraz
se zapiše kot izraz
![]()
kjer so ![]() enotski vektorji (saj je
enotski vektorji (saj je ![]() ). Zato rečemo, da se vsak vektor
). Zato rečemo, da se vsak vektor ![]() zapiše kot linearna kombinacija vektorjev
zapiše kot linearna kombinacija vektorjev ![]() oziroma
oziroma
![]()
Množica vektorjev ![]() se imenuje standardna baza vektorskega prostora
se imenuje standardna baza vektorskega prostora ![]() .
.
Definicija 7.2: Izraz ![]() imenujemo linearna kombinacija vektorjev
imenujemo linearna kombinacija vektorjev ![]() . Skalarji
. Skalarji ![]() se imenujejo koeficienti linearne kombinacije.
se imenujejo koeficienti linearne kombinacije.
Linearna kombinacija je trivialna, če je ![]() . Če je vsaj en
. Če je vsaj en ![]() , je linearna kombinacija vektorjev netrivialna.
, je linearna kombinacija vektorjev netrivialna.
Definicija 7.3: Vektorji ![]() so linearno neodvisni, če velja:
so linearno neodvisni, če velja:
![]()
Sicer pa so linearno odvisni.
Opomba 7.1:
Vektorji ![]() so linearno odvisni, če je eden od njih linearna kombinacija drugih. Prav zares, obstajajo skalarji
so linearno odvisni, če je eden od njih linearna kombinacija drugih. Prav zares, obstajajo skalarji ![]() (niso vsi enaki nič, torej lahko domnevamo, da je
(niso vsi enaki nič, torej lahko domnevamo, da je ![]() ) tako, da je
) tako, da je ![]() . Sledi, da je
. Sledi, da je
![]()
Opomba 7.2:
Dva vektorja ![]() in
in ![]() sta linearno odvisna, če je
sta linearno odvisna, če je ![]() z
z ![]() . V tem primeru
. V tem primeru ![]() in
in ![]() ležita na isti premici in pravimo, da sta kolinearna.
ležita na isti premici in pravimo, da sta kolinearna.
Trije vektorji ![]() in
in ![]() so linearno odvisni, če obstajata
so linearno odvisni, če obstajata ![]() tako, da je
tako, da je ![]() . V tem primeru trije vektorji ležijo na isti ravnini in so komplanarni.
. V tem primeru trije vektorji ležijo na isti ravnini in so komplanarni.
Primer 7.2: Naj bosta dana vektorja ![]() in
in ![]() . Ker je
. Ker je ![]() , sta dana vektorja linearno odvisna in tudi kolinearna.
, sta dana vektorja linearno odvisna in tudi kolinearna.
Primer 7.3: Zapišimo vektor ![]() kot linearno kombinacijo vektorjev
kot linearno kombinacijo vektorjev ![]() ,
, ![]() in
in ![]() .
.
Vektor ![]() se izraža kot linearna kombinacija vektorjev
se izraža kot linearna kombinacija vektorjev ![]() ter
ter ![]() , če obstajajo skalarni
, če obstajajo skalarni ![]() tako, da je
tako, da je ![]() .
.
To je ekvivalentno z
![]()
Dobimo sistem
![Rendered by QuickLaTeX.com \[\begin{cases} \alpha+3\beta+\gamma=8\\ -2\alpha+2\beta=6\\ \alpha+\beta-\gamma=4\end{cases},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4f66060947fe8b10f61be9ce202087c1_l3.png)
ki ga rešujemo po Gaussovi eliminacijski metodi. Razširjeno matriko sistema preoblikujemo v vrstično kanonično obliko
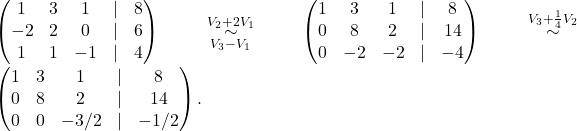
Pripadajoči sistem je
![Rendered by QuickLaTeX.com \[\begin{cases} \alpha+3\beta+\gamma=8\\ 8\beta+2\gamma=14\\ 3\gamma=1\end{cases},\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-0f1d3977d14af88df1b1d586c3344f6f_l3.png)
ki ima rešitev ![]() ,
, ![]() in
in ![]() . Torej se vektor
. Torej se vektor ![]() izraža kot
izraža kot ![]() .
.
3. Skalarni, vektorski in mešani produkt
1) Skalarni produkt vektorjev
Definicija 7.4: Skalarni produkt vektorjev ![]() in
in ![]() je število
je število ![]() (beremo
(beremo ![]() skalarno
skalarno ![]() ).
).
Primer 7.4: Za vektorja ![]() in
in ![]() izračunajmo produkta.
izračunajmo produkta. ![]() in
in ![]() .
.
Lastnosti skalarnega produkta. Za poljubne vektorje ![]() ,
, ![]() in
in ![]() , velja [1]:
, velja [1]:
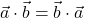 (simetričnost);
(simetričnost);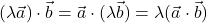 , za vse
, za vse 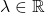 (homogenost);
(homogenost);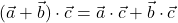 (aditivnost);
(aditivnost);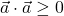 in
in 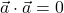 natanko tedaj, ko je
natanko tedaj, ko je 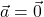 (pozitivna definitnost).
(pozitivna definitnost).
Geometrijski pomen skalarnega produkta.
Norma vektorja ![]() je definirana s predpisom
je definirana s predpisom ![]() .
.
Če je ![]() kot med vektorjema
kot med vektorjema ![]() in
in ![]() , potem je
, potem je
![Rendered by QuickLaTeX.com \[\cos\varphi=\displaystyle\frac{\vec{a}\cdot \vec{b}}{\norm{\vec{a}}\norm{\vec{b}}}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-08a7e295bf2971d40b7dfb8bde5e47b8_l3.png)
Sledi, da sta vektorja ![]() in
in ![]() med seboj pravokotna natanko tedaj, ko je
med seboj pravokotna natanko tedaj, ko je ![]() Ničelni vektor
Ničelni vektor ![]() je pravokoten na vsak drug vektor.
je pravokoten na vsak drug vektor.
Standardni bazni vektorji ![]() v
v ![]() so enotski in paroma pravokotni, tj.
so enotski in paroma pravokotni, tj. ![]() in
in ![]() .
.
Primer 7.5: Poiščimo kot med vektorjema ![]() in
in ![]() . Ali sta linearno odvisna? Ali sta pravokotna?
. Ali sta linearno odvisna? Ali sta pravokotna?
Izračunamo skalarni produkt vektorjev ![]() in
in ![]() :
: ![]() . To pomeni, da vektorja
. To pomeni, da vektorja ![]() in
in ![]() nista pravokotna. Če je
nista pravokotna. Če je ![]() kot med
kot med ![]() in
in ![]() , je
, je
![Rendered by QuickLaTeX.com \[\cos\varphi=\displaystyle\frac{\vec{a}\cdot \vec{b}}{\norm{\vec{a}}\cdot\norm{\vec{b}}}=\frac{-10}{3\cdot 5}=-\frac{2}{3}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-b5c96bb4793c98b4f8191133f0a6560b_l3.png)
Vektorja ![]() in
in ![]() sta linearno odvisna, če obstaja neki
sta linearno odvisna, če obstaja neki ![]() tako, da je
tako, da je ![]() oziroma
oziroma 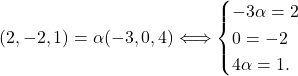 Ker je sistem nerešljiv, sledi, da sta vektorja
Ker je sistem nerešljiv, sledi, da sta vektorja ![]() in
in ![]() linearno neodvisna.
linearno neodvisna.
2) Vektorski produkt vektorjev
Definicija 7.5: Vektorski produkt vektorjev ![]() in
in ![]() je vektor
je vektor ![]() (beremo
(beremo ![]() vektorsko
vektorsko ![]() ), za katerega velja:
), za katerega velja:
- vektor
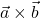 je pravokoten na vektorja
je pravokoten na vektorja 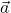 in
in 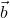 ;
; - ima dolžino
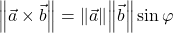 , kjer je
, kjer je 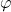 kot med vektorjema
kot med vektorjema 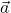 in
in 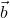 ;
; - če
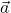 po krajši poti zavrtimo do
po krajši poti zavrtimo do 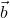 , ima vektor
, ima vektor 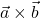 smer desnega vijaka.
smer desnega vijaka.
Lastnosti vektorskega produkta. Za poljubne vektorje ![]() ,
, ![]() in
in ![]() , velja [1]:
, velja [1]:
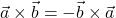 (antikomutativnost);
(antikomutativnost);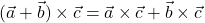 in
in 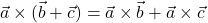 (aditivnost);
(aditivnost);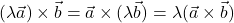 , za poljubno realno število
, za poljubno realno število 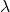 (homogenost);
(homogenost);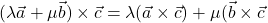 ), za poljubni realni števili
), za poljubni realni števili 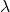 in
in 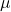 (linearnost);
(linearnost);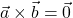 natanko tedaj, ko sta vektorja
natanko tedaj, ko sta vektorja 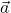 in
in 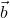 kolinearna, torej linearno odvisna; posebej velja
kolinearna, torej linearno odvisna; posebej velja 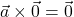 in
in 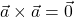 ;
;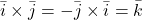 ;
; 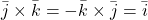 ;
; 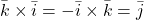 ;
;- za vektorja
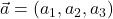 in
in 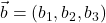 z razvojem determinante po prvi vrstici izračunamo
z razvojem determinante po prvi vrstici izračunamo
![Rendered by QuickLaTeX.com \[\vec{a}\times \vec{b}=\begin{vmatrix} \bar{i}& \bar{j} & \bar{k}\\ a_1 & a_2 &a_3\\ b_1 & b_2 & b_3\end{vmatrix}=(a_2b_3-a_3b_2, a_1b_3-a_3b_1, a_1b_2-a_2b_1).\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-ac7b7631c55e935ff2e6ee1105ddb995_l3.png)
Geometrijski pomen vektorskega produkta.
Dolžina vektorskega produkta ![]() je enaka ploščini paralelograma, ki ga določata vektorja
je enaka ploščini paralelograma, ki ga določata vektorja ![]() in
in ![]() , kar je
, kar je ![]() , kjer je
, kjer je ![]() kot med vektorjema
kot med vektorjema ![]() in
in ![]() .
.
Primer 7.6: Izračunajmo vektorski produkt vektorjev ![]() in
in ![]() .
.
Z razvojem determinante po prvi vrstici izračunamo
![Rendered by QuickLaTeX.com \[\vec{a}\times \vec{b}=\begin{vmatrix} \bar{i}& \bar{j} & \bar{k}\\ 1 & 2 &3\\ -1 & 0 & 2\end{vmatrix}=(4, -5, 2).\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-5c717f4bf9214e7e387626fbf994fab2_l3.png)
Primer 7.7: Določimo ploščino trikotnika z oglišči v točkah ![]() ,
, ![]() in
in ![]() .
.
Trikotnik ![]() je napet na vektorja
je napet na vektorja ![]() in
in ![]() .
.
Ploščina trikotnika ![]() je enaka polovici ploščine paralelograma, napetega na vektorja
je enaka polovici ploščine paralelograma, napetega na vektorja ![]() in
in ![]() , torej je
, torej je
![]() . Računamo
. Računamo 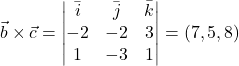 . Sledi, da je
. Sledi, da je ![]() .
.
Primer 7.8: Vektorja ![]() in
in ![]() oklepata kot
oklepata kot ![]() . Izračunajte ploščino paralelograma, napetega na vektorja
. Izračunajte ploščino paralelograma, napetega na vektorja ![]() in
in ![]() , če je
, če je ![]() in
in ![]() .
.
Označimo s ![]() kot med vektorjema
kot med vektorjema ![]() in
in ![]() , tj.
, tj. ![]() . Ploščina paralelograma, napetega na vektorja
. Ploščina paralelograma, napetega na vektorja ![]() in
in ![]() , je enaka normi vektorskega produkta
, je enaka normi vektorskega produkta ![]() , ker je
, ker je ![]() in
in ![]() . To pomeni, da je ploščina iskanega paralelograma enaka
. To pomeni, da je ploščina iskanega paralelograma enaka
![]()
3) Mešani produkt vektorjev
Definicija 7.6: Mešani produkt vektorjev ![]() ,
, ![]() in
in ![]() je število
je število
![Rendered by QuickLaTeX.com \[(\vec{a}, \vec{b}, \vec{c})=(\vec{a}\times \vec{b})\cdot \vec{c}=\begin{vmatrix}a_1&a_2&a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3\end{vmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-756272effbe0e781b2a8bd431ff0a432_l3.png)
Geometrijski pomen mešanega produkta
Absolutna vrednost mešanega produkta ![]() je enaka prostornini (ali volumnu) paralelepipeda, napetega na vektorje
je enaka prostornini (ali volumnu) paralelepipeda, napetega na vektorje ![]() ,
, ![]() in
in ![]() .
.
Sledi, da je ![]() natanko tedaj, ko so vektorji
natanko tedaj, ko so vektorji ![]() ,
, ![]() in
in ![]() komplanarni.
komplanarni.
Primer 7.9: Določimo vrednost parametra ![]() tako, da bodo vektorji
tako, da bodo vektorji ![]() ,
, ![]() ter
ter ![]() komplanarni.
komplanarni.
Vektorji ![]() so komplanarni, ko je vrednost njihovega mešanega produkta enaka
so komplanarni, ko je vrednost njihovega mešanega produkta enaka ![]() , torej ko je
, torej ko je
![Rendered by QuickLaTeX.com \[\begin{vmatrix} -1&1&2\\ \lambda& 0& 1\\ 1&2&-1\end{vmatrix}=5\lambda+3=0.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-6df8c981a9a0255b786248e2098b5f82_l3.png)
Iz tega izhaja, da je ![]()
4. Enačba ravnine v prostoru
Ravnina v trirazsežnem prostoru je določena na dva načina.
- S točko
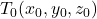 na ravnini in njeno pravokotnico (normalo) oziroma normalnim vektorjem
na ravnini in njeno pravokotnico (normalo) oziroma normalnim vektorjem 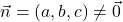 (glej sliko 7.3).
(glej sliko 7.3).
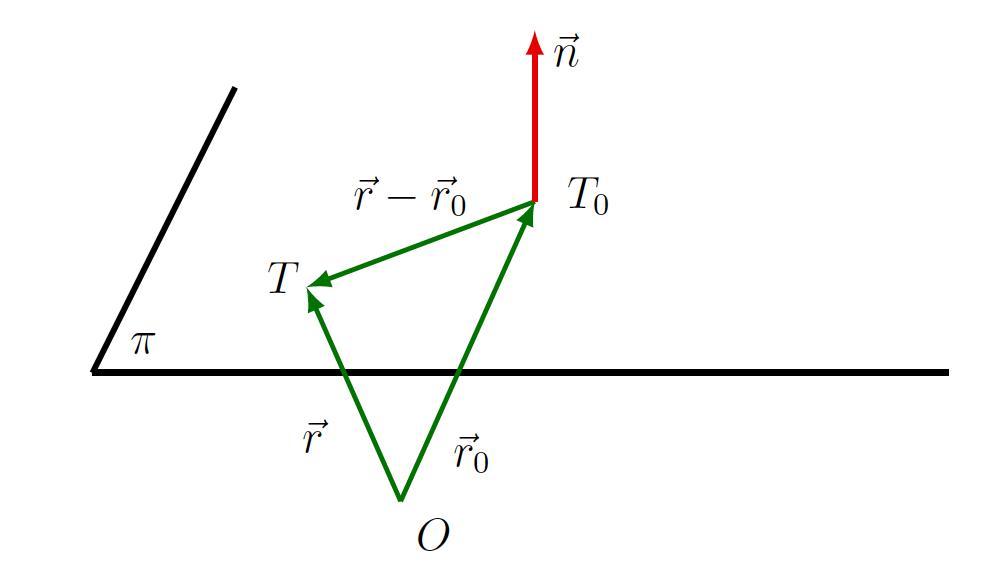
 s pravokotnico
s pravokotnico 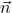 .
.Poiskati enačbo ravnine ![]() v prostoru pomeni poiskati neko zvezo med danimi podatki (tj. točko
v prostoru pomeni poiskati neko zvezo med danimi podatki (tj. točko ![]() in normalnim vektorjem
in normalnim vektorjem ![]() ) in koordinatami poljubne točke
) in koordinatami poljubne točke ![]() na ravnini. Ker leži vektor
na ravnini. Ker leži vektor ![]() na ravnini
na ravnini ![]() , je pravokoten na normalni vektor
, je pravokoten na normalni vektor ![]() , to pomeni, da velja
, to pomeni, da velja
(1) ![]()
kar je vektorska oblika enačbe ravnine.
V to enačbo vstavimo koordinate in dobimo splošno obliko enačbe ravnine:
![]()
![]()
oziroma
(2) ![]()
- S tremi točkami
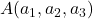 ,
, 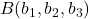 in
in 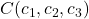 na ravnini, ki ne ležijo na isti premici (glej sliko 7.4).
na ravnini, ki ne ležijo na isti premici (glej sliko 7.4).
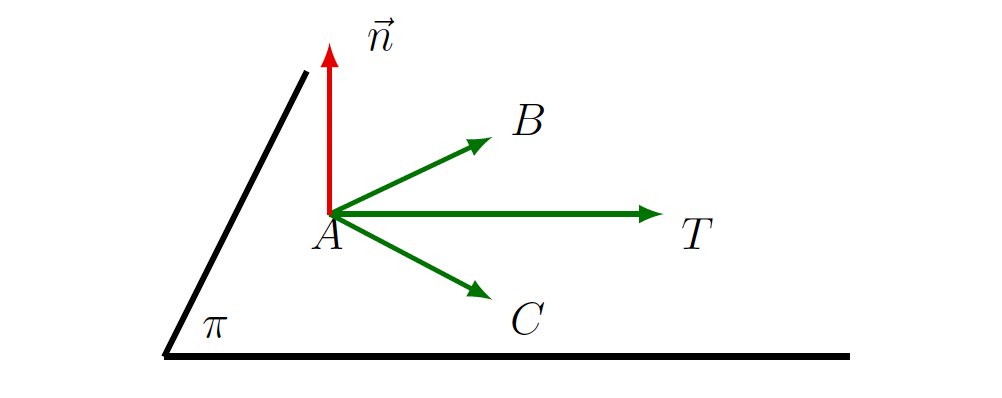
 s tremi točkami
s tremi točkami 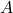 ,
, 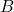 in
in 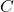 .
.V tem primeru izračunamo normalni vektor ravnine kot vektorski produkt ![]() . Poleg tega velja: če je
. Poleg tega velja: če je ![]() poljubna točka na ravnini
poljubna točka na ravnini ![]() , potem so vektorji
, potem so vektorji ![]() ,
, ![]() in
in ![]() komplanarni, torej je njihov mešani produkt
komplanarni, torej je njihov mešani produkt ![]() :
:
(3) 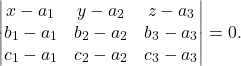
Vektorji ![]() ,
, ![]() in
in ![]() so linearno odvisni, torej dobimo parametrično obliko enačbe ravnine
so linearno odvisni, torej dobimo parametrično obliko enačbe ravnine
![]()
oziroma
(4) ![]()
Primer 7.10: Zapišimo enačbo ravnine, ki gre skozi točke ![]() ,
, ![]() in
in ![]() .
.
Uporabimo enačbo (3) in dobimo
![Rendered by QuickLaTeX.com \[\begin{vmatrix} x-4& y-3& z-0\\ 4-4& 0-3& -1-0\\ 0-4& 3-3& 2-0 \end{vmatrix}=0\Longleftrightarrow \begin{vmatrix} x-4& y-3& z\\ 0& -3& -1\\ -4& 0& 2 \end{vmatrix}=0.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-f15269d8fb5bd5e2e92065b755de7d34_l3.png)
Z razvojem determinanta po prvi vrstici dobimo enčbo iskane ravnine:
![]()
5. Enačba premice v prostoru
Premica ![]() v prostoru
v prostoru ![]() je določena različno.
je določena različno.
- S točko
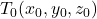 na premici in smernim vektorjem
na premici in smernim vektorjem 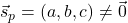 (glej sliko 7.5).
(glej sliko 7.5).
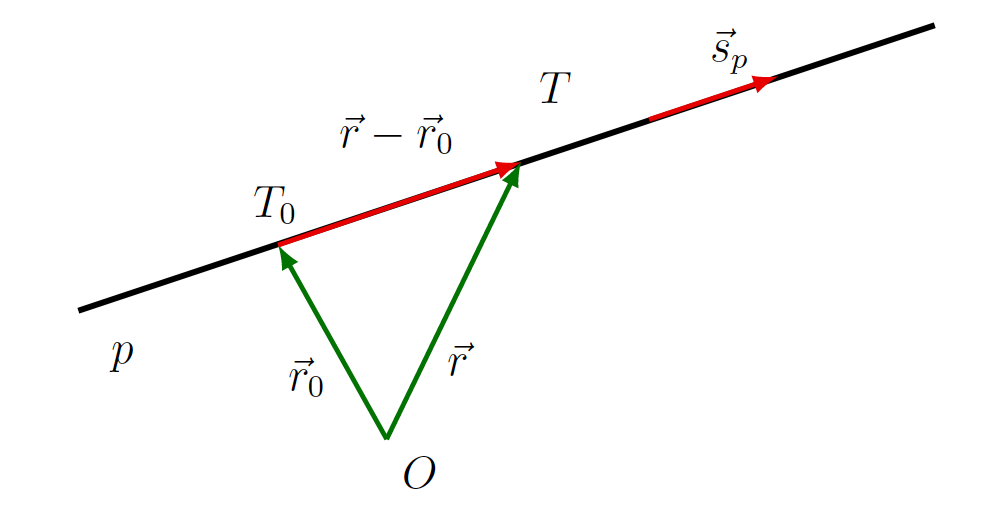
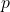 skozi točko
skozi točko 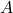 s smernim vektorjem
s smernim vektorjem  .
.Ker sta vektorja ![]() in
in ![]() kolinearna (torej tudi linearno odvisna), lahko zapišemo relacijo
kolinearna (torej tudi linearno odvisna), lahko zapišemo relacijo ![]() , kjer je
, kjer je ![]() poljubno realno število. Tako dobimo vektorsko obliko enačbe premice:
poljubno realno število. Tako dobimo vektorsko obliko enačbe premice:
(5) ![]()
Če v to formulo vstavimo koordinate ![]() ,
, ![]() in
in ![]() , dobimo parametrično obliko enačbe premice:
, dobimo parametrično obliko enačbe premice:
(6) 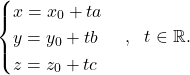
Če izrazimo parameter ![]() , dobimo kanonično obliko enačbe premice:
, dobimo kanonično obliko enačbe premice:
(7) ![]()
- Z dvema različnima točkama
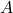 in
in 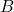 . V tem primeru smerni vektor premice
. V tem primeru smerni vektor premice 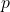 bo
bo 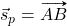 (glej sliko 7.6).
(glej sliko 7.6).
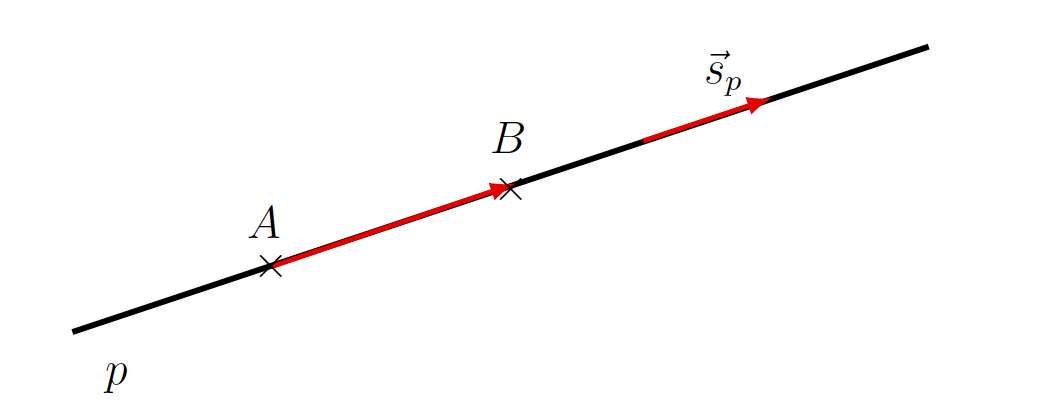
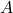 in
in 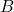 .
.- Z dvema nevzporednima ravninama
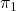 in
in 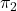 oziroma kot presek ravnin:
oziroma kot presek ravnin:
(8)
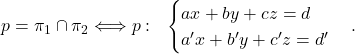
6. Razdalja med točko in ravnino
Ravnina ![]() naj bo določena z normalnim vektorjem
naj bo določena z normalnim vektorjem ![]() in točko
in točko ![]() (ali s krajevnim vektorjem
(ali s krajevnim vektorjem ![]() ). Oddaljenost točke
). Oddaljenost točke ![]() od ravnine
od ravnine ![]()
![]() je najkrajša razdalja med dano točko in poljubno točko
je najkrajša razdalja med dano točko in poljubno točko ![]() na ravnini (glej sliko 7.7).
na ravnini (glej sliko 7.7).
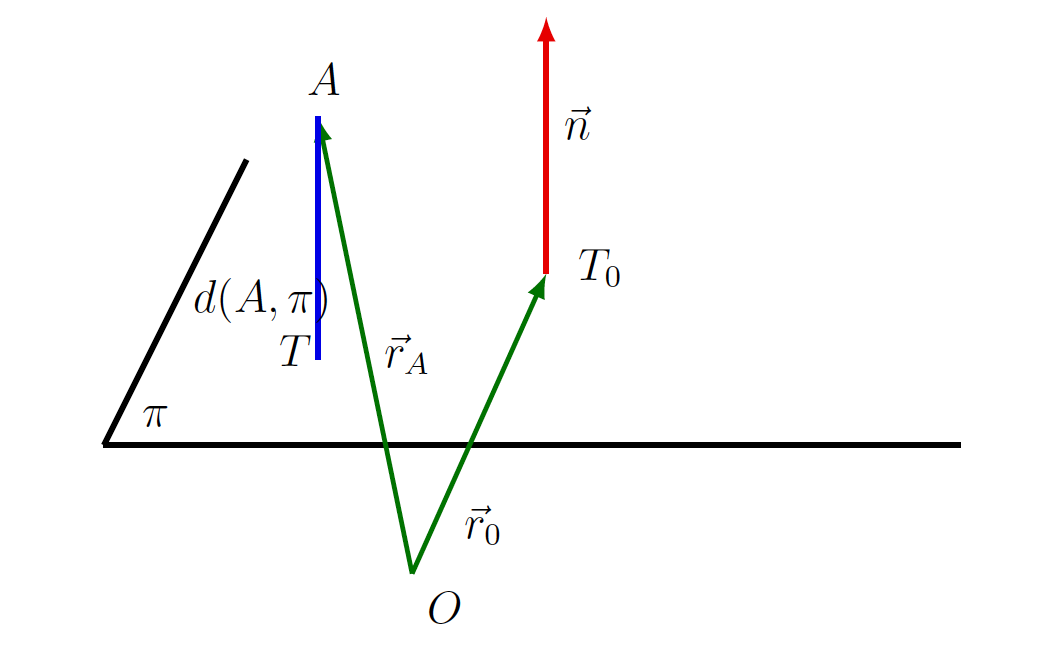
Razdalja ![]() je enaka dolžini projekcije vektorja
je enaka dolžini projekcije vektorja ![]() na normalni vektor
na normalni vektor ![]() ravnine
ravnine ![]() , podane z enačbo
, podane z enačbo ![]() , torej je
, torej je
(9) ![]()
Primer 7.11: Izračunajmo razdaljo med točko ![]() in ravnino
in ravnino ![]() .
.
Normalni vektor ravnine ![]() je
je ![]() , koeficient
, koeficient ![]() ter koordinate točke
ter koordinate točke ![]() so
so ![]() . Dobimo, da je razdalja med točko
. Dobimo, da je razdalja med točko ![]() in ravnino
in ravnino ![]() enaka
enaka
![]()
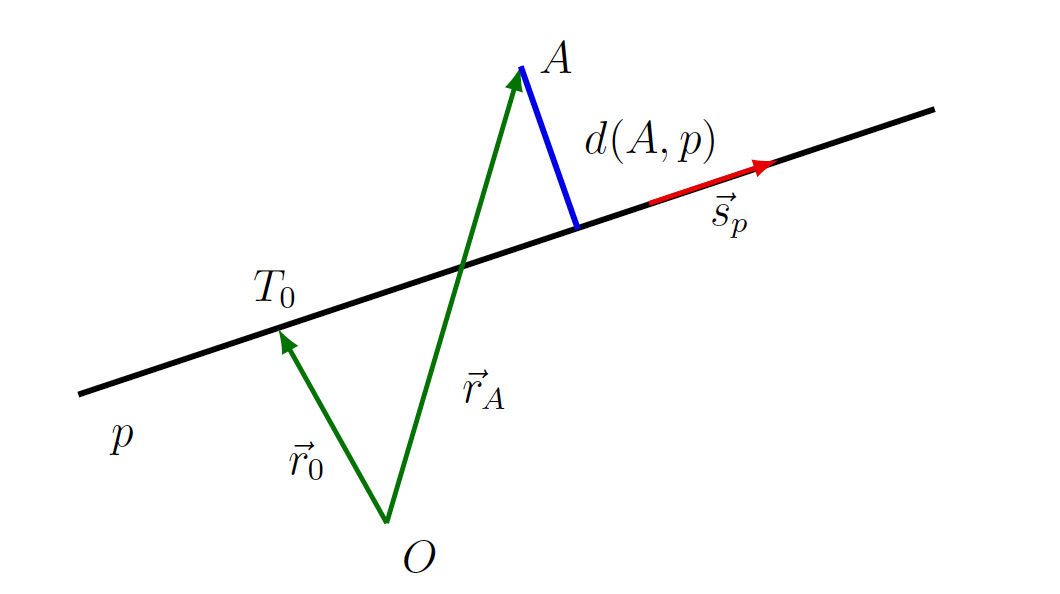
7. Razdalja med točko in premico
Premica ![]() naj bo določena s točko
naj bo določena s točko ![]() (ali s krajevnim vektorjem
(ali s krajevnim vektorjem ![]() ) in smernim vektorjem
) in smernim vektorjem ![]() in naj bo
in naj bo ![]() poljubna točka (glej sliko 7.8).
poljubna točka (glej sliko 7.8).
 in premico
in premico 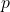 .
.Razdalja med točko in premico ![]() je najmanjša razdalja med točko
je najmanjša razdalja med točko ![]() in neko točko na premici, torej je
in neko točko na premici, torej je
(10) ![]()
Primer 7.12: Izračunajmo razdaljo med točko ![]() in premico
in premico ![]()
Če točka pripada premici, je razdalja med njima enaka ![]() . Torej, najprej preverimo, ali je dana točka
. Torej, najprej preverimo, ali je dana točka ![]() na premici
na premici ![]() . V tem primeru ni tako, saj koordinate točke ne zadoščajo enačbi premice:
. V tem primeru ni tako, saj koordinate točke ne zadoščajo enačbi premice: ![]() . Krajevni vektor točke
. Krajevni vektor točke ![]() je
je ![]() , smerni vektor premice
, smerni vektor premice ![]() je
je ![]() ter krajevni vektor točke na premici
ter krajevni vektor točke na premici ![]() . Izračunamo vektorski produkt
. Izračunamo vektorski produkt
![Rendered by QuickLaTeX.com \[(\vec{r}_A-\vec{r}_0)\times \vec{s}_p=(-1,1,0)\times (1,2,3)=\begin{vmatrix} \bar{i}&\bar{j}&\bar{k}\\-1&1&0\\ 1&2&3\end{vmatrix}=(3,3,-3).\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-de70535b8d942e00929c4b2c9bec35ed_l3.png)
Po formuli (10) sledi, da je razdalja med točko ![]() in premico
in premico ![]() enaka
enaka
![]()
