1 Matrike
- Osnovni pojmi in lastnosti matrik
Definicija 1.1: Matrika velikosti ![]() je tabela realnih (ali kompleksnih) števil, ki se imenujejo členi ali elementi matrike, z
je tabela realnih (ali kompleksnih) števil, ki se imenujejo členi ali elementi matrike, z ![]() vrsticami in
vrsticami in ![]() stolpci. Število vrstic in število stolpcev določata red matrike, to je torej
stolpci. Število vrstic in število stolpcev določata red matrike, to je torej ![]() . Matrike označujemo z velikimi črkami:
. Matrike označujemo z velikimi črkami:

Na kratko bomo zapisali ![]() . Element matrike
. Element matrike ![]() , ki leži v
, ki leži v ![]() -ti vrstici in
-ti vrstici in ![]() -tem stolpcu, označimo z
-tem stolpcu, označimo z ![]() . Množico vseh matrik realnih števil z
. Množico vseh matrik realnih števil z ![]() vrsticami in
vrsticami in ![]() stolpci označimo z
stolpci označimo z ![]() ali
ali ![]() .
.
Vrstica je matrika reda ![]() , na primer
, na primer ![]() , medtem ko je stolpec matrika reda
, medtem ko je stolpec matrika reda ![]() ,
, 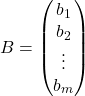 . Če je
. Če je ![]() , matriko imenujemo kvadratna, saj ima enako število vrstic in stolpcev.
, matriko imenujemo kvadratna, saj ima enako število vrstic in stolpcev.
Ničelna matrika ![]() je matrika, katere členi so vsi enaki
je matrika, katere členi so vsi enaki ![]() . Identična (enotska) matrika reda
. Identična (enotska) matrika reda ![]() (ali reda
(ali reda ![]() ) je kvadratna matrika, ki ima po diagonali enice, drugod pa ničle. Na primer, identična matrika reda
) je kvadratna matrika, ki ima po diagonali enice, drugod pa ničle. Na primer, identična matrika reda ![]() je matrika
je matrika
![Rendered by QuickLaTeX.com \[I_4= \begin{pmatrix} 1 & 0 & 0 & 0\\ 0& 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-0dc42fa1b881fa232736b4a4903de0ab_l3.png)
Matriki ![]() in
in ![]() sta enaki, če sta istega reda in imata enake člene:
sta enaki, če sta istega reda in imata enake člene: ![]() , za vsak
, za vsak ![]() ,
, ![]() in
in ![]() .
.
2. Računske operacije z matrikami
Seštevanje matrik
Naj bosta ![]() in
in ![]() matriki istega reda
matriki istega reda ![]() . Če ju seštejemo, dobimo novo matriko
. Če ju seštejemo, dobimo novo matriko ![]() , kjer je
, kjer je ![]() . Vsoto matrik dobimo tako, da seštejemo istoležne elemente matrik. Rezultat je istega reda kot matriki, ki ju seštevamo.
. Vsoto matrik dobimo tako, da seštejemo istoležne elemente matrik. Rezultat je istega reda kot matriki, ki ju seštevamo.
Primer 1.1: Izračunajmo vsoto matrik ![]() in
in ![]() . Po definiciji dobimo
. Po definiciji dobimo
![]()
-
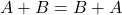 (komutativnost);
(komutativnost); -
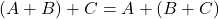 (asociativnost);
(asociativnost); -
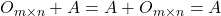 , kjer je
, kjer je 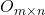 ničelna matrika reda
ničelna matrika reda 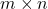 , ki se imenuje enota za seštevanje;
, ki se imenuje enota za seštevanje; - za vsako matriko
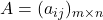 obstaja matrika
obstaja matrika 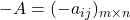 , tako da je
, tako da je 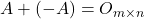 ; matrika
; matrika 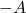 se imenuje inverz za seštevanje.
se imenuje inverz za seštevanje.
Produkt matrik s skalarjem
Produkt matrike ![]() s skalarjem
s skalarjem ![]() je matrika
je matrika
![Rendered by QuickLaTeX.com \[\alpha\cdot A=(\alpha \cdot (a_{ij}))_{m\times n} = \begin{pmatrix} \alpha\cdot a_{11} & \alpha\cdot a_{12} & \ldots & \alpha\cdot a_{1n}\\ \alpha\cdot a_{21} & \alpha\cdot a_{22} & \ldots & \alpha\cdot a_{2n}\\ \vdots & \vdots & \ldots & \vdots\\ \alpha\cdot a_{m1} & \alpha\cdot a_{m2} & \ldots & \alpha\cdot a_{mn} \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-1dd75cdcb4ed44ed5b8ed68817fa7403_l3.png)
Vsak člen matrike ![]() pomnožimo s številom
pomnožimo s številom ![]() . Če je
. Če je ![]() , pišemo
, pišemo ![]() in zato lahko tudi razliko dveh matrik definiramo kot
in zato lahko tudi razliko dveh matrik definiramo kot ![]() .
.
Lastnosti množenja s skalarjem: Naj bosta ![]() in
in ![]() matriki istega reda ter
matriki istega reda ter ![]() in
in ![]() poljubna skalarja. Velja:
poljubna skalarja. Velja:
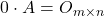 ;
; 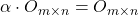 ;
;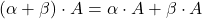 (distributivnost);
(distributivnost);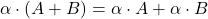 (distributivnost);
(distributivnost);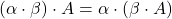 ;
;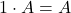 .
.
Transponiranje
Naj bo dana matrika ![]() . Definiramo novo matriko
. Definiramo novo matriko ![]() , ki se imenuje transponiranka matrike
, ki se imenuje transponiranka matrike ![]() ali transponirana matrika matrike
ali transponirana matrika matrike ![]() . Torej jo dobimo tako, da
. Torej jo dobimo tako, da ![]() -ta vrstica matrike
-ta vrstica matrike ![]() postane
postane ![]() -ti stolpec matrike
-ti stolpec matrike ![]() oziroma da zamenjamo istoležne vrstice in stolpce.
oziroma da zamenjamo istoležne vrstice in stolpce.
Primer 1.2: Naj bo ![]() in
in 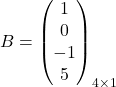 .
.
S transponiranjem dobimo 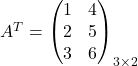 in
in ![]()
Lastnosti transponiranja: Naj bosta ![]() in
in ![]() matriki istega reda ter
matriki istega reda ter ![]() skalar. Velja:
skalar. Velja:
-
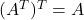 ;
; -
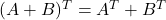 ;
; -
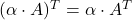 .
.
Kvadratna matrika ![]() se imenuje simetrična matrika, če velja
se imenuje simetrična matrika, če velja ![]() . Ko je
. Ko je ![]() , rečemo, da je
, rečemo, da je ![]() poševno simetrična matrika. Trivialen primer simetrične matrike je identična matrika, medtem ko je netrivialen primer naslednja matrika:
poševno simetrična matrika. Trivialen primer simetrične matrike je identična matrika, medtem ko je netrivialen primer naslednja matrika:
![Rendered by QuickLaTeX.com \[A=\begin{pmatrix} 2 & 0 & 3\\ 0 & -2 & 5\\ 3 & 5 & 6 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-bc2e0ee319fe25db7656ec2ac943bc55_l3.png)
Elementi na diagonali poševno simetrične matrike so vsi enaki nič.
Na primer, matrika 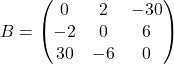 je poševno simetrična.
je poševno simetrična.
Množenje matrik
![Rendered by QuickLaTeX.com \[A\cdot B=C=(c_{ik})_{m\times p}, ~~c_{ik}=\displaystyle\sum_{j=1}^n a_{ij}\cdot b_{jk}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-7f5fd9366f020df8819cf227cf85e960_l3.png)
Matriki ![]() in
in ![]() pomnožimo tako, da pomnožimo
pomnožimo tako, da pomnožimo ![]() -to vrstico matrike
-to vrstico matrike ![]() z
z ![]() -tim stolpcem matrike
-tim stolpcem matrike ![]() ter produkte posameznih parov seštejemo. Rezultat, tj. matrika
ter produkte posameznih parov seštejemo. Rezultat, tj. matrika ![]() , ima toliko vrstic
, ima toliko vrstic ![]() kot prva matrika
kot prva matrika ![]() in toliko stolpcev
in toliko stolpcev ![]() kot druga matrika
kot druga matrika ![]() .
.
Primer 1.3: Naj bo 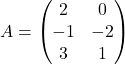 in
in ![]() .
.
Ker ima matrika ![]() dva stolpca, matrika
dva stolpca, matrika ![]() pa dve vrstici, lahko obe matriki pomnožimo in dobimo:
pa dve vrstici, lahko obe matriki pomnožimo in dobimo:
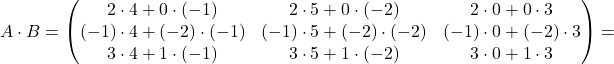
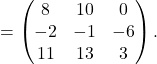
Ker je število stolpcev matrike ![]() enako številu vrstic matrike
enako številu vrstic matrike ![]() , lahko izračunamo tudi produkt
, lahko izračunamo tudi produkt ![]() . Dobimo
. Dobimo
![]()
![]()
Produkta ![]() ne moremo izračunati, ker ima matrika
ne moremo izračunati, ker ima matrika ![]() tri vrstice in samo dva stolpca.
tri vrstice in samo dva stolpca.
Primer 1.4: Izračunajmo produkt matrik ![]() in
in 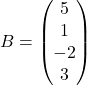 .
.
Dobimo
![Rendered by QuickLaTeX.com \[A\cdot B=\begin{pmatrix} 1 & 2 & 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 5 \\ 1 \\ -2\\ 3 \end{pmatrix} = 13.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-bcb7fa0caac19f79e8dd8810a28e17f8_l3.png)
Po množenju matrik ![]() in
in ![]() pa dobimo
pa dobimo
![Rendered by QuickLaTeX.com \[B\cdot A= \begin{pmatrix} 5 \\ 1 \\ -2\\ 3 \end{pmatrix}\cdot \begin{pmatrix} 1 & 2 & 3 & 4 \end{pmatrix} =\begin{pmatrix} 5 & 10 & 15 & 20\\ 1& 2& 3 & 4\\ -2 & -4 & -6 & -8\\ 3 & 6 & 9 & 12 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-53372beff735a4f571fac812376b63d4_l3.png)
To kaže, da če sta ![]() in
in ![]() oba definirana, potem ni nujno, da sta enaka ali da sta istega reda.
oba definirana, potem ni nujno, da sta enaka ali da sta istega reda.
Primer 1.5: Rešimo matrično enačbo nad ![]() :
:
![]()
Najprej opazimo, da je matrika ![]() reda
reda ![]() . Enačbo uredimo tako, da neznanko
. Enačbo uredimo tako, da neznanko ![]() prenesemo na levo stran:
prenesemo na levo stran:
![]()
Iz tega sledi, da je rešitev matrika ![]()
Lastnosti množenja matrik: Naj bodo dane matrike ![]() in
in ![]() ter skalar
ter skalar ![]() . Potem velja:
. Potem velja:
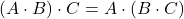 (asociativnost).
(asociativnost).- V splošnem produkt
 ni enak produktu
ni enak produktu 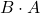 , tudi če oba produkta obstajata, torej množenje matrik ni komutativno.
, tudi če oba produkta obstajata, torej množenje matrik ni komutativno.
Na primer, če je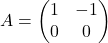 in
in 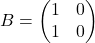 , dobimo, da je produkt
, dobimo, da je produkt 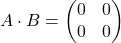 ter
ter 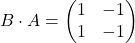 .
.
Poleg tega pri tem primeru opazimo tudi novo lastnost množenja matrik, in to je, da lahko dobimo ničelno matriko, če pomnožimo dve neničelni matriki. 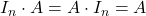 (identična matrika
(identična matrika 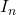 je enota za množenje matrik).
je enota za množenje matrik).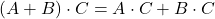 (distributivnost).
(distributivnost).-
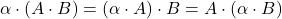 .
. 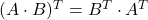 .
.
Primer 1.6: Če sta dani matriki 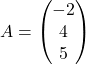 in
in ![]() , preverimo, da velja
, preverimo, da velja ![]() .
.
Najprej izračunamo produkt matrik in dobimo
![Rendered by QuickLaTeX.com \[A\cdot B= \begin{pmatrix} -2\\ 4 \\ 5 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3 & -6 \end{pmatrix} = \begin{pmatrix} -2 & -6 & 12\\ 4 & 12 & -24\\ 5 & 15 & -30 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-a077f03a07f69a6041a89895d1d38f2a_l3.png)
Potem, pri izračunu produkta transponirank, dobimo
![Rendered by QuickLaTeX.com \[B^T\cdot A^T = \begin{pmatrix} 1\\ 3\\ -6 \end{pmatrix} \cdot \begin{pmatrix} -2 & 4 & 5 \end{pmatrix} = \begin{pmatrix} -2 & 4 & 5\\ -6 & 12 & 15\\ 12 & -24 & -30 \end{pmatrix}.\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-4cc684e96692d31379fdf8a18c8593c3_l3.png)
To pomeni, da je res ![]() .
.