12 Zveznost
Definicija 12.1: Naj bo ![]() poljubna točka intervala
poljubna točka intervala ![]() in
in ![]() dana funkcija. Rečemo, da je funkcija
dana funkcija. Rečemo, da je funkcija ![]() zvezna v točki
zvezna v točki ![]() , če velja:
, če velja:
![]()
Pravimo, da je funkcija zvezna na intervalu ![]() , če je zvezna v vsaki njegovi točki.
, če je zvezna v vsaki njegovi točki.
Izrek 12.1 [5,9]: Funkcija ![]() je v točki
je v točki ![]() zvezna natanko tedaj, ko je
zvezna natanko tedaj, ko je
![]()
Primer 12.1: Določimo ![]() in
in ![]() tako, da bo funkcija
tako, da bo funkcija ![]() , podana s predpisom
, podana s predpisom
![Rendered by QuickLaTeX.com \[f(x) =\begin{cases} ax^2-3b,&\textup{\v ce je }x>4, \\ 19,&\textup{če je }x=4,\\ 2ax-11b,&\textup{\v ce je }x<4, \end{cases}\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-ada4a54e24bdc0481f1eff2f42d1ce4f_l3.png)
zvezna v točki ![]() .
.
Izračunamo levo in desno limito dane funkcije v točki ![]() :
:
![]()
![]()
Funkcija ![]() je zvezna v točki
je zvezna v točki ![]() natanko tedaj, ko je
natanko tedaj, ko je ![]() . Torej,
. Torej, ![]() in
in ![]() .
.
Lastnosti zveznih funkcij
- Če sta funkciji
 in
in  zvezni v točki
zvezni v točki  , so v tej točki zvezne tudi funkcije
, so v tej točki zvezne tudi funkcije
![Rendered by QuickLaTeX.com \[f+g,\quad f-g,\quad f \cdot g,\quad \frac{f}{g}~(\textup{če je }g(x_0) \neq 0).\]](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-c2a503bf727c2bebe9ee734656597d21_l3.png)
- Če je funkcija
 zvezna v točki
zvezna v točki  in je funkcija
in je funkcija  zvezna v točki
zvezna v točki  , torej je tudi funkcija
, torej je tudi funkcija  , ker je
, ker je 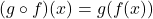 , zvezna v točki
, zvezna v točki  .
. - Vse elementarne funkcije so zvezne:
linearna, potenčna, polinomska, eksponentna, logaritemska ter sinusna in kosinusna funkcija. - Če je
![Rendered by QuickLaTeX.com f: [a,b] \longrightarrow \mathbb{R}](https://books.ung.si/app/uploads/quicklatex/quicklatex.com-30216e3d0ac9b2a985844715d9e6768b_l3.png) zvezna funkcija in je
zvezna funkcija in je 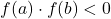 , torej ima funkcija
, torej ima funkcija  na tem intervalu vsaj eno ničlo.
na tem intervalu vsaj eno ničlo.
Primer 12.2: Ima polinom ![]() na intervalu
na intervalu ![]() ničlo?
ničlo?
Polinomska funkcija ![]() je zvezna in
je zvezna in ![]() ter
ter ![]() . Ker je
. Ker je ![]() , sledi, da ima
, sledi, da ima ![]() na intervalu
na intervalu ![]() eno ničlo.
eno ničlo.
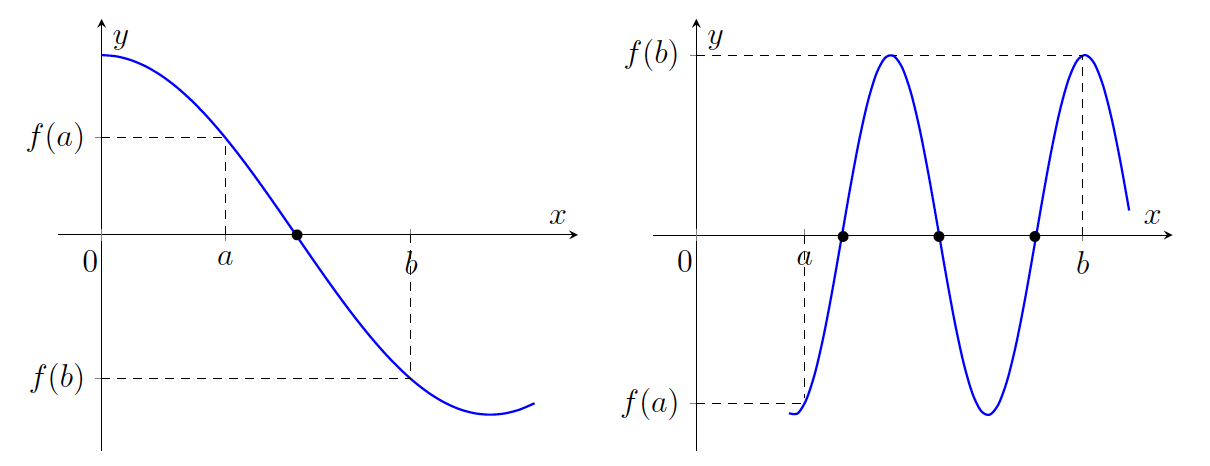
Primer 12.3: Dokažimo, da ima enačba ![]() na intervalu
na intervalu ![]() vsaj dve rešitvi.
vsaj dve rešitvi.
Polinomska funkcija ![]() je zvezna in
je zvezna in ![]()
Ker je ![]() , sledi, da obstaja
, sledi, da obstaja ![]() tako, da je
tako, da je ![]() . Podobno velja: ker je
. Podobno velja: ker je ![]() , obstaja
, obstaja ![]() tako, da je
tako, da je ![]() Torej ima dana enačba na intervalu
Torej ima dana enačba na intervalu ![]() vsaj dve rešitvi
vsaj dve rešitvi ![]() in
in ![]() .
.
5. Če je ![]() zvezna funkcija, je na tem intervalu tudi omejena.
zvezna funkcija, je na tem intervalu tudi omejena.
Primer 12.4: Zadnja lastnost velja le, če je funkcija ![]() definirana na zaprtem intervalu. Prav zares, funkcija
definirana na zaprtem intervalu. Prav zares, funkcija ![]() , podana s predpisom
, podana s predpisom
![]()
je definirana na odprtem intervalu ![]() in tam je zvezna ter navzgor in navzdol neomejena:
in tam je zvezna ter navzgor in navzdol neomejena:
![]()
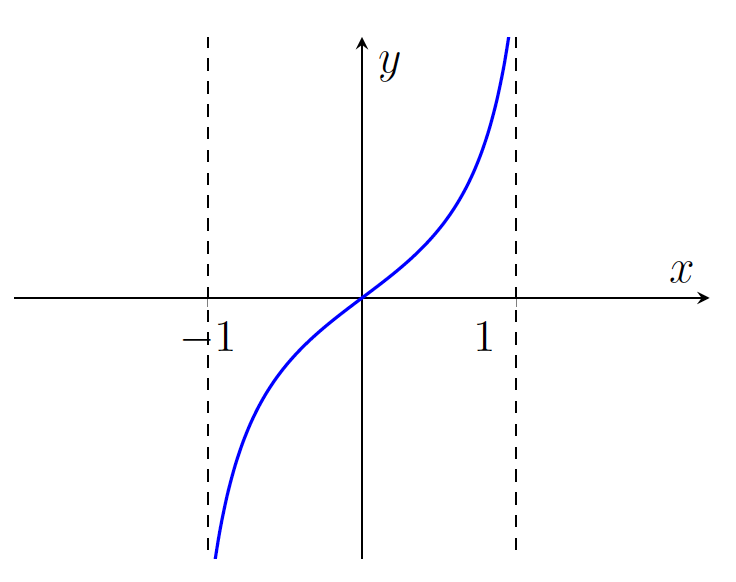
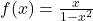 na intervalu
na intervalu 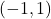 .
.6. Če je ![]() zvezna funkcija ter sta
zvezna funkcija ter sta ![]() (natančna spodnja meja) in
(natančna spodnja meja) in ![]() (natančna zgornja meja), potem obstajata točki
(natančna zgornja meja), potem obstajata točki ![]() in
in ![]() na intervalu
na intervalu ![]() tako, da je
tako, da je ![]() in
in ![]() .
.