4.5. Izbira in vrednotenje idej
Imre Cikajlo and Franc Gider
Zbrali smo veliko različnih idej, rešitev, ki so plod ustvarjalnega razmišljanja številnih članov tima. Vseh idej zaradi pomanjkanja časa, sredstev in možnosti za neuspeh ne moremo upoštevati, še manj uresničiti, zato moramo med številnimi možnostmi izbrati najprimernejšo, ki je v danem trenutku najboljša. Seveda v tej množici ni lahko prepoznati najboljše, saj pogosto še zdaleč ni očitna. Najustreznejšo rešitev izberemo po enem ali več merilih, ki so za nas pomembna. Merila vključimo v ustrezno orodje oz. tehnike, ki nam pomagajo pri izbiri najustreznejših idej za reševanje problema. Nekaj tehnik, ki tudi sodijo med orodja 6σ, je naštetih spodaj [13]:
- odločitveno drevo (ang. Decision Tree),
- primerjanje po parih (ang. Paired Comparison),
- mrežna analiza (ang. Grid Analysis),
- obteženo glasovanje (ang. Weighted Voting),
- šest mislečih klobukov (ang. Six Thinking Hats).
Izbrano idejo moramo čim bolj dodelati in jo razviti do stopnje, ko jo je mogoče tudi uresničiti. Tako izdelano idejo lahko precej natančno ocenimo in ovrednotimo ter ugotovimo, ali je tudi rentabilna, torej da se jo splača uporabiti. Če nam ne prinese pričakovanega učinka, jo moramo opustiti in izbrati drugo. Najpogosteje udejanjenje ideje in njen učinek ovrednotimo v denarju. V ta namen uporabimo tehniko:
- analiza stroškov in koristi (ang. Cost/Benefit Analysis).
Odločitveno drevo
Odločitveno drevo (ang. Decision Tree Analysis) nam je lahko v pomoč, kadar imamo na voljo veliko na videz dokaj podobnih možnosti. Pri tem razvijemo problem v drevesno strukturo, v kateri raziščemo različne možnosti in morebitne rešitve ovrednotimo, kar nam olajša izbiro. Hkrati dobimo orodje, ki nam prikazuje različne scenarije in ocene izidov posameznih scenarijev. Tako lahko poleg izida predvidimo tveganja, ki so povezana z vsakim scenarijem. To orodje zato uporabljamo pri izbiri strategij, projektov ali naložbenih priložnosti.
Odločitveno drevo lahko uporabimo tudi za razvoj novega izdelka. Če namreč analiziramo problem razvoja do vseh podrobnosti in pri tem predvidimo tveganja, smo lahko uspešnejši, kakor če novi izdelek prezgodaj pošljemo na trg.
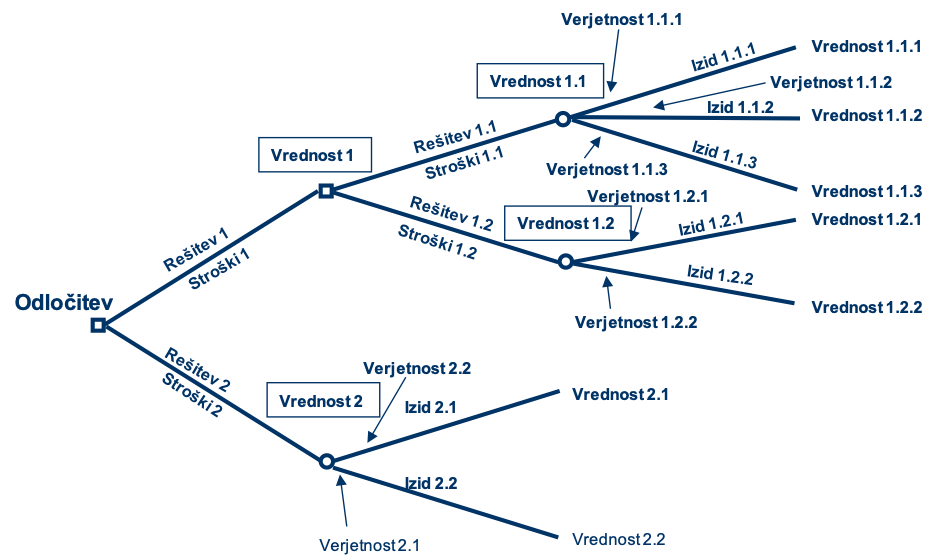
Risanje odločitvenega drevesa
V prvem koraku za problem, za katerega sprejemamo odločitev, predlagamo rešitve (rešitev 1, rešitev 2 – Slika 74), ki jih pod črto tudi opišemo. V drugem koraku jih natančneje ovrednotimo; če je rešitev zanesljiva, narišemo kvadratek in sprejmemo nadaljnje nove odločitve (rešitev 1.1 oz. rešitev 1.2 – Slika 74), če pa ni zanesljiva, narišemo krogec, ki ponazarja negotov izid. Pri slednjem imamo sicer več možnosti, vendar vsi izidi nastopijo le z neko verjetnostjo (Slika 75). Postopek nadaljujemo tako, da ovrednotimo vse možne rešitve.
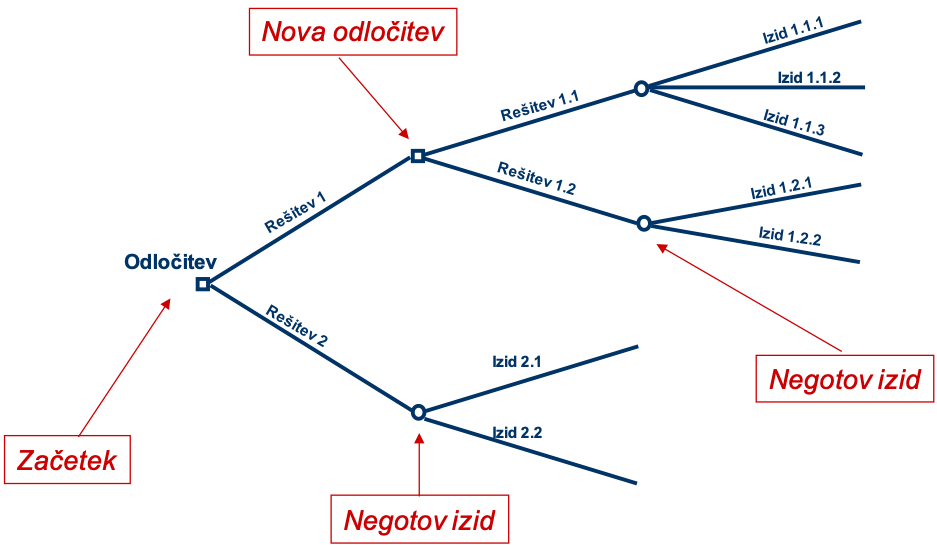
Vrednotenje odločitvenega drevesa
Vrednotenje odločitvenega drevesa pomeni, da posameznim izidom dodelimo vrednosti in verjetnosti (Slika 75). Pri vsakem krogcu, torej točki negotovega izida, ocenimo verjetnost izida. Če uporabljamo odstotke, mora biti vsota vseh izidov v vozlu negotovosti 100 %, če pa uporabljamo ulomke, mora biti vsota enaka 1. Če imamo na voljo podatke o preteklih vrednostih, lahko dokaj natančno ocenimo verjetnost izida, v nasprotnem primeru pa lahko damo le svojo subjektivno oceno.
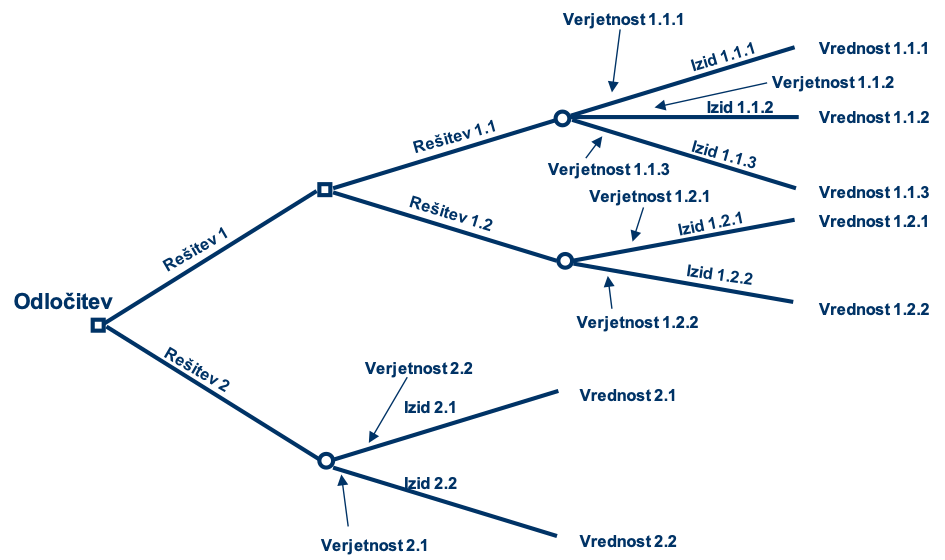
Izračun vrednosti vozlov
Najprej izračunamo vrednosti v vozlih negotovosti. To storimo tako, da ocenjene vrednosti v posameznih izdih pomnožimo z verjetnostjo teh izidov, izide posameznih zmnožkov pa seštejemo (Slika 76).
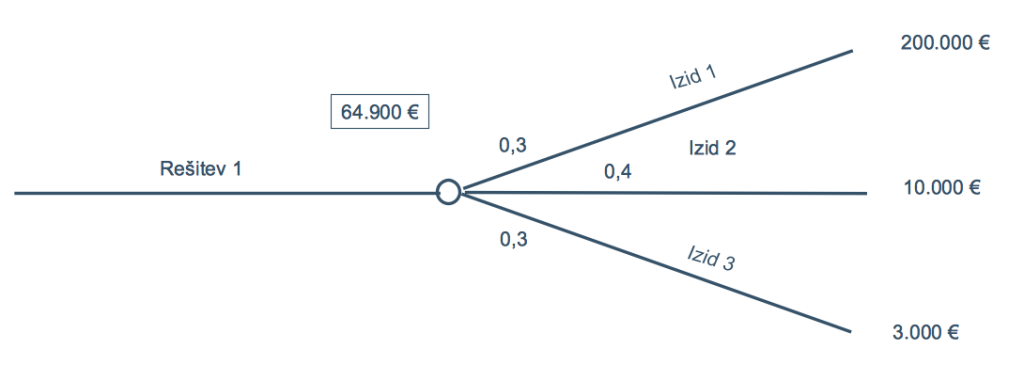
V primeru na Sliki 76 pomnožimo tri vrednosti (200.000, 10.000 in 3.000) z verjetnostmi (0,3, 0,4 in 0,3), da dobimo vrednost vozla negotovosti:
vrednost vozla = 0,3 * 200.000 + 0,4 * 10.000 + 0,3 * 3.000 = 64.900 €.
V drugem koraku izračunamo vrednosti odločitvenih vozlov. Vsaka od rešitev v odločitvenem vozlu je povezana s stroški. Ker gre v odločitvenem vozlu za predlog rešitve, pogosto lahko ocenimo tudi, kolikšni stroški bodo nastali pri udejanjenju. Če tega podatka nimamo, lahko damo svojo oceno.
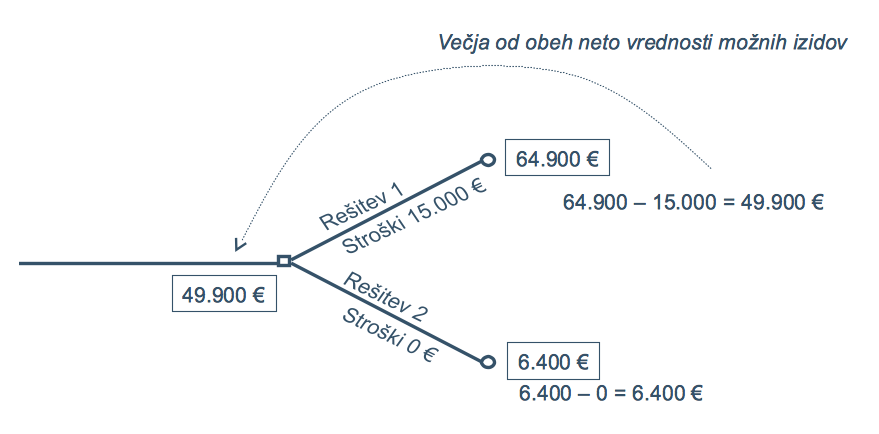
Vrednost odločitvenega vozla izračunamo tako, da od vrednosti veje, ki jo prinaša rešitev 1 (Slika 77), odštejemo stroške predlagane rešitve in jo primerjamo z vrednostjo veje, ki jo prinaša rešitev 2, zmanjšano za stroške rešitve. Kot vrednost odločitvenega vozla izberemo večjo vrednost:
vrednost vozla = večja od obeh neto vrednosti možnih izidov = 49.900.
Splošna formula za izračun vrednosti vozlov
Vrednosti posameznih vozlov negotovosti izračunamo tako, da vrednosti izidov pomnožimo s pripadajočimi verjetnostmi in jih seštejemo (Slika 78):
![]()
![]()
![]()
Potem izračunamo vrednosti odločitvenih vozlov po enačbi:
![]()
Končno odločitev v odločitvenem vozlu sprejmemo na podlagi večje vrednosti:
![]()
Primer 29:
V podjetju bi radi povečali dobiček. To lahko dosežejo na dva načina: z razvojem novega izdelka ali s konsolidacijo obstoječih izdelkov.
- Razvoj novega izdelka lahko izpeljejo na hitro ali počasi, temeljito.
- Konsolidacijo izdelkov lahko izvedejo na dva načina: z izboljšanjem obstoječih ali z umikom nekaterih izdelkov s trga.
S hitrim razvojem novega izdelka imajo 10 % možnosti za dober odziv trga, zaslužek pa ocenjujejo na 500.000 €, 20 % možnosti za srednji odziv trga in 25.000 € zaslužka ter 70 % možnosti za slab odziv trga in le 1.000 € zaslužka. Ob temeljitem razvoju so možnosti za zaslužek 500.000 € ob dobrem odzivu trga 40 %, 25.000 € ob srednjem odzivu trga 40 % in le 10.000 € ob slabem odzivu trga 20 %.
Pri konsolidaciji izdelkov sta dve poti: izboljšanje izdelkov prinese 200.000 € ob dobrem odzivu trga, a je možnosti za to 30 %, 10.000 € ob srednjem odzivu trga, za kar obstaja 40 % možnosti, in le 3.000 € zaslužka s 30 % možnosti ob slabem odzivu trga. Druga pot je umik izdelka s trga, ki lahko povzroči dober odziv (60 % možnosti) in prihranek 10.000 € ali slab odziv (40 % možnosti) in prihranek le 1.000 €.
Slika 79 prikazuje razdelane možnosti, ki so na voljo.
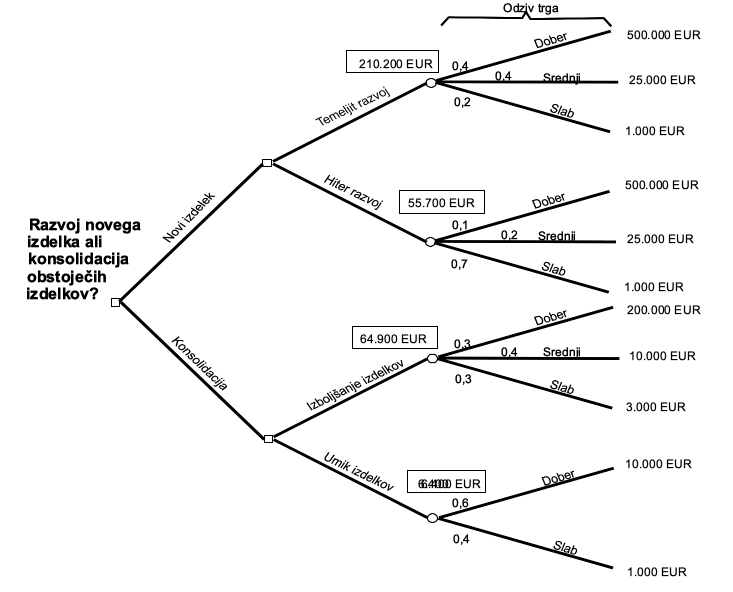
Iz danih možnosti (Slika 79) izračunamo vrednosti vozlov negotovosti pri temeljitem razvoju:
210.200 = 500.000 * 0,4 + 25.000 * 0,4 + 1.000 * 0,2
pri hitrem razvoju:
55.700 = 500.000 * 0,1 + 25.000 * 0,2 + 1.000 * 0,7
pri izboljševanju izdelkov:
64.900 = 200.000 * 0,3 + 10.000 * 0,4 + 3000 * 0,3
in pri umiku izdelkov s trga:
6400 = 10.000 * 0,6 + 1.000 * 0,4
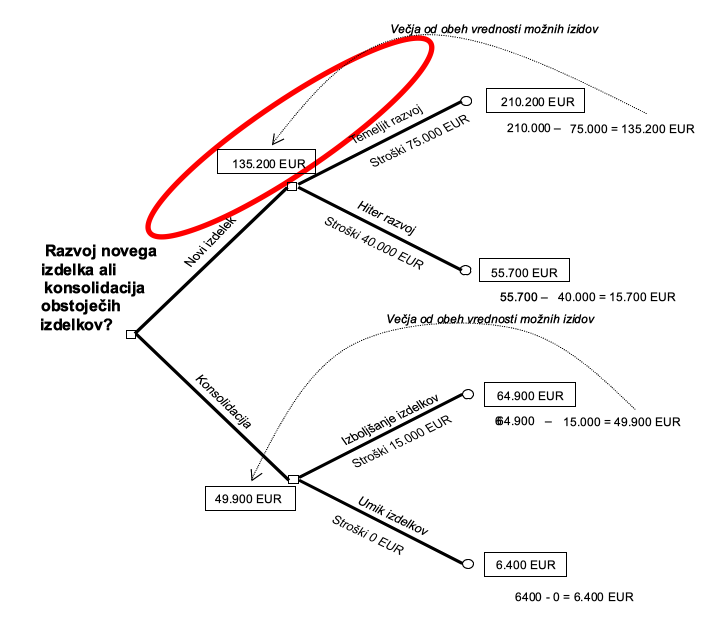
V nadaljevanju upoštevamo tudi stroške temeljitega razvoja – 75.000 € in hitrega razvoja – 40.000 € ter izračunamo vrednost odločitvenega vozla tako, da upoštevamo večjo vrednost posamezne veje. V našem primeru je to temeljiti razvoj novega izdelka z vrednostjo vozla 135.000 €.
Stroški konsolidacije pri izboljšanju izdelkov znašajo 15.000 €, pri umiku izdelka pa 0 €, zato je vrednost odločitvenega vozla 49.900 €.
Slika 80 prikazuje vrednosti vozlov in posameznih vej. Po primerjavi vrednosti odločitvenih vozlov za razvoj novega izdelka (135.000 €) in konsolidacijo izdelka (49.900 €) se odločimo za tisto možnost, ki prinaša večji zaslužek, torej za temeljiti razvoj novega izdelka, ki kljub največjim stroškom prinaša največji možni zaslužek, tj. 135.000 €.
Primer 30:
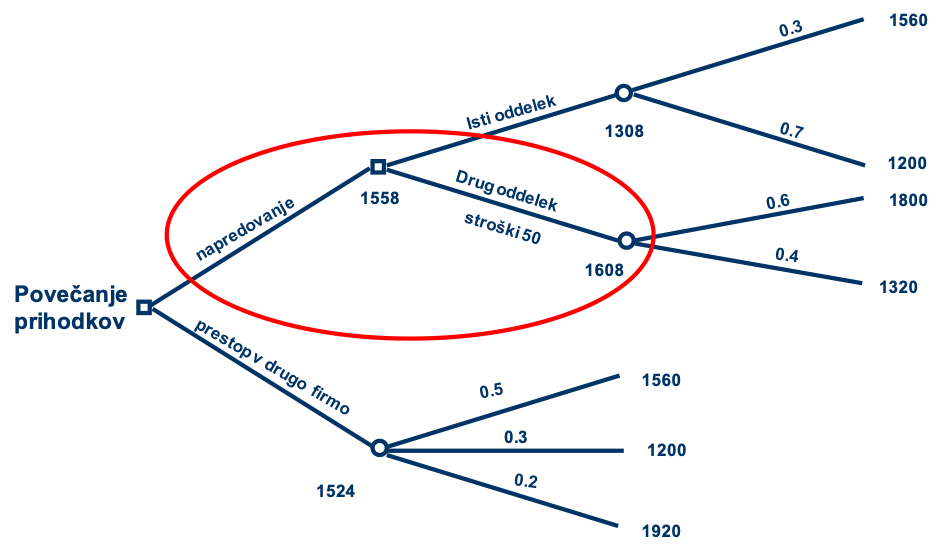
Po zaključku študija bi radi povečali svoje prihodke. Zdaj zaslužimo 100 € na mesec (1.200 € na leto). Prihodke lahko povečamo na dva načina (Slika 81):
- Napredovanje v obstoječem podjetju: v istem oddelku bi lahko zaslužili 30 € več na mesec, verjetnost za to je 30 %, v nasprotnem primeru ostanemo na istem. V drugem oddelku bi lahko zaslužili 50 € več na mesec (verjetnost 60 %) ali samo 10 € več na mesec (verjetnost 40 %). Za prehod v drugi oddelek se moramo dodatno naučiti španščine. Tečaj si moramo plačati sami in stane 50 €.
- Prestop v drugo podjetje: tam bomo z verjetnostjo 50 % dobili položaj, ki prinaša 30 € več na mesec, z verjetnostjo 30 % bomo na istem in z verjetnostjo 20 % bomo dobili 60 € več na mesec.
Z uporabo odločitvenega drevesa določimo najboljšo možno različico za večji zaslužek. Pri tem upoštevajmo zaslužek na letni ravni. Po izpeljani analizi ugotovimo, da je najdonosnejša možnost prehod v drugi oddelek in naložba v tečaj španskega jezika.
Odločitveno drevo ob upoštevanju »zdrave pameti« ponuja recept za učinkovito sprejemanje odločitev, ker:
- jasno opredeljuje problem in pokaže na možne izzive,
- dopušča analizo posledic odločitev,
- ovrednoti vrednosti izidov in verjetnost njihove uresničitve,
- na podlagi informacij, ki so na voljo, oz. dobrih ugibanj ponudi najboljšo rešitev.
Odločitveno drevo kot orodje za razvrščanje vhodnih podatkov na podlagi modela iz podatkovnih tabel lahko izdelamo tudi z orodji strojnega učenja (ang. Machine Learning). Iz podatkovne tabele, v kateri so podatki o osebah, njihovi starosti, nacionalnosti, izkušnjah, razberemo, ali se bodo dogodka udeležili (DA/NE) in kako verjetno je to (1–10):
| Starost | Izkušnje | Verjetnost | Nacionalnost | Udeležba |
|---|---|---|---|---|
| 36 | 10 | 9 | VB | NE |
| 42 | 12 | 4 | ZDA | NE |
| 23 | 4 | 6 | NOR | NE |
| 52 | 4 | 4 | ZDA | NE |
| 43 | 21 | 8 | ZDA | DA |
| 44 | 14 | 5 | VB | NE |
| 66 | 3 | 7 | NOR | DA |
| 35 | 14 | 9 | VB | DA |
| 52 | 13 | 7 | NOR | DA |
| 35 | 5 | 9 | NOR | DA |
| 24 | 3 | 5 | ZDA | NE |
| 18 | 3 | 7 | VB | DA |
| 45 | 9 | 9 | VB | DA |
Če želimo na podlagi podatkov napovedati rezultat ali se bo določena oseba dogodka udeležila, potem to lahko storimo tudi z uporabo knjižnic programskega jezika Python. Uvozimo modul “Pandas”, ki nam omogoča branje oz uvoz t.i. “cvs” ali comma-separated-values podatkov. Če želimo izvesti matematične operacije s podatki, moramo neštevilčne podatke pretvoriti/prekodirati v številčne (npr. “VB” -> 0, “ZDA” -> 1, “NOR” -> 2), kar storimo v Pythonu s funkcijo map():
d = {‘VB’: 0, ‘ZDA’: 1, ‘NOR’: 2}
df[‘Nacionalnost’] = df[‘Nacionalnost’].map(d)
d = {‘DA’: 1, ‘NE’: 0}
df[‘Udeležba’] = df[‘Udeležba’].map(d)
Odločitveno drevo v Pythonu ustvarimo tako, da iz knjižnice “Scikit-learn” – “sklearn” uvozimo tree, in DecisionTreeClassifier. Za izris drevesa oz vseh grafov uporabimo knjižnico “matplotlib” in funkcijo pyplot (predhodno namestimo modul MatplotLib; npr. pip3 install matplotlib). Naslednja programska koda v programskem jeziku Python (prirejeno po w3school.com) nam izdela in izriše odločitveno drevo (Slika 82):
import pandas
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
df = pandas.read_csv(“decisiontree.csv”)
d = {‘VB’: 0, ‘ZDA’: 1, ‘NOR’: 2}
df[‘Nacionalnost’] = df[‘Nacionalnost’].map(d)
d = {‘DA’: 1, ‘NE’: 0}
df[‘Udelezba’] = df[‘Udelezba’].map(d)
features = [‘Starost’, ‘Izkusnje’, ‘Verjetnost’, ‘Nationality‘]
X = df[features]
y = df[‘Udelezba’]
dtree = DecisionTreeClassifier()
dtree = dtree.fit(X, y)
tree.plot_tree(dtree, feature_names=features)
plt.show()
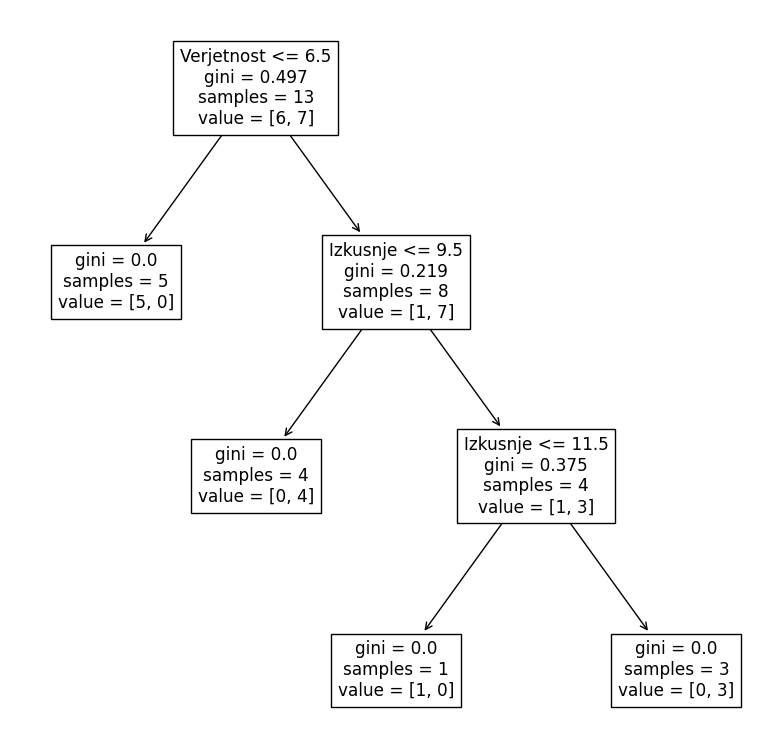
Kako deluje?
Če je Verjetnost” pod 6,5, potem je vrednost odločitvenega bloka pozitivna “True”, gini predstavlja ločitveno funkcijo z vrednostjo med 0 in 0,5; 0 pomeni, da so vsi vzorci enakoobravnavani, 0,5 pomeni, da jih 50 % ustreza kriteriju, 50 % po ne. Izhodne vrednosti (“values”) pa nam povedo, koliko izmed vhodnih podatkov ustreza (“DA” -7) in koliko ne (“NE” -6). Gini metrična methoda za klasifikacijo vzorca deluje po enačbi:
![]() ,
,
kjer je x število ustreznih podatkov (v našem primeru “DA”) in y število neustreznih (v našem primeru “NE”), n pa število vseh vzorcev.
V primeru “False” oz. če je “Verjetnost” več kot 6,5, klasificiramo na podlagi “Izkušenj”. Algoritem nam tukaj klasificira podatke 1 : 7 in nadaljuje naprej. Torej imamo 4 podatke z verjetnostjo več kot 6,5 in izkušnjami 9,5+. Po naslednji klasifikaciji ugotovimo, da ostanejo 3, ki imajo 11,5+ izkušenj, in 1, ki ima manj. To bi torej pomenilo, da bi 3 prejeli “DA” in 1 “NE”.
Za primer poglejmo, kako bi se naš sistem z odločitvenim drevesom odzval, če bi 40-letni Američan z 10-letnimi izkušnjami in verjetnostjo udeležbe 7 povprašal za udeležbo:
print(dtree.predict([[40, 10, 7, 1]]))
sistem vrne [1], kar pomeni “DA” oz. Američan se bo prireditve udeležil. Kaj pa če istemu človeku zmanjšamo “Verjetnost” udeležbe na 6:
print(dtree.predict([[40, 10, 6, 1]]))?
Potem je rezultat [0], kar pomeni “NE” oz. sistem Američanu odsvetuje udeležbo.
Primerjanje po parih
Kadar izbiramo med številnimi idejami ali rešitvami in moramo izbrati najboljšo, se lahko odločimo za tehniko primerjanja po parih (ang. Paired Comparisons) in primerjamo možnosti vsako z vsako. Tako ugotovimo, kako pomembna je izbrana možnost v primerjavi z drugimi. Metoda primerjanja po parih je precej preprosta in dokaj nezanesljiva, saj temelji zgolj na presojanju in izkušnjah, ne vključuje pa objektivnih kazalnikov ali prednostnih dejavnikov. Uporabljamo jo, kadar nimamo na voljo objektivnih podatkov, na podlagi katerih bi sprejemali odločitve.
S tehniko primerjanja po parih določimo rešitev izbranega problema, ki bo imela največji učinek.
- Naredimo seznam vseh možnosti (idej, rešitev …) in vsaki dodelimo eno črko:
- A – možnost 1
- B – možnost 2
- C – možnost 3
- D – možnost 4
- Narišemo tabelo (Slika 83) z vsemi možnostmi v vrsticah in stolpcih:
Slika 83. Tabela primerjanja možnosti po parih - Pobarvamo polja, v katerih bi posamezno možnost primerjali samo s sabo. Ta polja tečejo po diagonali od zgornjega levega do spodnjega desnega kota tabele (Slika 84).
Slika 84. Primerjanje po parih – samih s sabo ne primerjamo -
Pobarvamo polja, v katerih bi se primerjave podvajale. Ta polja so pod diagonalo (Slika 85).
Slika 85. Primerjanje po parih – izločimo možnost podvajanja - Primerjamo med sabo možnosti v koloni in stolpcu (Slika 86). Razliko ovrednotimo s številkami od 0 (ni razlike) do 3 (zelo velika razlika).
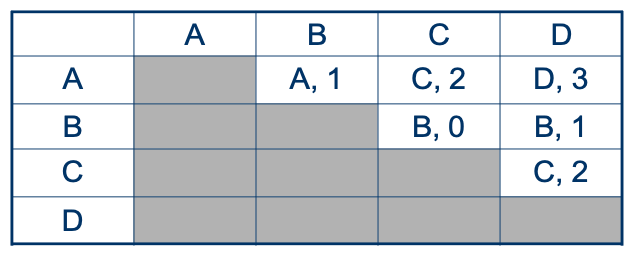
Slika 86. Primerjanje po parih – vrednotenje razlik med možnostmi -
Zberemo točke za vsako možnost iz vseh polj.
- Izberemo možnost, ki je dobila največ točk.
Rezultate predstavimo v tabeli (Slika 87):

Primer 31:
Podjetnik išče možnosti za razvoj in širjenje svoje dejavnosti (Slika 88). Možnosti so omejene. Po premisleku pride do teh rešitev:
- začetek prodaje na tujih trgih (A),
- povečana prodaja na domačem trgu (B),
- izboljšanje storitev za stranke (C),
- izboljšanje kakovosti izdelkov (D).

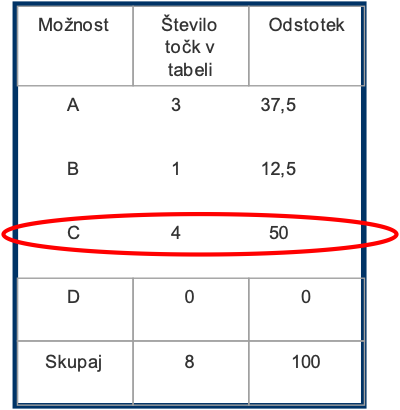
Po opravljeni analizi primerjanja po parih se izkaže, da je najboljša možnost C – izboljšanje storitev za obstoječe stranke (Slika 89).
Mrežna analiza
Mrežna analiza (ang. Grid Analysis) je na videz zelo podobna tehniki primerjanje po parih, ki nam pomaga pri odločanju. Njuna razlika je v tem, da mrežna analiza upošteva tudi prednostne dejavnike, ki jih postavi ocenjevalec [20].
To tehniko uporabimo takrat, ko imamo na voljo več dobrih možnosti in številne dejavnike, ki jih pri odločitvi upoštevamo. Najprej naredimo seznam vseh možnosti za reševanje problema:
| – Možnost 1 | – Dejavnik 1 |
| – Možnost 2 | – Dejavnik 2 |
| – Možnost 3 | – Dejavnik 3 |
| – Možnost 4 | – Dejavnik 4 |
| – Dejavnik 5 |
V nadaljevanju narišemo tabelo, v katero zapišemo možnosti v prvi stolpec, dejavnike pa v prvo vrstico. Ocenimo možnosti po vseh dejavnikih od 0 (slabo) do 3 (zelo dobro):
| Dejavnik 1 | Dejavnik 2 | Dejavnik 3 | Dejavnik 4 | Dejavnik 5 | Skupaj | |
|---|---|---|---|---|---|---|
| Teža | 1 | 2 | 3 | 4 | 5 | |
| Možnost 1 | 0 | 2 | 1 | 2 | 1 | 20 |
| Možnost 2 | 1 | 3 | 3 | 3 | 1 | 33 |
| Možnost 3 | 1 | 1 | 0 | 0 | 1 | 8 |
| Možnost 4 | 3 | 2 | 0 | 2 | 1 | 20 |
Ko smo tabelo dopolnili z ocenami možnosti, določimo še relativno pomembnost dejavnikov; ta ocena je pogosto subjektivna. Nato izberemo tisto možnost, ki smo ji namenili največ točk.
Število točk izračunamo po formuli:
![]()
V zgornjem primeru je torej najboljša možnost 2. Skupno število točk smo dobili takole:
1 * 1 + 3 * 2 + 3 * 3 + 3 * 4 + 1 * 5 = 33.
Primer 32:
Navdušenec nad deskanjem na vodi hoče zamenjati avtomobil. Rad bi kupil takega, s katerim ne bo mogel prevažati le svoje opreme za deskanje, ampak bo uporaben tudi za poslovna potovanja. Vedno so mu bili všeč avtomobili brez strehe. Toda noben avtomobil ne ustreza vsem trem zahtevam.
Možnosti, ki jih ima na voljo:
- avtomobil s štirikolesnim pogonom in trdo streho,
- udoben družinski avtomobil,
- enoprostorski avtomobil,
- športni avtomobil.
Dejavniki, po katerih bo izbiral novi avtomobil:
- cena,
- sposobnost prevoza jadralne deske pri normalni hitrosti vožnje,
- sposobnost varnega hranjenja opreme za deskanje,
- udobnost na daljših potovanjih,
- zabava,
- lep videz in kakovost avtomobila.
| Cena | Deska | Hranjenje | Udobje | Zabava | Videz | Skupaj | |
|---|---|---|---|---|---|---|---|
| Teža | 4 | 5 | 1 | 2 | 3 | 4 | |
| Športni avtomobil | 1 | 0 | 0 | 2 | 3 | 3 | 29 |
| Avtomobil s štirikolesnim pogonom | 0 | 3 | 2 | 2 | 1 | 1 | 29 |
| Družinski avtomobil | 2 | 2 | 1 | 3 | 0 | 0 | 24 |
| Enoprostorni avtomobil | 2 | 3 | 3 | 3 | 0 | 1 | 36 |
Po opravljeni analizi navdušenec nad deskanjem ugotovi, da je najboljša izbira (glede na izbrane dejavnike in njihovo prioriteto) enoprostorski avtomobil.
Obteženo glasovanje
Obteženo glasovanje (ang. Weighted Voting) je tehnika, s katero zmanjšamo število predlaganih možnih rešitev, pri čemer odločajo vsi člani projektne skupine. Odločanje izvedemo z glasovanjem, ki je lahko tajno ali javno, člani tima pa lahko glasujejo za eno ali več možnosti. Tehnika je preprosta za uporabo, ker za izbiro najustreznejše možnosti ni treba razvijati posebnih meril, prav tako pa zanjo ne potrebujemo nobenih posebnih pripomočkov.
Obteženo glasovanje najpogosteje uporabljamo za doseganje soglasja med člani projektnega tima. Izvedemo ga takole:
- Naredimo seznam vseh možnosti.
- Vsakemu udeležencu dodelimo število glasov, ki jih ima na voljo (običajno 1,5 krat število možnosti).
- Vsak udeleženec podeli glasove med razpoložljive možnosti. Vsaki možnosti dodeli vsaj 1 glas.
- Izid glasovanja vpišemo v matriko.
Primer 33:
- Izbiramo med šestimi možnostmi.
- Vsaka oseba ima 9 glasov (1,5 krat število možnosti).
- Vsak član mora vsaki možnosti dati vsaj 1 glas.
- Skupina je najvišje ocenila možnosti 4, 1 in 2.
- Po glasovanju bo skupina kvantitativno ocenjevala možnosti 4, 1 in 2.
| Možnosti za izboljšave | Bojan | Vesna | Tomaž | Nada | Tone | Skupaj |
|---|---|---|---|---|---|---|
| Sprememba na stroju | 1 | 2 | 2 | 3 | 1 | 9 |
| Usposabljanje za SPC | 3 | 1 | 1 | 1 | 2 | 8 |
| Skrajšanje časa nastavitev | 2 | 1 | 1 | 1 | 1 | 6 |
| Izboljšanje procesa odločanja | 1 | 2 | 3 | 2 | 2 | 10 |
| Zmanjšanje čakalnih vrst | 1 | 2 | 1 | 1 | 1 | 6 |
| Izboljšati izkoristek materiala | 1 | 1 | 1 | 1 | 2 | 6 |
| Skupaj | 9 | 9 | 9 | 9 | 9 | 45 |
Šest mislečih klobukov
Šest mislečih klobukov (ang. Six Thinking Hats) je izvrstna tehnika, s katero preučimo učinke posamičnih odločitev iz različnih zornih kotov. Dovoljuje dobršno mero skepticizma in čustvenih mnenj, kar izključuje popolnoma razumske odločitve in tako odpira možnosti za ustvarjalno mišljenje pri sprejemanju odločitev, npr. pesimisti se naravnajo pozitivno z ustvarjalnimi idejami. Tehnika mislečih klobukov omogoči, da izločimo osebno mišljenje posameznikov in celoten projektni tim usmerimo v reševanje problema. Namen te tehnike je namreč zagotoviti osredotočenost tima na problem in preprečevanje negativnih pogledov na rešitve. Tehniko je razvil Edward de Bono [17] v zgodnjih 80. letih.
Bistvo »šestih mislečih klobukov« je šest različnih načinov razmišljanja. Celoten tim, ki v danem trenutku rešuje problem, hkrati nosi klobuke iste barve in razmišlja na enak način. Nato klobuke zamenjajo, zamenjajo pa tudi način razmišljanja. Kako, kdaj in v kakšnem vrstnem redu se zamenjajo klobuki, je odvisno od moderatorja. Ta narekuje, kateri klobuk v nekem trenutku nosi tim. Seveda mora biti moderator izkušen vodja in dober poznavalec problema, ki ga rešujejo; od vrstnega reda uporabe klobukov je namreč odvisna marsikatera posredno porojena ideja.
Šest mislečih klobukov – pomen
|
Bela barva Govorimo samo o podatkih in informacijah, ki so na razpolago. Lastna mnenja pustimo ob strani. Klobuk nam odpre objektivni pogled. |
Rdeča barva Govorimo o svojih občutjih glede problema in rešitev, vendar ne razlagamo občutij. Klobuk nam pomaga predvideti tveganja. |
| Črna barva
Kritiziramo rešitve. Klobuk nam pomaga poiskati nestvarne rešitve. |
Modra barva Naredimo povzetek povedanega. Klobuk uporabimo, ko moramo oblikovati konkretne zaključke. |
|
Zelena barva Govorimo o novih idejah. Zelena spodbuja ustvarjalnost. Klobuk uporabimo, ko potrebujemo nove ideje in ustvarjalnost. |
Rumena barva O idejah govorimo pozitivno. Rumena spodbuja optimizem. Klobuk uporabimo, ko govorimo o prednostih predlagane rešitve. |
Šest mislečih klobukov – postopek
Na prvi stopnji analize je najpomembnejše, da dobro predstavimo problem, ki ga želimo obravnavati. Potem ravnamo po spodaj naštetih korakih:
- Uporabimo modri klobuk in se dogovorimo o vrstnem redu uporabe klobukov drugih barv. Ta vrstni red ima namreč precejšen vpliv na porajanje dodatnih idej.
- Uporabimo klobuke iste barve za vse člane tima. Tim razpravlja o problemu iz različnih zornih kotov glede na to, kakšne klobuke uporablja v danem trenutku,
- Pri razpravi zapisujemo ključne ideje in ugotovitve za vsak posamezen klobuk.
- Na koncu z uporabo modrega klobuka naredimo povzetek razprave.
Primer 34:
Skupina je razpravljala o zamisli, da bi oblikovali reklamo za hotel Slon s slonom, ki bi ga vodili po ulicah. Slika 90 prikazuje nekaj točk pri posamezni barvi klobukov.
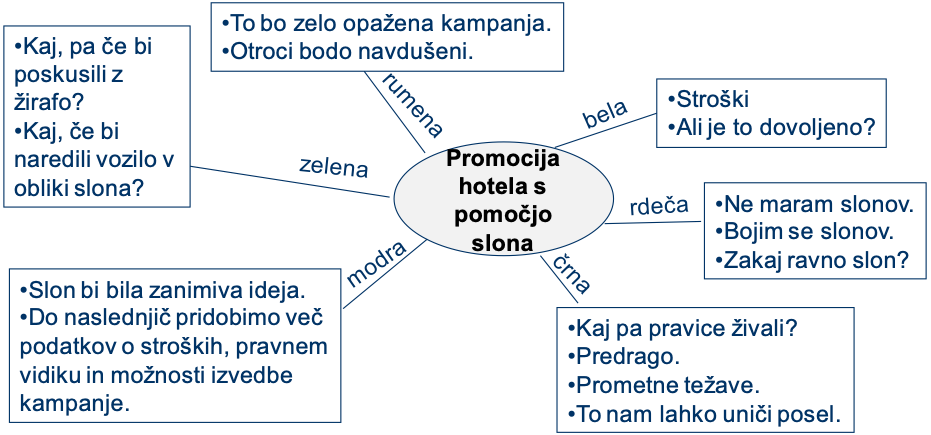
Iz primera vidimo, da je tim promocijsko zamisel glede hotela slon osvetlil iz različnih zornih kotov. Na koncu analize (pod modrim klobukom) si je zadal naloge, ki jih mora opraviti do naslednjič.
Analiza stroškov in koristi
Porajanje in izbiranje idej mora biti ustvarjalen proces, saj na ta način lahko pridemo do izrednih inovacij, ki zagotavljajo novo dodano vrednost ali rešitev problema, ki je v procesu povzročal težave. Ker pa izbrane ideje pogosto niso gospodarne, kajti za njihovo uresničitev bi porabili preveč denarja oz. rešitev problema ne bi prinesla omembe vrednega denarnega prihranka [21], je treba izbrano idejo vnaprej ovrednotiti glede na stroške in koristi, ki bi jih prinesla. Tako pri analizi stroškov in koristi (ang. Cost/Benefit Analysis) seštejemo na eni strani vse morebitne stroške uresničenja ideje, na drugi pa vse učinke, ki bi jih pri tem imeli. Učinke izbrane ideje oz. rešitve analiziramo v določenem obdobju (npr. 5 let) in izračunamo čas, v katerem se naložba povrne.
- Stroški razvoja – so enkratni stroški ob razvoju sistema, ki se ne pojavljajo po tem, ko je bil sistem že razvit.
Primeri:
-
- plače razvijalcev in drugega osebja,
- uporaba računalnikov,
- izobraževanje,
- cena strojne in programske opreme ter materiala …
- Stroški obratovanja – so ponavljajoči se stroški, ki nastajajo ob rednem delovanju oziroma uporabi novitete. Delimo jih na stalne in spremenljive.
- Stalni (fiksni) stroški so tisti, katerih višina je enaka ne glede na obseg poslovanja (npr. stroški najema poslovnega prostora so odvisni od kvadrature prostora in so enaki ne glede na to, ali v prostoru naredimo 50 ali 100 izdelkov):
- o plače za zaposlene,
- o vzdrževanje prostorov,
- o najemnine, licence ipd.
- Spremenljivi (variabilni) stroški so tisti, katerih višina je odvisna od obsega poslovanja (npr. za izdelavo 100 kosov izdelka porabimo več materiala kakor za izdelavo 50 kosov):
- o uporaba strojev,
- o gorivo, energija,
- o material,
- o uporaba računalnikov (najem linij, CPU, terminalov …),
- o potrošni material,
- o stroški za vzdrževanje, za telefon …
- Koristi:
Neposredne koristi (ang. tangible benefits) so tiste, ki jih lahko neposredno ovrednotimo (npr. če pri enem izdelku prihranimo 10 % materiala, lahko to pri izdelanih 100 kosih neposredno ovrednotimo v denarju):
- o mesečni oz. letni prihranki, neposredni dobiček …,
- o manj napak pri obdelavi podatkov, manj porabe materiala, povečanje prodaje, zmanjšanje stroškov …
Posredne koristi (ang. intangible benefits) so tiste, ki jih neka izboljšava prinese podjetju in jih težko ovrednotimo neposredno (npr. pri uvedbi prožnega delovnega časa za zaposlene v našem podjetju težko ovrednotimo neposredne prihranke. Bo pa takšna poteza zagotovo ugodno vplivala na zadovoljstvo zaposlenih, kar bo posredno povečalo kakovost njihovega dela in hkrati tudi ugled podjetja pri kupcih, ki se bodo pogosteje odločali za sodelovanje s podjetjem):
- o zadovoljnejši kupci,
- o izboljšanje morale zaposlenih,
- o izboljšanje varnosti pri delu,
- o zmanjšanje obremenitve okolja …
- Časovna vrednost denarja:
»Dolar danes je vreden več kakor dolar čez eno leto« je eden najpomembnejših izrekov v menedžmentu, ko govorimo o naložbah.
Cena razvoja raste po njegovi uvedbi – danes porabljeni denar bi imel čez čas dejansko večjo vrednost.
Finančne koristi novega sistema rastejo s časom – danes privarčevani denar ima čez čas dejansko večjo vrednost.
To pomeni, da gledamo na denar kot na investicijska sredstva, s katerimi lahko povečamo svoj kapital. Če ga ne plemenitimo s svojimi idejami oz. naložbami, ga lahko prepustimo npr. bankam ali drugim investitorjem. Ti bodo vlagali naš denar in nam prislužili kapitalski dobiček, v zameno za svojo storitev pa nam bodo zaračunali odstotek provizije. Vse stroške in koristi projekta moramo preračunati na današnjo vrednost, kajti le tako lahko primerjamo projekte, katerih razvoj in izkoriščanje učinkov trajata različno dolgo.
Sedanja vrednost denarja
PVn = sedanja vrednost denarja n let od danes
i = obrestna mera
V = znesek denarja, sedanjo vrednost katerega želimo izračunati
![]()
Primer:
Recimo, da bomo dobili 1.000 € čez 3 leta. Koliko bi bil ta denar vreden danes, če je povprečna obrestna mera na bankah 5 %?
![]()
Kaj pa, če bi isti denar imeli šele čez pet let?
![]()
Primer analize stroškov/koristi na podlagi sedanje vrednosti denarja:
Uvesti hočemo nov informacijski sistem, čigar trajanje je 6 let.
Sestavimo tabelo stroškov in koristi za 6 let in pri tem upoštevamo obrestno mero 12 %. Vse stroške in koristi moramo preračunati na sedanjo vrednost, nato pa prikazati skupno vrednost stroškov in koristi uvedbe sistema po letih.
Najprej oblikujemo tabelo, v kateri bomo spremljali stroške, nastale s projektom na začetku in v letih uporabe sistema.
| Leto | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Prihodki in odhodki | |||||||
| Stroški razvoja | -418.040 | ||||||
| Stroški vzdrževanja | -15.054 | -20.000 | |||||
| obratni faktor 12 % | |||||||
| Sedanja vrednost stroškov | |||||||
| Kumulativna sedanja vrednost stroškov | |||||||
| Koristi uvedbe sistema | 0 | 150.000 | 230.000 | 250.000 | |||
| Sedanja vrednost koristi | |||||||
| Kumulativna sedanja vrednost koristi | |||||||
| Kumulativna cena, preračunana na sedanjo vrednost |
V tabelo vpišemo stroške razvoja (418.040 USD) in vzdrževanje za vseh šest let (v prvem letu 15.054 USD, nato pa stroški vzdrževanja vsako leto narastejo do 20.000 USD v šestem letu). Izračunamo obrestni faktor za vsako leto posebej in vpišemo neposredne koristi uvedbe sistema za vsako leto posebej (ocenjeni prihranki od projekta naraščajo od 150.000 USD v prvem letu do 250.000 USD v šestem letu).
Izračunamo sedanjo vrednost stroškov za vsako leto posebej, nato jih seštejemo in dobimo celotno vrednost stroškov, preračunano na današnjo vrednost denarja (488.689 USD). Prav tako izračunamo sedanjo vrednost koristi (795.315 USD). Nazadnje odštejemo skupne stroške od skupne vrednosti koristi po letih in dobimo skupno ceno, preračunano na sedanjo vrednost (306.625 USD). Tako je iz tabele razvidno, da se naložba povrne približno po treh letih, ko že ustvarjamo dobiček.
Finančna analiza projekta
S finančno analizo projekta pridobimo podatke, ki so pomembni za odločanje glede sprejetja sklepa o uresničitvi ideje oz. rešitve. Med pomembnejše finančne kazalnike ideje prištevamo:
- Analiza dobe odplačevanja (ang. Payback Time – PBT)
- Kdaj bodo koristi izplačale stroške?
- Obdobje odplačila.
- Naložbeni donos (ang. Return of Investment – ROI)
- Odstotek, ki izraža razmerje med vloženim in dobljenim v predvidenem času uporabe sistema.
- ROI = (ocenjene celotne koristi – ocenjeni celotni stroški) / ocenjeni celotni stroški.
- Neto sedanja vrednost (ang. Net Present Value – NPV)
- Naložbeni donos (kot absolutno število).
Pri tem nas zanima le, kdaj bo naložba v novo idejo ali rešitev poplačana s koristmi, ki jih prinaša. Izračunamo točko preloma oz. prag rentabilnosti (ang. break-even point), ki nam da informacijo o dobi odplačila naložbe.
![]()
![]()
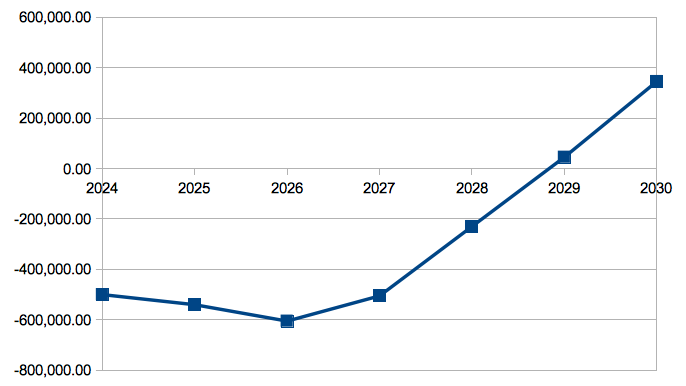
Iz grafa (Slika 92) vidimo, da krivulja, ki prikazuje razliko med koristmi projekta in stroški, preide z negativnega na pozitivno območje po 2 letih in 9 mesecih. Ta točka na grafu je točka preloma – čas, v katerem se nam s koristmi povrnejo denarna sredstva, ki smo jih vložili v projekt.
Naložbeni donos nam da informacijo o razmerju med pridobljenimi koristmi in vloženim kapitalom – odstotek, ki izraža razmerje med vloženim in dobljenim v predvidenem času uporabe sistema (oziroma naložbeni donos).
![]()
![]()
Iz zgornjega izračuna vidimo, da nam je projekt, v katerega smo vložili 488.689 USD, preračunano na sedanjo vrednost, prinesel 795.315 USD koristi. Naša naložba je torej v šestih letih imela donosnost 62 %.
Neto sedanja vrednost nam da informacijo o naložbenem donosu v absolutni obliki. Gre za znesek, ki ga izračunamo kot razliko med skupno vrednostjo koristi, preračunano na sedanjo vrednost, in naložbo s stroški v določenem obdobju, preračunano na sedanjo vrednost.
Iz grafa odčitamo skupno ceno, preračunano na sedanjo vrednost ob koncu določenega obdobja:
![]()
Primer 35:
Direktor prodaje se odloča, ali bi uvedel nov informacijski sistem za podporo prodaji. V oddelku imajo le nekaj računalnikov, zaposleni pa niso preveč vešči dela z njimi. Direktor se zaveda, da bi z uporabo računalniškega sistema lahko ponujali storitve več strankam, izboljšali pa bi tudi raven svojih storitev.
Direktor je izvedel analizo stroškov in koristi.
Stroški
Nova računalniška oprema:
- 10 računalnikov z osnovno programsko opremo po 1.225 EUR = 12.250 EUR,
- 1 strežnik po 1.750 EUR,
- 3 tiskalniki po 600 EUR vsak = 1.800 EUR,
- namestitev računalnikov 2.300 EUR,
- programska oprema za podporo prodaji 7.500 EUR.
Usposabljanje:
- spoznavanje računalnikov – 8 ljudi po 200 EUR vsak = 1.600 EUR,
- tečaj tipkanja – 8 ljudi po 200 EUR vsak = 1.600 EUR,
- uporaba programske opreme za podporo prodaji – 12 ljudi po 350 EUR vsak = 4.200 EUR.
Drugi stroški:
- izgubljeni čas: 40 ljudi po 70 EUR na dan = 2.800 EUR,
- izgubljena prodaja zaradi motenj pri postavitvi sistema: ocena 10.000 EUR,
- izgubljena prodaja zaradi privajanja v prvih mesecih: ocena 10.000 EUR.
Skupni stroški: 55.800 EUR.
Koristi
- trikratno povečanje zmogljivosti za pošiljanje pisem: ocena 20.000 EUR/leto,
- zmožnost izvajanja prodaje po telefonu: ocena 10.000 EUR/leto,
- povečana učinkovitost sledenja prodaji: ocena 25.000 EUR/leto,
- izboljšan servis za kupce in tako zadržanje kupcev: ocena 15.000 EUR/leto,
- točnejše informacije o kupcih: ocena 5.000 EUR/leto,
- lažje vodenje prodaje v podjetju: 15.000 EUR/leto.
Skupaj koristi: 90.000 EUR/leto.
Čas povrnitve naložbe: 55.800 EUR/90.000 EUR = 0,62 leta = pribl. 8 mesecev.
Glede na analizo bo direktor računalniški sistem verjetno uvedel. Zavedati pa se moramo, da so zgornje ocene o učinkih projekta subjektivne.
Primer 36:
V podjetju želimo investirati v odprtje raziskovalno-razvojnega oddelka. Zavedamo se, da je začetna investicija visoka, znaša 500.000 EUR, in da bodo prvih 6 let nastajali stroški 0 EUR (2024), 50.000 EUR (2025), 65.000 EUR (2026), 150.000 EUR (2027), 75.000 EUR (2028), 75.000 EUR (2029), 50.000 EUR (2030), koristi sistema pa bo podjetje občutilo postopoma: 0 EUR (2024), 10.000 EUR (2025), 0 EUR (2026), 250.000 EUR (2027), 350.000 EUR (2028), 350.000 EUR (2029) in 350.000 EUR (2030).
Izračunamo naložbe PBT, ROI in NPV pri ocenjenem 5-odstotnem letnem faktorju (Slika 91):
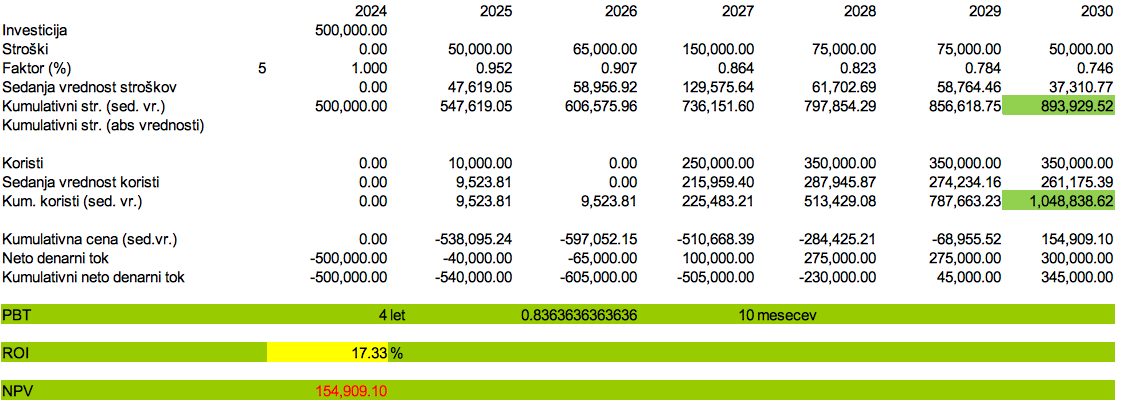
PBT = leto pred poplačilom + nepoplačani znesek/neto koristi v letu poplačila = 4 + (-230.000/275.000) = 4 leta in 10 mesecev
ROI = 17,33 %
Kratek kviz
