2 Orientacija po nebu
Jure Japelj and Andreja Gomboc
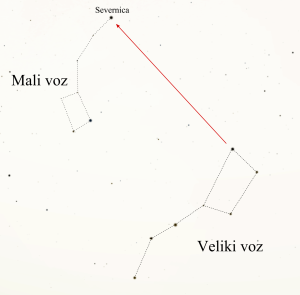
Iskanje telesa na nebu je podobno iskanju mesta na zemljevidu. Večja mesta na že znanem delu zemljevida najdemo brez težav: poiščemo znani vzorec, kot je na primer italijanski škorenj, se po njem orientiramo in najdemo iskani kraj. Podobno nam pri orientaciji po nebu pomagajo znani vzorci svetlih zvezd. Na primer, da želimo poiskati zvezdo Severnico (slika 2.1). Najprej poiščemo Veliki voz, enega izmed najopaznejših vzorcev zvezd (sam Veliki voz ni ozvezdje, pač pa je del ozvezdja Veliki medved). Dolžino prednje stranice približno petkrat podaljšamo navzgor in tako pridemo do repa Malega voza oziroma Severnice. Zvezdnato nebo postane z nekaj izkušnjami tako domače, da se na njem znajdemo brez težav in najdemo iskane zvezde.

Kaj pa, če želimo opazovati manj znano zvezdo? Ali pa smo odkrili novo supernovo in želimo drugim sporočiti, kje točno je na nebu? V tem primeru je bolj praktično položaj nebesnega telesa opisati s koordinatama. V astronomiji so že vrsto stoletij v uporabi nebesni koordinatni sistemi, s katerimi opisujemo položaj teles na nebu.
Veliki in mali krogi
Planeti, zvezde in galaksije so od nas različno oddaljeni. A vse te razdalje so tako zelo velike, da naš občutek za prostorsko porazdelitev nebesnih teles povsem odpove. Zato si smemo predstavljati, da nebesna telesa ležijo na površini velike (prozorne) sfere, v katere središču smo mi, ki opazujemo. Tej krogli rečemo nebesna sfera ali nebesna krogla.
Položaj telesa na krogli je točka. Točke lahko med seboj povežemo z loki. Loki so deli krogov, ki jih dobimo, če kroglo v mislih prerežemo. To lahko naredimo na dva načina. Če kroglo prerežemo na polovico, dobimo krog z največjim možnim polmerom, ki je enak radiju krogle. Takemu krogu rečemo veliki ali glavni krog. Če kroglo prerežemo tako, da dobimo dva različno velika dela, prerezu ustreza krog s polmerom, manjšim od polmera krogle. Takemu krogu rečemo mali krog. Primer velikega kroga je ekvator na površju Zemlje (slika 2.3 levo). Vsi krogi, ki so vzporedni ekvatorju, so mali.
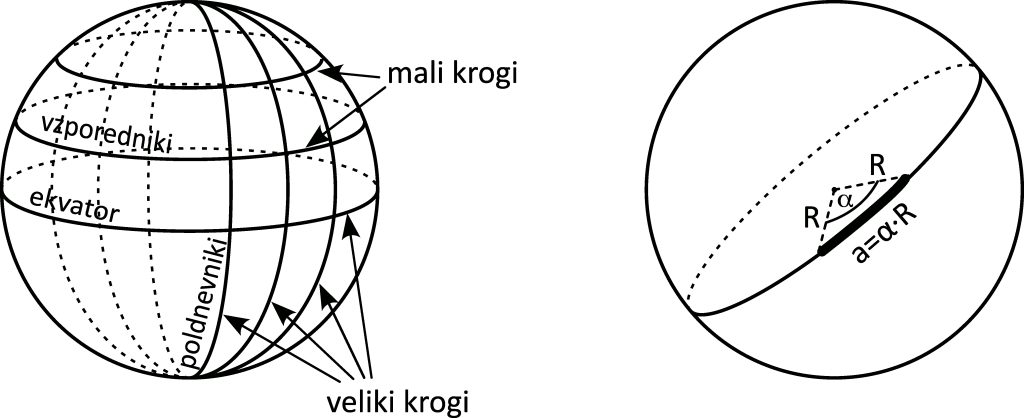
Veliki ali glavni krogi nam bodo pomagali opisati položaj točke na krogli. A še prej razmislimo, kako opisati razdaljo med dvema točkama na krogli (slika 2.3 desno). Vzemimo veliki krog, ki gre skozi obe točki. Središčni kot, ki ga točki oklepata, naj bo ![]() , polmer krogle naj bo
, polmer krogle naj bo ![]() . V tem primeru je najkrajša razdalja med točkama na površju krogle oziroma dolžina loka enaka
. V tem primeru je najkrajša razdalja med točkama na površju krogle oziroma dolžina loka enaka ![]() . Razdalja med točkama je torej določena s središčnim kotom. Sedaj moramo samo še izbrati vrednost za
. Razdalja med točkama je torej določena s središčnim kotom. Sedaj moramo samo še izbrati vrednost za ![]() — ker je nebesna krogla zelo velika in ker bi bilo nesmiselno meriti razdalje na nebu v enotah, kot so metri, izberemo kar
— ker je nebesna krogla zelo velika in ker bi bilo nesmiselno meriti razdalje na nebu v enotah, kot so metri, izberemo kar ![]() . Razdalje na nebu tako izražamo s kotom. Na primer, na Zemlji je razdalja med severnim polom in ekvatorjem enaka 90
. Razdalje na nebu tako izražamo s kotom. Na primer, na Zemlji je razdalja med severnim polom in ekvatorjem enaka 90![]() .
.
Preden definiramo koordinate na nebesni krogli, poglejmo bolj domače koordinate na zemeljski krogli.
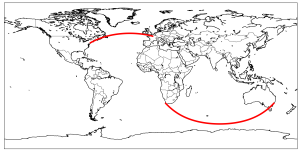
Najkrajšo razdaljo med dvema točkama na krogli dobimo, če ju povežemo z lokom velikega kroga. Zemlja je okrogla, zato na 2D projekciji, ki se uporablja največ (t. i. Mercatorjevi projekciji), najkrajša razdalja med dvema mestoma ni ravna črta. Na spodnjem zemljevidu rdeči krivulji označujeta najkrajši razdalji med Parizom in New Yorkom in med Cape Townom in Sydneyjem. Zemljevid je bil narisan z orodjem Basemap.
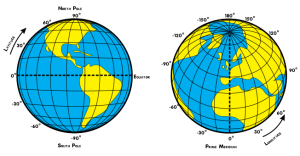
Koordinatni sistem na Zemlji
Vsak položaj na Zemlji opišemo z dvema koordinatama: zemljepisno širino ![]() in zemljepisno dolžino
in zemljepisno dolžino ![]() . Včasih je podana tudi nadmorska višina, a ta za določitev mesta na zemeljskem površju ni potrebna. Tukaj privzamemo, da je Zemlja popolna matematična krogla.
. Včasih je podana tudi nadmorska višina, a ta za določitev mesta na zemeljskem površju ni potrebna. Tukaj privzamemo, da je Zemlja popolna matematična krogla.
Zemljepisna širina in dolžina sta razdalji od nekega izbranega velikega kroga. Vprašanje je, kateri krog izberemo za izhodišče. V primeru zemljepisne širine se odgovor ponuja kar sam: Zemljin ekvator (slika 2.5). Ekvator je veliki krog, pravokoten na os vrtenja Zemlje. Mali krogi, ki so ekvatorju vzporedni, so vzporedniki. Točki, kjer os vrtenja prebada Zemljino kroglo — kjer mali krog oziroma vzporednik postane točka — imenujemo Zemljin severni in južni pol.
Sedaj poglejmo družino velikih krogov, ki gredo skozi pola. Te kroge imanujemo poldnevniki, saj povezujejo kraje na Zemlji, ki imajo poldne ob istem času. Zemljepisna širina je razdalja od ekvatorja in je merjena vzdolž poldnevnika. Njene vrednosti so lahko med ![]() in
in ![]() , pri čemer je zemljepisna širina negativna na južni in pozitivna na severni polobli.
, pri čemer je zemljepisna širina negativna na južni in pozitivna na severni polobli.
Zemljepisna dolžina je razdalja vzdolž ekvatorja od izbranega ničelnega poldnevnika (poldnevnika z zemljepisno dolžino 0![]() ). V nasprotju z ekvatorjem ni naravnega ničelnega poldnevnika — vsi poldnevniki so enakovredni. Iz zgodovinskih razlogov za ničelni poldnevnik velja poldnevnik, ki poteka skozi Kraljevi observatorij Greenwich v Londonu. Dolžino merimo od vrednosti 0
). V nasprotju z ekvatorjem ni naravnega ničelnega poldnevnika — vsi poldnevniki so enakovredni. Iz zgodovinskih razlogov za ničelni poldnevnik velja poldnevnik, ki poteka skozi Kraljevi observatorij Greenwich v Londonu. Dolžino merimo od vrednosti 0![]() do 360
do 360![]() , pri čemer dolžina narašča proti vzhodu. Večkrat se uporablja tudi zapis vzhodno ali zahodno od Greenwicha, pri čemer so vrednosti dolžine med
, pri čemer dolžina narašča proti vzhodu. Večkrat se uporablja tudi zapis vzhodno ali zahodno od Greenwicha, pri čemer so vrednosti dolžine med ![]() in
in ![]() .
.
Kot primer poglejmo Zelo velik teleskop (ang. Very Large Telescope) Evropskega južnega observatorija, ki stoji v Čilu. Zemljepisna širina observatorija je ![]()
![]()
![]() , kar bi lahko zapisali tudi kot
, kar bi lahko zapisali tudi kot ![]()
![]()
![]() S, pri čemer S označuje jug (ang. South), saj je observatorij južno od ekvatorja. Zemljepisna dolžina observatorija je
S, pri čemer S označuje jug (ang. South), saj je observatorij južno od ekvatorja. Zemljepisna dolžina observatorija je ![]()
![]()
![]() , kar bi lahko zapisali tudi kot
, kar bi lahko zapisali tudi kot ![]()
![]()
![]() W, pri čemer W označuje zahod (ang. West), saj je observatorij zahodno od Greenwicha. Ekvivalentno bi lahko dolžino zapisali tudi kot
W, pri čemer W označuje zahod (ang. West), saj je observatorij zahodno od Greenwicha. Ekvivalentno bi lahko dolžino zapisali tudi kot ![]()
![]()
![]() Včasih se zemljepisna širina in dolžina podajata tudi v decimalkah stopinje. V decimalnem zapisu sta zemljepisna širina in dolžina observatorija približno
Včasih se zemljepisna širina in dolžina podajata tudi v decimalkah stopinje. V decimalnem zapisu sta zemljepisna širina in dolžina observatorija približno ![]() in
in ![]() .
.
Koordinatni sistem na Zemlji oziroma geografski koordinatni sistem nam pomaga razumeti koordinatni sistem na nebesni krogli. Koordinate na Zemlji so v astronomiji pomembne tudi same po sebi. Od položaja na Zemlji je namreč odvisno, kako je videti nočno nebo v določenem trenutku.
Horizontni koordinatni sistem
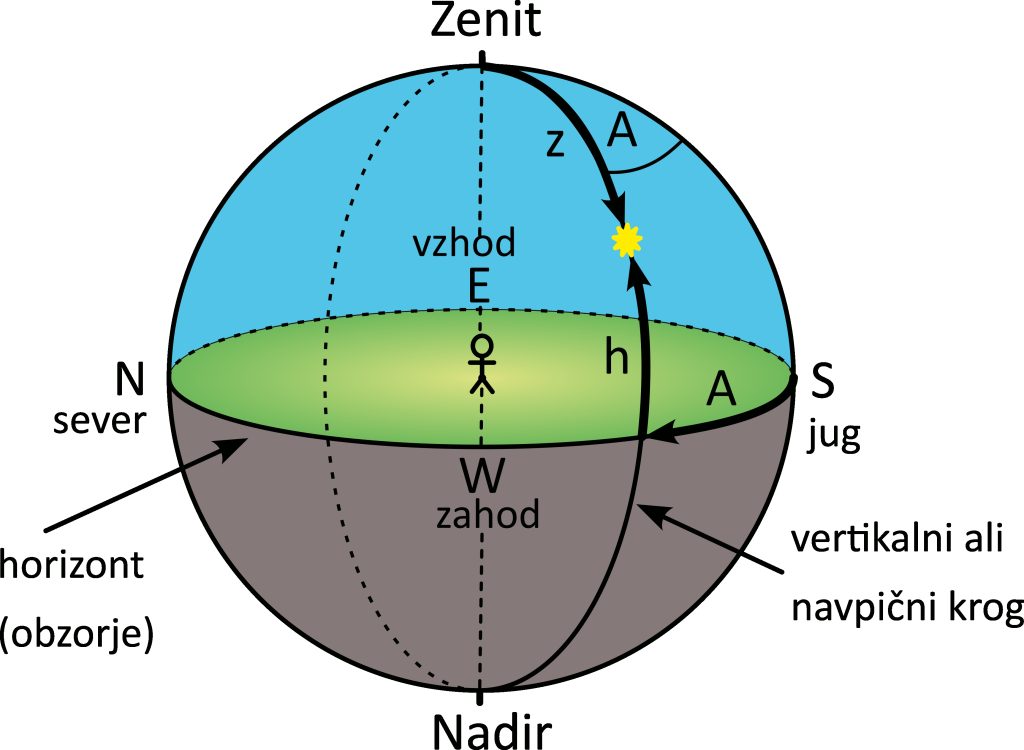
Ko se pripravljamo na astronomsko opazovanje z neke točke na Zemljinem površju (opazovališča), nas zanima, kako je videti nebo s te lokacije. Predpostavimo, da našega pogleda ne ovirajo gore, stavbe ali drevesa — da vidimo nebo, kot da smo na otoku sredi oceana. Nad nami se boči polovica nebesne krogle, medtem ko je druga polovica skrita pod tlemi. Obe polovici loči obzorje oziroma horizont (slika 2.6). Matematično gledano je horizont veliki krog.
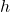 (ali zenitno razdaljo
(ali zenitno razdaljo  ) in azimutom
) in azimutom 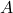 .
.Ozrimo se navpično navzgor. Točko na nebesni krogli točno nad nami imenujemo zenit (tudi nadglavišče). Sedaj se ozrimo navzdol — točko točno pod nami imenujemo nadir (tudi podnožišče). Za orientacijo na horizontu označimo smeri neba, pri čemer običajno uporabljamo angleško notacijo (N za sever, S za jug, E za vzhod in W za zahod).
Postavili smo ogrodje horizontnega koordinatnega sistema. Ta sistem je odvisen od opazovališča (slika 2.7) in ni fiksiran na zvezde, zato se zaradi vrtenja in gibanja Zemlje koordinate zvezd v njem s časom spreminjajo. Ne samo to, položaj iste zvezde je v istem trenutku za opazovalce in opazovalke na različnih krajih Zemlje različen. S katerima koordinatama pa bi v tem sistemu lahko opisali položaj točke (zvezde ali drugega telesa) na nebu?
Znova poglejmo sliko 2.6. Nebesno kroglo presekamo z ravnino, na kateri ležita zveznica nadir–zenit in telo. Dobimo veliki krog, ki gre skozi zenit, telo in nadir. Naša prva koordinata bo višina ![]() , to je lok vzdolž tega velikega kroga, od horizonta do telesa. Večkrat srečamo tudi kot med zenitom in telesom, ki mu pravimo zenitna razdalja. Iz slike preberemo, da za višino in zenitno razdaljo nekega telesa vedno velja
, to je lok vzdolž tega velikega kroga, od horizonta do telesa. Večkrat srečamo tudi kot med zenitom in telesom, ki mu pravimo zenitna razdalja. Iz slike preberemo, da za višino in zenitno razdaljo nekega telesa vedno velja ![]() +
+ ![]() .
.
Višina in zenitna razdalja
Kolikšne vrednosti lahko zavzameta višina ![]() in zenitna razdalja
in zenitna razdalja ![]() ? Kolikšne so zenitne razdalje teles v zenitu, na obzorju in v nadiru?
? Kolikšne so zenitne razdalje teles v zenitu, na obzorju in v nadiru?
V astronomiji je pomemben poseben veliki krog, ki gre skozi zenit, točko točno na jugu obzorja in nadir. Nebesna telesa so v svojem dnevnem navideznem gibanju namreč najviše na nebu ravno takrat, ko prečkajo ta krog. Imenujemo ga krajevni nebesni poldnevnik ali nebesni meridian opazovališča. Nebesni meridian je pravzaprav podaljšek ali projekcija krajevnega poldnevnika na Zemlji na nebesno sfero.
Nebesni meridian nam bo služil kot referenca za merjenje druge koordinate horizontnega sistema. Dolžina loka vzdolž horizonta med nebesnim meridianom in točko, kjer veliki krog skozi telo seka horizont, imenujemo azimut ![]() [1] (glej sliko 2.6). Po dogovoru imajo položaji zahodno od nebesnega meridiana azimut med 0 in
[1] (glej sliko 2.6). Po dogovoru imajo položaji zahodno od nebesnega meridiana azimut med 0 in ![]() , položaji vzhodno od nebesnega meridiana med 0 in
, položaji vzhodno od nebesnega meridiana med 0 in ![]() .
.
Horizontni koordinatni sistem je uporaben za ugotavljanje časa vzhoda in zahoda nebesnih teles. Če je azimut pozitiven (ali med 0 in ![]() ), potem telo zahaja, če je negativen (ali med 180 in
), potem telo zahaja, če je negativen (ali med 180 in ![]() ), telo vzhaja.
), telo vzhaja.
Interaktivno
Horizontni koordinatni sistem je odvisen od opazovališča na Zemlji. Odvisnost raziščite s pomočjo simulacije.
Koordinati v horizontnem sistemu sta višina ![]() in azimut
in azimut ![]() . Za boljše razumevanje teh dveh koordinat poskusite naslednjo simulacijo. Pozor: v tej simulaciji merijo azimut od severa.
. Za boljše razumevanje teh dveh koordinat poskusite naslednjo simulacijo. Pozor: v tej simulaciji merijo azimut od severa.
Ekvatorski koordinatni sistem
Horizontni koordinatni sistem je odvisen od opazovališča, zato za številne namene ni najbolj primeren (na primer, če želimo opazovati isto nebesno telo z dveh opazovališč). Poleg tega se koordinati nebesnih teles v njem spreminjajo s časom. Sistem, neodvisen od opazovališča in od časa, je ekvatorski koordinatni sistem. V tem sistemu središče nebesne krogle postavimo v središče Zemlje.
Začnimo graditi ekvatorski sistem z osnovnim opažanjem, da se nebo vrti. Vrtenje je navidezno, saj se v resnici vrti Zemlja; Zemlja se vrti od zahoda proti vzhodu, zato se nebo navidezno vrti v nasprotni smeri, od vzhoda proti zahodu, os vrtenja pa je ista, kot je Zemljina os vrtenja (slika 1.1). Presečišči podaljšane osi vrtenja Zemlje in nebesne krogle sta severni nebesni pol (ki je zelo blizu zvezde Severnice) in južni nebesni pol (v bližini južnega nebesnega pola ni nobene svetle zvezde). Z opazovališč na Zemljini severni polobli vidimo, da zvezde navidezno krožijo okoli severnega pola, z opazovališč na Zemljini južni polobli, da navidezno krožijo okoli južnega nebesnega pola.
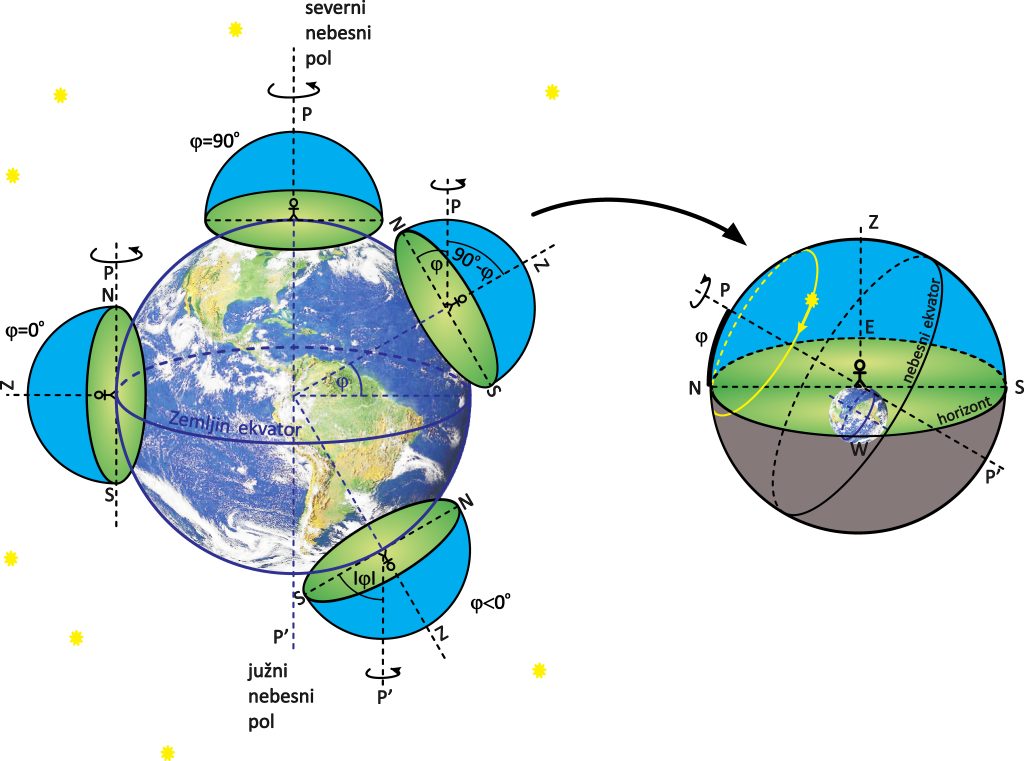
Na sliki 2.7 vidimo različna opazovališča. V opazovališču na Zemljinem severnem polu (zemljepisna širina ![]() ) je severni nebesni pol v zenitu, njegova višina je torej
) je severni nebesni pol v zenitu, njegova višina je torej ![]() . Višina severnega pola nad obzorjem je enaka zemljepisni širini tega opazovališča. V opazovališču na Zemljinem ekvatorju (
. Višina severnega pola nad obzorjem je enaka zemljepisni širini tega opazovališča. V opazovališču na Zemljinem ekvatorju (![]() ) sta oba nebesna pola na obzorju, njuna višina je
) sta oba nebesna pola na obzorju, njuna višina je ![]() . V opazovališču na severni zemljepisni širini
. V opazovališču na severni zemljepisni širini ![]() je višina severnega pola nad obzorjem enaka
je višina severnega pola nad obzorjem enaka ![]() . V opazovališču na južni zemljepisni širini
. V opazovališču na južni zemljepisni širini ![]() je višina južnega pola nad obzorjem enaka
je višina južnega pola nad obzorjem enaka ![]() .
.
Nebesna krogla se vrti okoli zveznice severnega in južnega nebesnega pola. Presek nebesne krogle z ravnino skozi njeno središče in pravokotno na zveznico polov (na os vrtenja) ustvari veliki krog: nebesni ekvator. Nebesni ekvator je pravzaprav podaljšek ali projekcija Zemljinega ekvatorja na nebesno kroglo.
Interaktivno
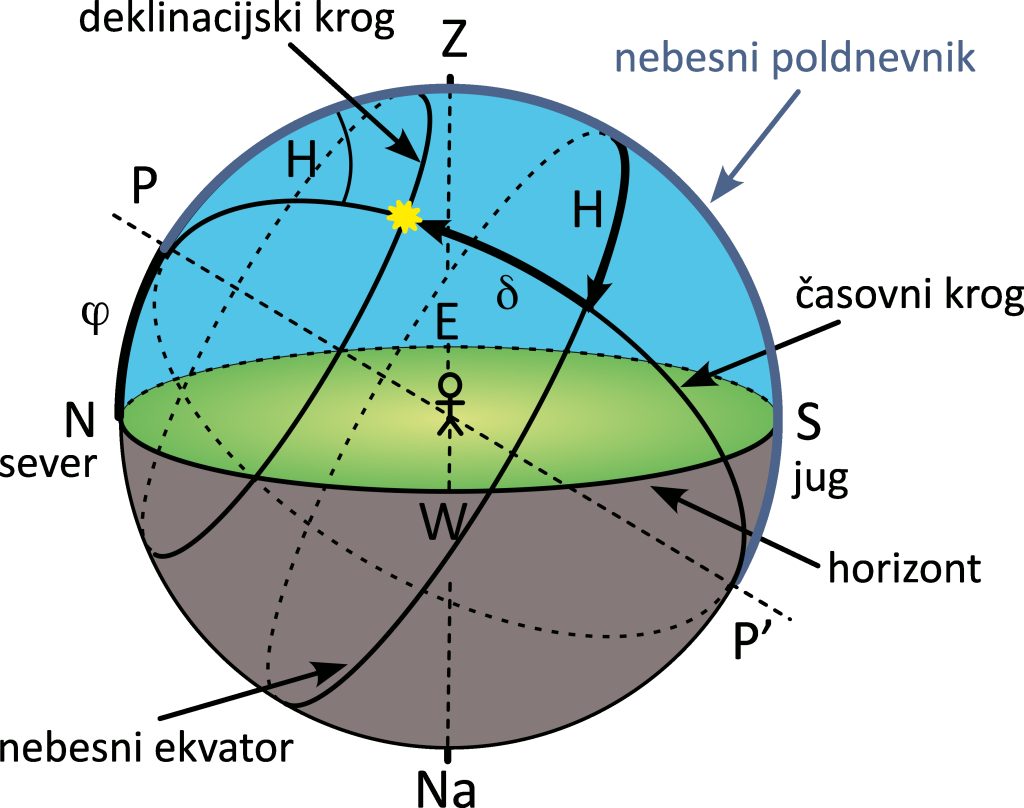
Ekvatorski koordinatni sistem spoznajmo podrobneje s sliko 2.8. Zvezda se skupaj z nebesno kroglo vrti okoli zveznice med nebesnima poloma; v enem vrtljaju opiše mali krog na krogli, ki je vzporeden nebesnemu ekvatorju in mu pravimo deklinacijski krog. Opisani krog spominja na Zemljine vzporednike. Zato uvedemo koordinato, ki je podobna zemljepisni širini. Kotni razdalji med nebesnim ekvatorjem in tem krogom, po katerem se giblje zvezda, merjeni vzdolž velikega kroga, ki poteka skozi nebesna pola in zvezdo, pravimo deklinacija. Označimo jo z grško črko ![]() (ponekod jo označujejo z dec, iz angleškega izraza declination). Deklinacija je neodvisna od opazovališča in od časa.
(ponekod jo označujejo z dec, iz angleškega izraza declination). Deklinacija je neodvisna od opazovališča in od časa.
Kolikšne vrednosti lahko zavzame deklinacija? Brez kukanja po katalogih ocenite, kolikšna je deklinacija zvezde Severnice.
Drugo koordinato bomo dobili v dveh korakih. Analogno azimutu pri horizontnem sistemu tukaj vpeljemo koordinato, ki meri kotno razdaljo med nebesnim poldnevnikom in presečiščem nebesnega ekvatorja in velikega kroga, ki gre skozi nebesna pola in zvezdo (slika 2.8) in mu pravimo časovni krog. Tej razdalji pravimo časovni kot ![]() , ker se enakomerno povečuje s časom (saj sledi vrtenju nebesne krogle oziroma vrtenju Zemlje). Vrednosti časovnega kota gredo od 0 do
, ker se enakomerno povečuje s časom (saj sledi vrtenju nebesne krogle oziroma vrtenju Zemlje). Vrednosti časovnega kota gredo od 0 do ![]() v 24 urah, kar pomeni, da se vsako uro poveča za
v 24 urah, kar pomeni, da se vsako uro poveča za ![]() , zato ga pogosto izražamo kar v urah (po pretvorbi, da je 1
, zato ga pogosto izražamo kar v urah (po pretvorbi, da je 1![]() enaka
enaka ![]() ). Običajno vrednosti časovnega kota podajamo na intervalu
). Običajno vrednosti časovnega kota podajamo na intervalu ![]() do
do ![]() ali
ali ![]() do
do ![]() .
.
Časovni kot je odvisen od opazovališča in časa, mi pa potrebujemo koordinato, ki bo od opazovališča in časa neodvisna. Zagato so rešili z dogovorom, da kota ne merimo od lokalnega nebesnega poldnevnika, temveč od določene točke na nebesnem ekvatorju, ki je ista za vsa opazovališča in ob vseh časih. Kot referenca je bila izbrana točka na nebesnem ekvatorju, kjer je Sonce ob pomladanskem enakonočju. Ta točka se imenuje pomladišče in jo označimo z grško črko ![]() (slika 2.9). Naša prava, od opazovališča neodvisna koordinata, je lok vzdolž nebesnega ekvatorja med pomladiščem in presečiščem nebesnega ekvatorja in časovnega kroga. To koordinato imenujemo rektascenzija in jo običajno označujemo z grško črko
(slika 2.9). Naša prava, od opazovališča neodvisna koordinata, je lok vzdolž nebesnega ekvatorja med pomladiščem in presečiščem nebesnega ekvatorja in časovnega kroga. To koordinato imenujemo rektascenzija in jo običajno označujemo z grško črko ![]() (v nekaterih angleških virih jo označujejo z R.A., kar izhaja iz angleškega izraza zanjo — right ascension).
(v nekaterih angleških virih jo označujejo z R.A., kar izhaja iz angleškega izraza zanjo — right ascension).
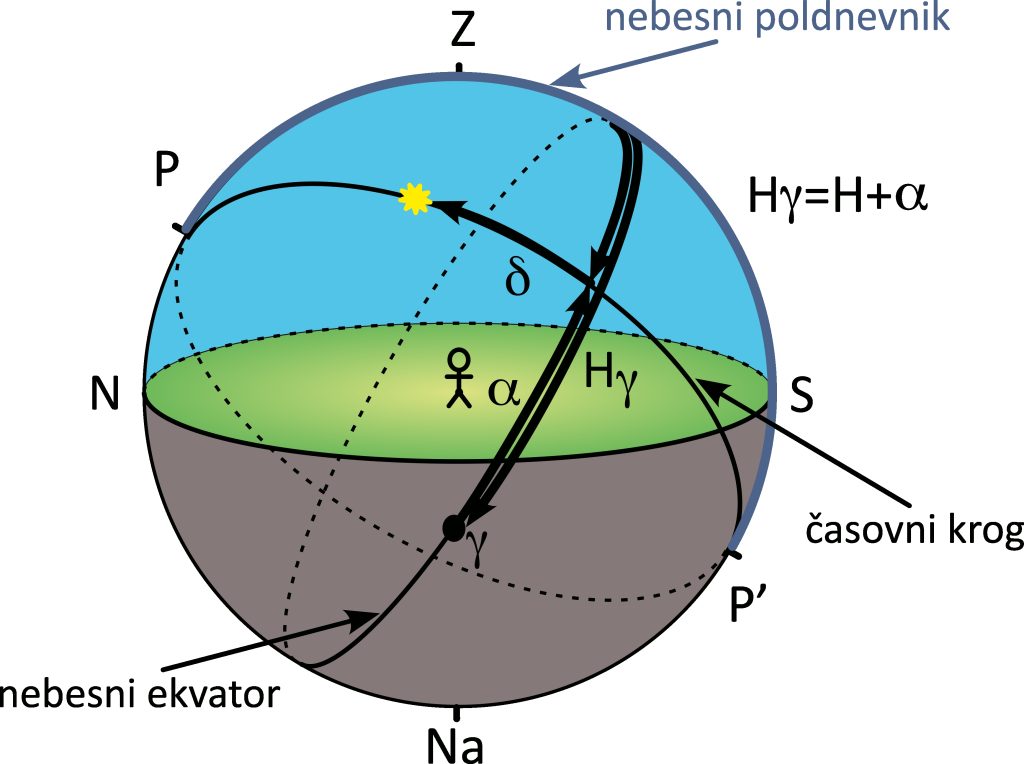
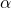 merimo od pomladišča
merimo od pomladišča 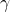 .
.
Rektascenzija in deklinacija sta torej koordinati, neodvisni od opazovališča in od časa. V katalogih zvezd in drugih nebesnih teles so njihovi položaji podani z vrednostmi rektascenzije in deklinacije. Za opazovanje s prostim očesom ali ročno vodenim teleskopom sta ti dve koordinati manj praktični od koordinat horizontnega koordinatnega sistema. Pri opazovanju z računalniško vodenim teleskopom pa sta nadvse uporabni.
Koordinatni mreži na nebu
Tako bi bil videti ekvatorski koordinatni sistem na nebu (če bi na njem narisali kroge s konstantnimi deklinacijami in rektascenzijami). Mreža izhaja iz severnega nebesnega pola, ki je zelo blizu Severnice. Krogi označujejo položaje na nebu z isto deklinacijo, črte položaje z isto rektascenzijo. Mreža je narisana s programom Stellarium. Odprite program in tudi vi narišite mrežo nad vašim nebom. Na zaslon dodajte še azimutni koordinatni sistem. Poglejte, kako se s časom spreminja položaj zvezd glede na oba koordinatna sistema.
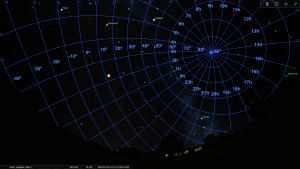
Interaktivno
Merjenje časa
Časovni koti nebesnih teles se spreminjajo premo sorazmerno s časom, zato jih lahko uporabimo za merjenje lokalnega časa. Po dogovoru je krajevni zvezdni čas (tudi siderski čas) časovni kot pomladišča:
(1) ![]()
Kot je razvidno iz zgornje slike, za vsako nebesno telo ob vsakem času velja:
(2) ![]()
Dnevno gibanje nebesnih teles
Poglejmo, kako v horizontnem in ekvatorskem koordinatnem sistemu opišemo gibanje zvezd na nebu zaradi vrtenja Zemlje — v času enega dneva (24 ur). Omejimo se na opazovališča na severni polobli, pri čemer si pomagamo s horizontnim in ekvatorskim sistemom, opisanima zgoraj, in s sliko 2.11. Telo je na nebu najviše, ko prečka nebesni poldnevnik. Takrat je telo v zgornji kulminaciji. Ker je telo na nebesnem poldnevniku, je njegov časovni kot ![]() . Iz enačbe 2 sledi, da je
. Iz enačbe 2 sledi, da je ![]() : telo kulminira, ko je krajevni zvezdni čas enak njegovi rektascenziji. Zvezde v zgornji kulminaciji so zato primerne za merjenje časa in, kot bomo videli kmalu, položaja na Zemlji, torej dober pripomoček za navigacijo.
: telo kulminira, ko je krajevni zvezdni čas enak njegovi rektascenziji. Zvezde v zgornji kulminaciji so zato primerne za merjenje časa in, kot bomo videli kmalu, položaja na Zemlji, torej dober pripomoček za navigacijo.
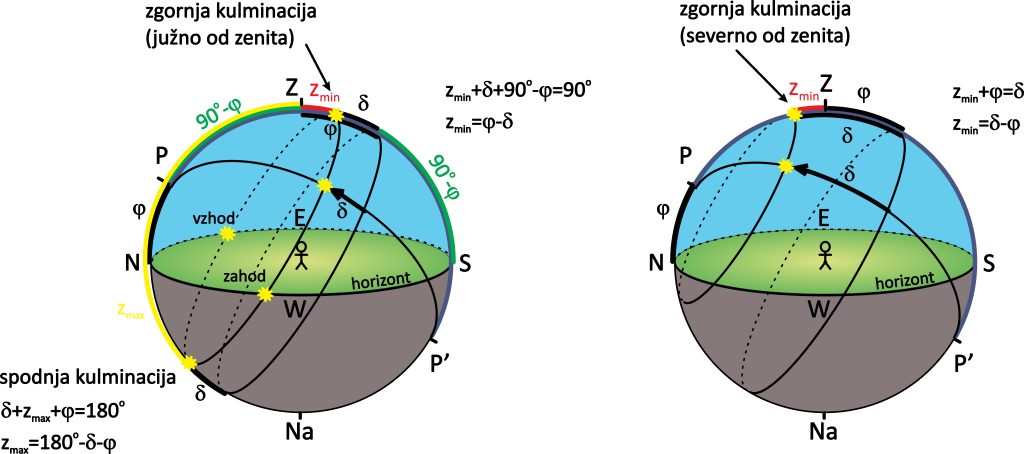
Skici na sliki 2.11 prikazujeta dva primera zgornje kulminacije zvezde glede na zenit — zvezda kulminira južno ali severno od zenita, kar je odvisno od deklinacije zvezde ![]() in zemljepisne širine
in zemljepisne širine ![]() opazovališča:
opazovališča:
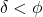 . Zvezda kulminira južno od zenita in ob kulminaciji velja:
. Zvezda kulminira južno od zenita in ob kulminaciji velja: 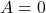 ,
, 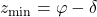 ,
, 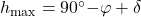 .
.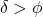 . Zvezda kulminira severno od zenita in ob kulminaciji velja:
. Zvezda kulminira severno od zenita in ob kulminaciji velja: 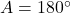 ,
, 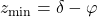 ,
, 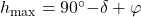 .
.
Podobzornice, nadobzornice, vzhajalke
Telo je najvišje na nebu ob zgornji kulminaciji, ko prečka nebesni meridian (smer proti jugu). Takrat je ![]() in
in ![]() . Najnižje na nebu je v smeri severa ob spodnji kulminaciji, ko je
. Najnižje na nebu je v smeri severa ob spodnji kulminaciji, ko je ![]() . Takrat je
. Takrat je ![]() , zenitna razdalja je največja:
, zenitna razdalja je največja: ![]() . Njegova višina nad obzorjem je
. Njegova višina nad obzorjem je ![]() , njen predznak pove ali je telo takrat nad obzorjem (
, njen predznak pove ali je telo takrat nad obzorjem (![]() ), na obzorju (
), na obzorju (![]() ) ali pod obzorjem (
) ali pod obzorjem (![]() ).
).
Za opazovališče z zemljepisno širino ![]() imamo zvezde, ki so:
imamo zvezde, ki so:
- podobzornice – zvezde, ki v tem opazovališču nikoli ne vzidejo;
- nadobzornice ali cirkumpolarne zvezde – zvezde, ki nikoli ne zaidejo;
- vzhajalke – zvezde, ki vzidejo in zaidejo.
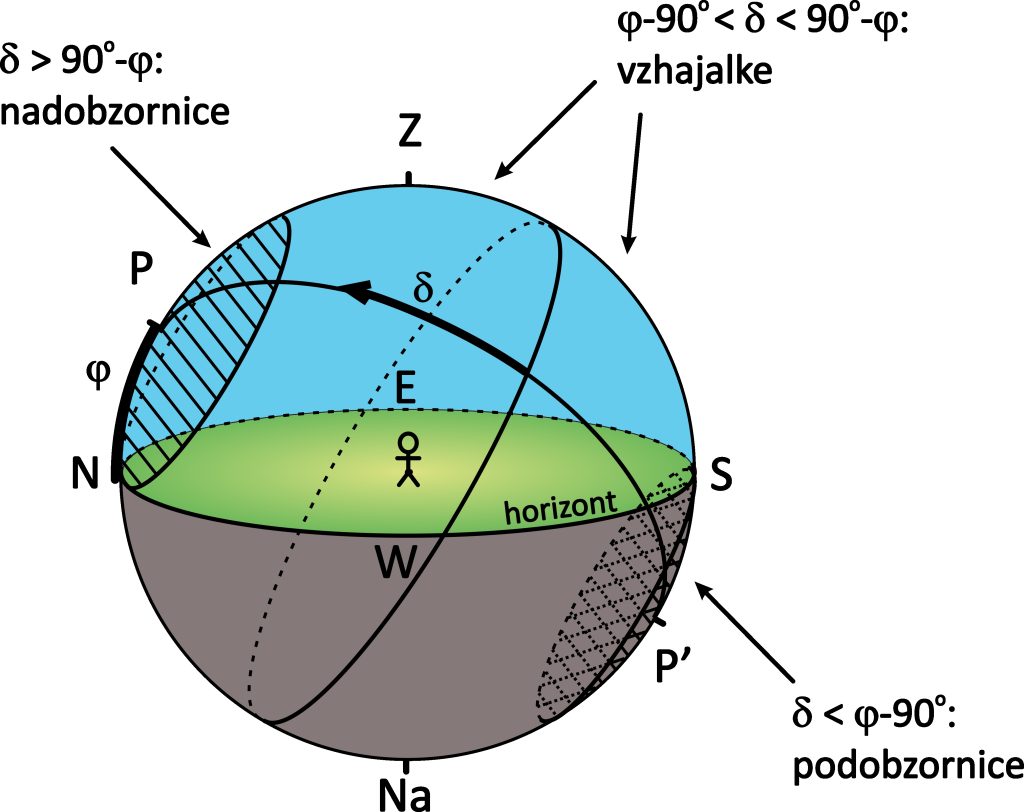
Kakšna mora biti deklinacija zvezde ![]() (izražena z
(izražena z ![]() ), da je v kraju z zemljepisno širino
), da je v kraju z zemljepisno širino ![]() podobzornica, nadobzornica ali vzhajalka? V pomoč je naslednja ilustracija.
podobzornica, nadobzornica ali vzhajalka? V pomoč je naslednja ilustracija.
Odgovor
- podobzornica:
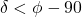 ,
, - nadobzornica:
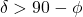 ,
, - vzhajalka:
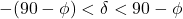
Letno spreminjanje neba
Katere zvezde so vidne na nočnem nebu, je odvisno od položaja Zemlje glede na Sonce (slika 2.13). Sonce oddaja veliko svetlobe, ki se siplje na molekulah in delcih Zemljinega ozračja. Posledično je čez dan nebo tako svetlo, da šibkih nebesnih teles na njem ne vidimo. Zato zvezd, ki so nad obzorjem podnevi, ne vidimo. Vidimo le tiste zvezde, ki so nad obzorjem opazovališča ponoči.
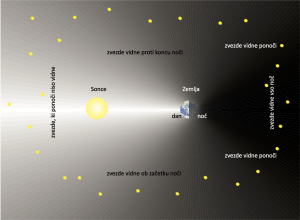
Z gibanjem Zemlje okoli Sonca se spreminja smer proti Soncu, kar je posledica razlike med vrtilno dobo Zemlje glede na oddaljene zvezde in glede na Sonce (več o tem v poglavju Sonce in merjenje časa). S tem se menjajo tudi zvezde, ki so na nebu v Sončevi bližini (a so v resnici daleč za njim, slika 2.14). Teh zvezd v tem delu leta na nočnem nebu ne vidimo, saj so nad obzorjem podnevi (tako kot Sonce). Tako pri nas v zimskih mesecih lahko občudujemo ozvezdje Orion, v poletnih mesecih ozvezdje Škorpijon. Ozvezdja, ki so na nebu daleč od ravnine, po kateri se navidezno giblje Sonce (imenovane ekliptika), so vidna skozi vse leto, na primer, Veliki Medved.

Interaktivno
*Trikotniki na sferi
Če pozorno pogledamo zgornje skice, opazimo, da sekanje velikih krogov na sferi vodi do sfernih trikotnikov. Ti trikotniki so uporabni, saj tako kot za navadne, ravninske trikotnike zanje veljata kosinusni in sinusni izrek, le da sta nekoliko drugačna.
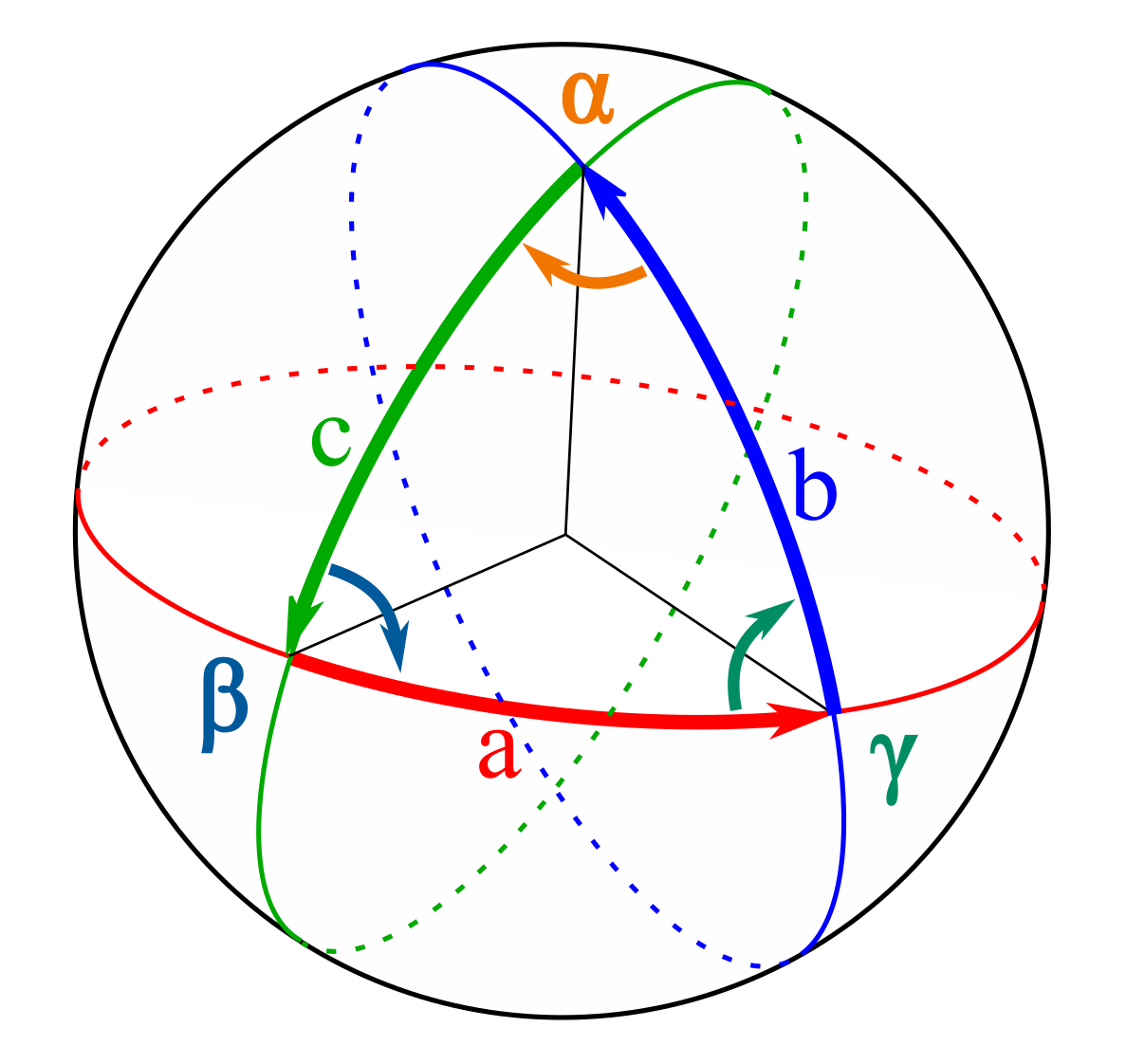
Sferni trikotnik opisujejo tri oglišča ![]() in
in ![]() , njim nasproti ležeče stranice
, njim nasproti ležeče stranice ![]() in
in ![]() , ki so loki glavnih krogov, in koti med stranicami
, ki so loki glavnih krogov, in koti med stranicami ![]() in
in ![]() . Tako koti kot stranice naj so manjši ali kvečjemu enaki
. Tako koti kot stranice naj so manjši ali kvečjemu enaki ![]() . V nasprotju z ravninskim trikotnikom je vsota vseh kotov sfernega trikotnika
. V nasprotju z ravninskim trikotnikom je vsota vseh kotov sfernega trikotnika ![]() .
.
Kosinusni izrek povezuje dolžino ene stranice z dolžinama drugih dveh stranic in kotom med njima. Za sferni trikotnik je kosinusni izrek:
(3) 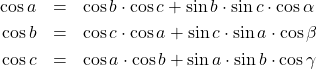
Sinusni izrek povezuje kote in njim nasproti ležeče stranice. Za sferni trikotnik je sinusni izrek:
(4) ![]()
Za trikotnike na nebesni sferi lahko iz znanih vrednosti določenih kotov in stranic z uporabo kosinusnega in sinusnega izreka izračunamo neznane kote in stranice.
Omenili smo, da najkrajša razdalja med dvema točkama na Zemlji poteka vzdolž velikega kroga. Recimo, da letalo želi poleteti iz Madrida (![]() W,
W, ![]() N) v New York (
N) v New York (![]() W,
W, ![]() N). Privzemimo, da je Zemlja popolna krogla s polmerom
N). Privzemimo, da je Zemlja popolna krogla s polmerom ![]() km.
km.
1. Kolikšna je najkrajša razdalja med tema mestoma? Pomagajte si s skico in z uporabo kosinusnega izreka za sferni trikotnik.
Odgovor
51.9![]() oziroma 5800 km
oziroma 5800 km
2. Mesti ležita skoraj na isti zemljepisni širini. Privzemimo, da ležita na isti širini. Kolikšna je v tem primeru razdalja med njima, merjena vzdolž vzporednika?
Odgovor
5960 km
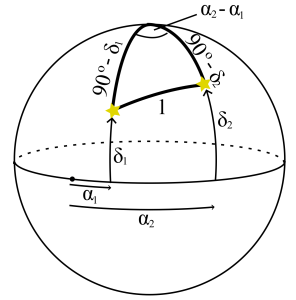
Pogosto nas zanima, kolikšna je kotna razdalja ![]() med dvema telesoma na nebu. Prvo telo naj ima koordinate
med dvema telesoma na nebu. Prvo telo naj ima koordinate ![]() in
in ![]() , drugo
, drugo ![]() in
in ![]() . Uporabimo kosinusni izrek in dobimo
. Uporabimo kosinusni izrek in dobimo
(5) ![]()
Upoštevamo, da velja ![]() in
in ![]() . Enačba se skrajša v
. Enačba se skrajša v
(6) ![]()
V primeru majhnih razdalj je možno izraz še dodatno poenostaviti. V tem primeru zapišemo koordinate kot ![]() in
in ![]() , kjer sta
, kjer sta ![]() in
in ![]() majhni spremembi. Vstavimo v enačbo 6. Upoštevamo, da za majhne kote
majhni spremembi. Vstavimo v enačbo 6. Upoštevamo, da za majhne kote ![]() velja
velja ![]() in
in ![]() in dobimo enačbo:
in dobimo enačbo:
(7) ![]()
kjer je ![]() . Enačbo si je lahko zapomniti, saj spominja na Pitagorov izrek (z manjšim dodatkom).
. Enačbo si je lahko zapomniti, saj spominja na Pitagorov izrek (z manjšim dodatkom).
- V nekateri literaturi se azimut meri od severa, zato pazljivo. ↵
