Sonce in merjenje časa

Jure Japelj; Andreja Gomboc

3 Sonce in merjenje časa

Jure Japelj and Andreja Gomboc

V prejšnjem poglavju in na sliki 2.14 smo spoznali, da je podoba zvezdnega neba odvisna od položaja oziroma gibanja Zemlje glede na Sonce. Od tega je odvisno tudi navidezno gibanje Sonca na nebu.

Vrtenje Zemlje okoli osi ima na navidezno gibanje Sonca enak vpliv kot na zvezde. Sonce navidezno kroži okoli nebesnega pola. Ko se mu na določenem opazovališču zenitna razdalja zmanjša pod $90\degr$ , vzide na vzhodnem delu neba. Najvišjo točko doseže na nebesnem poldnevniku, začne zahajati in zaide na zahodnem delu neba. A skozi leto postane pot Sonca po nebu bolj zapletena od navideznega gibanja zvezd, ker se Zemlja giblje okoli Sonca. Poglejmo podrobneje.

Letno gibanje Sonca

Ravnino, po kateri se Zemlja giblje okoli Sonca, imenujemo ekliptična ravnina. Nagnjena je za $\varepsilon=23\degr27\arcmin$ glede na Zemljin ekvator (lahko rečemo tudi, da je Zemljina os nagnjena za $\varepsilon=23\degr 27\arcmin$ glede na pravokotnico na ravnino gibanja Zemlje okoli Sonca, kar je ekvivalentna trditev). Gledano z Zemlje je videti, kot da se Sonce premika po tej ravnini, zato tudi pot Sonca po nebu glede na oddaljene zvezde imenujemo ekliptika^[1]. Koordinati Sonca v ekvatorskem koordinatnem sistemu, zapisali ju bomo kot $\alpha_{\odot}$ in $\delta_{\odot}$ , se skozi leto torej spreminjata.

Inklinacija planetov glede na ekliptiko

Ravnine tirnic planetov so malo nagnjene glede na ekliptično ravnino. Pravimo, da imajo tirnice od nič različno inklinacijo $i$ glede na ekliptično ravnino. Za večino planetov je ta kot le nekaj stopinj, kar ni nepričakovano, saj so planeti nastali iz protoplanetarnega diska. Inklinacija planetov je zapisana v spodnji tabeli. Ekliptična ravnina sama je za dobrih sedem stopinj nagnjena glede na ravnino Sončevega ekvatorja.

	Merkur	Venera	Zemlja	Mars	Jupiter	Saturn	Uran	Neptun
$i$	7.01 $\degr$	3.39 $\degr$	0 $\degr$	1.85 $\degr$	1.31 $\degr$	2.49 $\degr$	0.77 $\degr$	1.77 $\degr$

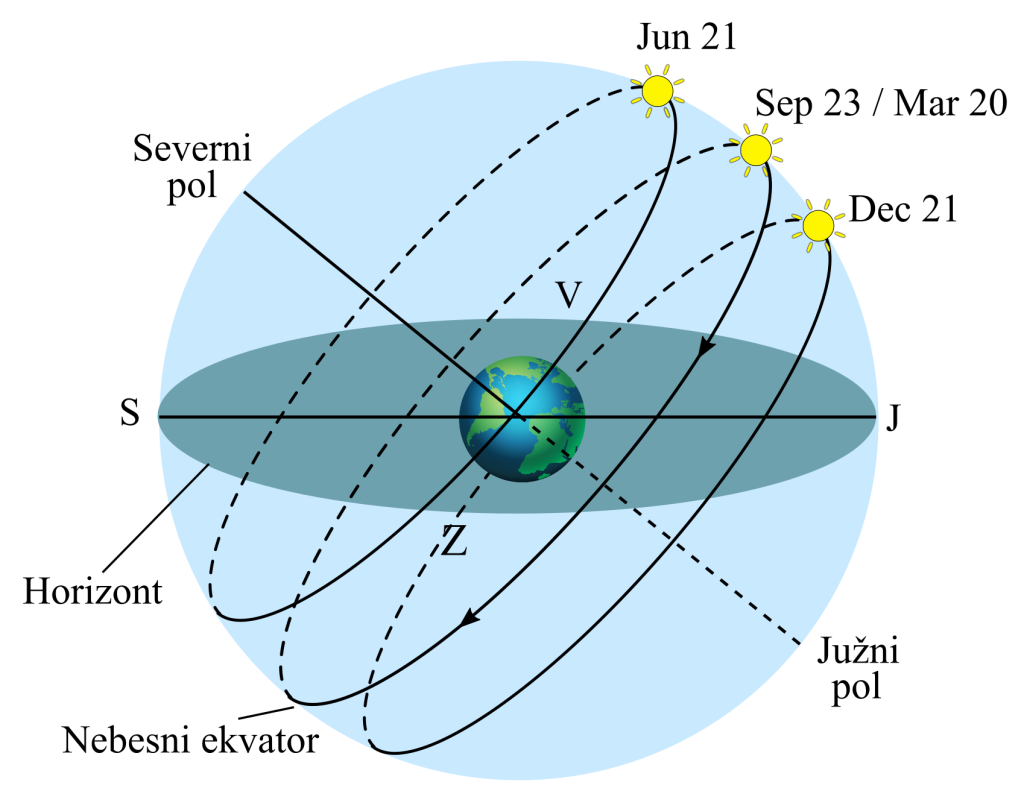
Spreminjanje rektascenzije in deklinacije Sonca lahko razumemo s pomočjo spodnje slike, kjer je ekliptika vrisana na nebesno kroglo.

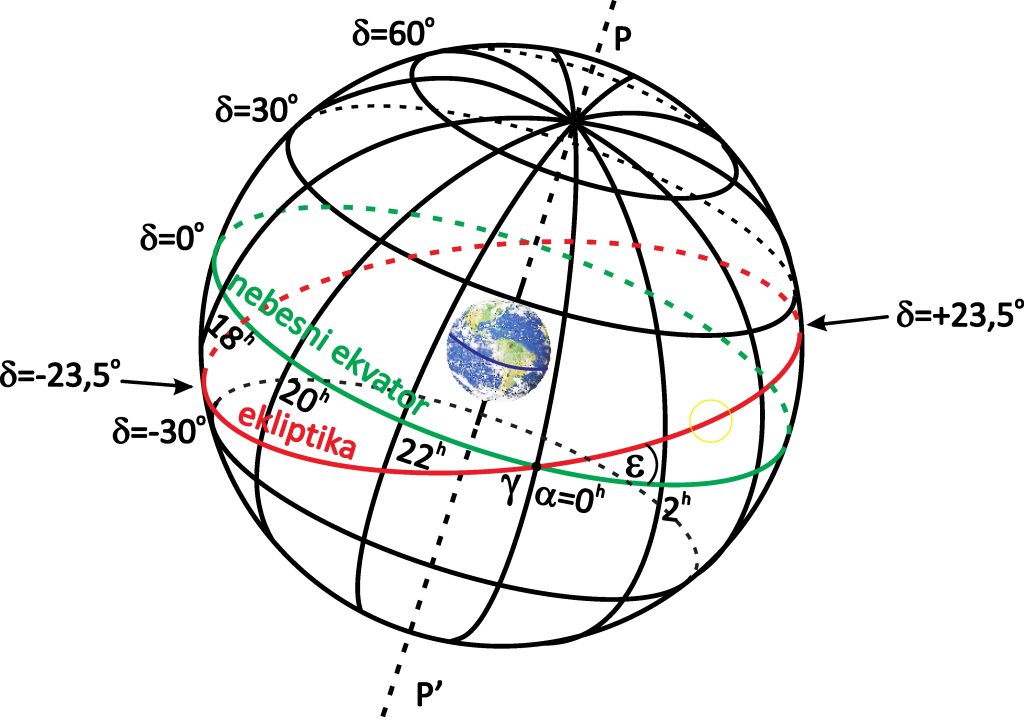
Slika 3.1: Ekliptika v ekvatorskem koordinatnem sistemu.

Spreminjanje rektascenzije in deklinacije Sonca lahko razumemo s pomočjo slike 3.1, kjer je ekliptika vrisana na nebesno kroglo. Rektascenzija med letom zavzame vrednosti med $0^{\rm h}$ in $24^{\rm h}$ , deklinacija med $-\varepsilon$ in $+\varepsilon$ ( $\varepsilon=23.5\degr$ ). S slike razberemo več informacij.

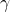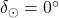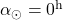Nebesni ekvator in ekliptika se sekata v pomladišču $\gamma$ . V tej točki je Sonce ob pomladanskem enakonočju, ki nastopi 19., 20. ali 21. marca. V tej točki velja $\delta_{\odot}=0\degr$ in $\alpha_{\odot}=0^{\rm h}$ . Dan je povsod dolg 12 ur, Sonce vzide točno na vzhodu in zaide točno na zahodu.
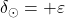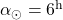Od pomladanskega enakonočja do poletnega solsticija se Soncu povečujeta rektascenzija in deklinacija. Ob poletnem solsticiju, ki nastopi med 20. in 22. junijem, je $\delta_{\odot}=+\varepsilon$ in $\alpha_{\odot}=6^{\rm h}$ . Na severni polobli Sonce vzhaja na severovzhodu in zahaja na severozahodu.
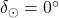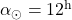Po poletnem solsticiju deklinacija Sonca (in s tem opoldanska višina na nebu nad opazovališčem na severni polobli) pada. Ob jesenskem enakonočju, ki nastopi med 22. in 24. septembrom, je $\delta_{\odot}=0\degr$ in $\alpha_{\odot}=12^{\rm h}$ . Sonce je v drugem presečišču ekliptike in nebesnega ekvatorja. Vzide točno na vzhodu in zaide točno na zahodu.
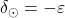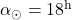Ob zimskem solsticiju (ki nastopi med 20. in 23. decembrom) ima Sonce $\delta_{\odot}=-\varepsilon$ in $\alpha_{\odot}=18^{\rm h}$ . Na severni polobli Sonce vzide na jugovzhodu in zaide na jugozahodu. Opoldanska višina Sonca je najnižja v letu.
Po zimskem solsticiju prične deklinacija spet naraščati in doseže vrednost 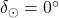$\delta_{\odot}=0\degr$ v pomladišču. Rektascenzija je 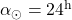$\alpha_{\odot}=24^{\rm h}$ oziroma 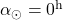$\alpha_{\odot}=0^{\rm h}$ . Leto je naokoli.

Kako visoko je Sonce na nebu?

Izračunajte, kako visoko na nebu je Sonce v najvišji točki, če ga opazujemo iz Ljubljane ( $\phi = 46\degr$ ) ob:

pomladanskem enakonočju
poletnem solsticiju
jesenskem enakonočju
zimskem solsticiju

Odgovori

$44\degr$ , $67.5\degr$ , $44\degr$ in $20.5\degr$

Kdaj je dan zares enako dolg kot noč?

Ob enakonočju svetli del dneva v resnici ne traja natanko 12 ur. Zaradi sipanja Sončeve svetlobe v Zemljinem ozračju je namreč svetlo že pred vzhodom Sonca (zora), stemni pa se šele po njegovem zahodu (mrak). Tudi če bi svetli del dneva definirali kot čas, ko je Sonce nad obzorjem, ne velja povsem točno, da je ob enakonočju to 12 ur. Pri računanju časa enakonočja namreč privzamemo, da je Sonce točka, medtem ko je v resnici disk. Ob enakonočju je tako dan daljši od noči. Dan in noč sta enako dolga nekaj dni pred pomladnim in nekaj dni po jesenskem enakonočju.

Medtem ko je lahko določiti ekvatorski koordinati Sonca v štirih posebnih točkah (ob enakonočjih in solsticijih), je opisati gibanje Sonca med zvezdami na nebu ob drugih dnevih leta trši oreh. Iz dveh razlogov: ker je ekliptika nagnjena glede na nebesni ekvator in ker je Zemljina tirnica elipsa.

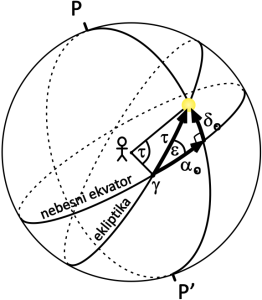
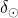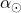Slika 3.2: Sončevi koordinati $\delta_{\odot}$ in $\alpha_{\odot}$ se skozi leto ne spreminjata enakomerno.

Najprej predpostavimo, da se Zemlja okoli Sonca giblje po krožnici. V tem primeru bi bila njena kotna hitrost konstantna, torej bi se tudi Sonce gibalo s konstantno kotno hitrostjo po ekliptiki. Označimo kot, ki ga Sonce opravi na ekliptiki s $\tau$ (slika 3.2). Iz predpostavke enakomernega kroženja sledi, da Sonce vsak dan opravi pot $360\degr/365,25 = 59\arcmin 8\arcsec$ . A kot je razvidno s slike, koordinati $\delta_{\odot}$ in $\alpha_{\odot}$ zaradi nagnjenosti ekliptike glede na nebesni ekvator ne naraščata sorazmerno s časom.

Gibanje Sonca

S pomočjo in uporabe kosinusnega in sinusnega izreka pokažite, da se Sončevi koordinati v primeru, da je Zemljina orbita krožnica, spreminjata kot:

(1) $\begin{eqnarray*} \tan \alpha_\odot &=& \cos \epsilon \tan \tau \\ \sin \delta_\odot &=& \sin \epsilon \sin \tau \end{eqnarray*}$

A Zemljina tirnica okoli Sonca ni krožnica, temveč elipsa. Njena kotna hitrost okoli Sonca, in s tem navidezna hitrost Sonca po ekliptiki, se spreminja. Hitrost je največja okrog 3. janurja, ko je Zemlja najbliže Soncu (tej točki rečemo perihelij ali prisončje), in najmanjša okrog 4. julija, ko je najdlje od njega (tej točki rečemo ahelij ali odsončje). Posledično je opis koordinat Sonca skozi leto zapleten.

Koordinate Sonca na določen dan lahko najdemo v efemeridah in programih, kot je Stellarium, ter na številnih spletnih straneh.

Letni časi

Letni časi so neposredna posledica nagnjenosti ekliptike glede na nebesni ekvator oziroma Zemeljine osi vrtenja glede na pravokotnico na ekliptiko, in niso, kot bi morda pomislili, posledica sploščenosti Zemljine tirnice. Pravzaprav je Zemlja Soncu najbliže 3. januarja, ko je na severni polobli zima. Sploščenost Zemljine tirnice na letne čase nima (velikega) vpliva.

Slika 3.3: Pot Sonca po nebu se med letom spreminja.

Pot Sonca po nebu je shematično narisana na sliki 3.3, tokrat v horizontnem sistemu. Primerjajmo pot Sonca po nebu ob poletnem in zimskem solsticiju. Poleti je v opazovališču na severni polobli Sonce več časa nad obzorjem in više na nebu. Sonce torej dalj časa segreva severno poloblo. Poleg tega jo bolj greje, saj višina na nebu vpliva na kot, pod katerim Sončevi žarki padajo na Zemljo — večja višina pomeni, da žarki padajo pod večjim kotom, s tem pa je prejeta količina svetlobe na enoto površine večja. Za južno poloblo velja ravno obratno.

Slika pokaže še, da se točka vzhoda in zahoda Sonca skozi leto spreminja. Na primer, poleti Sonce vzhaja proti severovzhodu, zahaja pa proti severozahodu.

Interaktivno

Spreminjanje dolžine dneva na različnih zempljepisnih širinah je prikazano tukaj. Spreminjanje letnih časov in vpadnega kota Sončevih žarkov prikazuje ta simulacija.

Pravi in srednji Sončev čas

V prejšnjem poglavju smo definirali krajevni zvezdni čas kot časovni kot pomladišča (enačba 2). Na osnovi dnevnega gibanja pomladišča lahko definiramo še zvezdni dan kot čas med dvema zaporednima zgornjima kulminacijama pomladišča.

V vsakdanjem življenju za določanje časa seveda ne uporabljamo točke $\gamma$ . Čas, ki ga merijo naše ure, je povezan z dnevnim gibanjem Sonca, ki uravnava naš biološki ritem. Pravi Sončev čas $t_{\lambda}^{\odot}$ je definiran kot časovni kot pravega Sonca $H_{\odot}$ . Čas, ki mine med dvema zaporednima kulminacijama pravega Sonca, je en pravi Sončev dan. Zakaj govorimo o pravem Soncu? Morda ste že posumili, da se dolžina tako definiranega dneva skozi leto spreminja (enačba 2), ker rektascenzija Sonca ne narašča enakomerno s časom.

Seveda ne bi bilo praktično, če bi se dolžina dni v letu med seboj razlikovala. Zato za potrebe merjenja časa definiramo srednje Sonce. To je namišljeno telo, ki se giblje po nebesnem ekvatorju (ne po ekliptiki, kot pravo Sonce), naredi en obhod v enem letu in ima vedno $\delta_{\rm S} = 0\degr$ . Pravo in srednje Sonce imata v pomladišču enaki koordinati, od tod naprej rektascenzija srednjega Sonca narašča linearno s časom:

(2) $\begin{equation*} \alpha_{\rm S} = kt \end{equation*}$

Pri tem je $k = 360\degree/365,25$ dni = $59\arcmin 8\arcsec$ na dan. Čas srednjega Sonca definiramo, podobno kot pri pravem Soncu, kot časovni kot srednjega Sonca:

(3) $\begin{equation*} t_{\lambda}^{\rm S} = H_{\rm S} \end{equation*}$

Srednji Sončev dan je enak času, ki mine med dvema zaporednima kulminacijama srednjega Sonca. Dolžina srednjih Sončevih dni je skozi leto vedno enaka.

Razliko med pravim in srednjim Sončevim časom podaja časovna enačba. Slika 3.4 prikazuje to razliko skozi leto. Prve tri mesece pravi Sončev čas zaostaja za srednjim, kar praktično pomeni, da Sonce pride na poldnevnik nekaj minut po tem, ko naša ura pokaže poldne. V zadnjem delu leta pravi Sončev čas prehiteva.

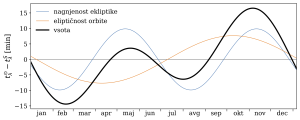
Slika 3.4: Razlika med pravim in srednjim Sončevim časom je vsota dveh prispevkov: prispevka zaradi eliptičnosti Zemljine orbite (s periodo 1 leta) in prispevka zaradi nagnjenosti ekliptike glede na nebesni ekvator (s periodo pol leta).

Za merjenje časa uporabljamo srednji Sončev čas, ki je po definiciji enak časovnemu kotu srednjega Sonca (enačba 3). Za vsakdanjo rabo so vpeljali meščanski čas:

(4) $\begin{equation*} t_{\lambda}^{\rm m} = t_{\lambda}^{\rm S} + 12^{\rm h}, \end{equation*}$

ki je premaknjen za 12 h. S tem so zagotovili, da se nov dan ne začne, ko je Sonce v kulminaciji (okoli poldneva), temveč sredi noči. V nekateri literaturi definicija srednjega Sončevega časa že vsebuje prištetih 12 h.

Analema

Če vsak dan v letu ob isti uri slikamo isti del neba in združimo slike, vidimo, da Sonce na nebu opiše lik, poodben osmici. Tej figuri pravimo analema. Sprememba položaja v navpični smeri je posledica spremembe deklinacije Sonca zaradi nagnjene osi Zemlje. Sprememba položaja v vodoravni smeri je posledica neenakomerno spreminjajoče se rektascenzije, torej kombinacije nagnjene osi vrtenja in sploščenosti Zemljine tirnice. Oblika analeme je odvisna od geografske širine in ure v dnevu, ko snemamo Sonce. Kakšno analemo bi videla opazovalka ali opazovalec na ekvatorju?

Interaktivno

Za lažjo predstavo časovne enačbe si poglejte animacijo.

Časovni pasovi

Vsi časi, ki smo jih omenili doslej — pravi in srednji Sončev ter meščanski čas — so krajevni, merjeni od krajevnega nebesnega poldnevnika, in zato odvisni od opazovališča, točneje od njegove zemljepisne dolžine $\lambda$ . Zato smo jim dodali indeks $\lambda$ . Da bi se izognili zmedi pri merjenju časa na okrogli Zemlji, so definirali referenčno točko, glede na katero merimo čas. Kot pri koordinatah je to greenwiški nebesni poldnevnik.

Slika 3.6: Časovni kot na krajih z različno geografsko dolžino.

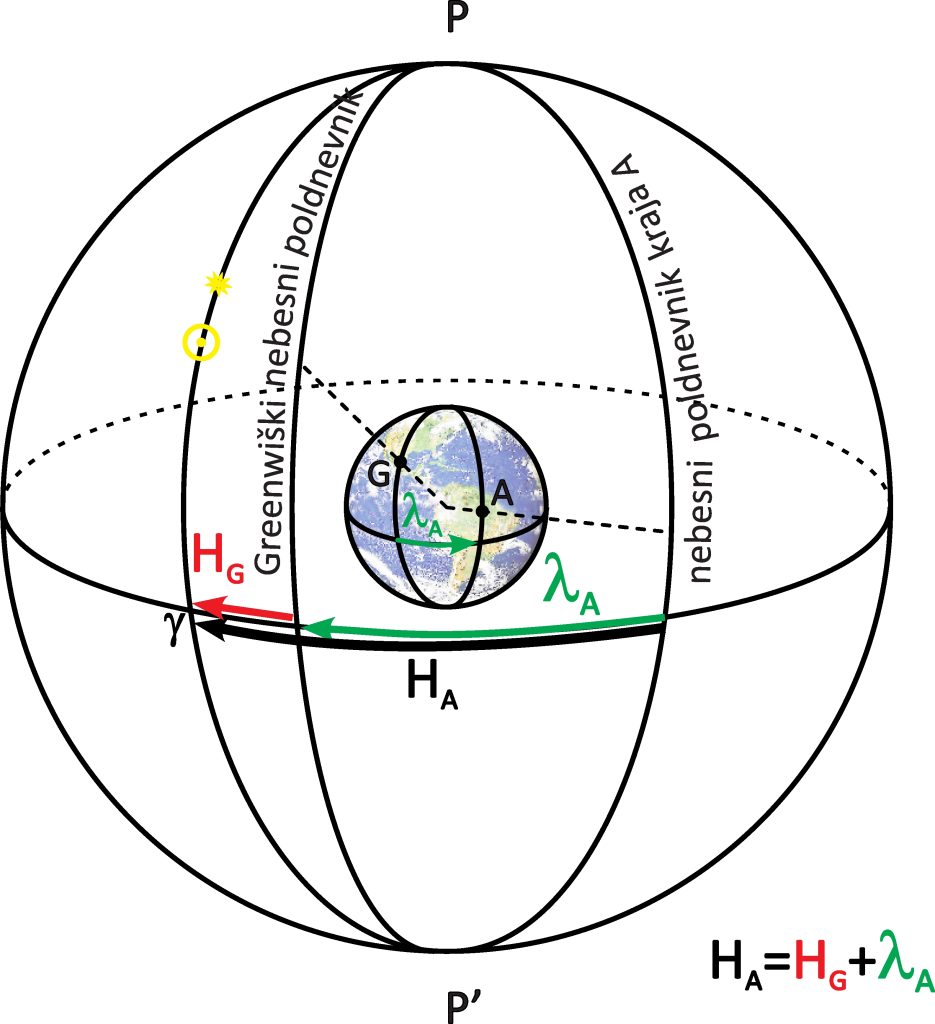
Na sliki 3.6 sta dve opazovališči, eno v kraju A z geografsko dolžino $\lambda_{\rm A}$ in drugo v Greenwichu z geografsko dolžino $\lambda_{\rm G}$ . Časovni kot nekega telesa, pa naj bo to Sonce, zvezda ali pomladišče, merjen iz opazovališča A, je $H_{\rm A}$ , časovni kot, merjen iz Greenwicha pa $H_{\rm G}$ . S slike razberemo, da velja:

(5) $\begin{equation*} H_{\rm A} = H_{\rm G} + \lambda_{\rm A} \end{equation*}$

Spomnimo se, da je krajevni čas (bodisi zvezdni, pravi Sončev čas, srednji Sončev čas ali meščanski čas) pravzaprav časovni kot (točke gama pravega Sonca, srednjega Sonca oziroma srednjega Sonca + 12 h) (enačba 3), torej lahko zgornjo enačbo prepišemo kot:

(6) $\begin{equation*} t_{\rm A} = t_{\rm G} + \lambda_{\rm A}, \end{equation*}$

kjer geografsko dolžino izrazimo v urah ( $1^{\rm h}$ ustreza $15\degr$ ).

Krajevni meščanski čas na greenwiškem poldnevniku je po dogovoru določen kot svetovni čas oziroma angleško Universal Time (UT):

(7) $\begin{equation*} UT = t_{\rm \lambda=0}^{\rm m} \end{equation*}$

Meščanski čas na drugi geografski dolžini je po enačbi 6 potem:

(8) $\begin{equation*} t_{\lambda}^{m} = UT + \lambda \end{equation*}$

Kraji na različnih poldnevnikih imajo torej različen krajevni čas. (Vsi kraji na istem poldnevniku imajo isti krajevni čas.) Če se geografska dolžina dveh krajev razlikuje za $1\degr$ , se krajevni čas med krajema razlikuje za 4 minute.

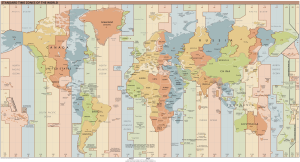
V vsakdanjem življenju bi bilo zelo nepraktično, če bi uporabljali krajevni meščanski čas, zato so v drugi polovici 19. stoletja uvedli conski čas. Nastale so cone oziroma časovni pasovi, široki $15\degr$ (slika 3.7). Čas v dveh sosednjih conah se razlikuje za $1^{\rm h}$ . Cone, zaradi praktičnosti, večinoma sledijo državnim mejam, zato meje med časovnimi pasovi niso povsod ravne.

Slika 3.7: Časovni pasovi. Avtorji: UnaitxuGV, Heitordp and others (public domain)

Posamezen časovni pas označimo s številom $n$ : za greenwiški pas je $n=0$ , pasovi vzhodno od Greenwicha imajo $n=1^{\rm h},\cdots,12^{\rm h}$ , časovni pasovi zahodno od Greenwicha $n=-1^{\rm h},\cdots,-12^{\rm h}$ . Z enačbo zapišemo conski čas kot:

(9) $\begin{equation*} t_{\rm n}^{\rm z} = UT + n \end{equation*}$

V nekaterih državah, tudi v Sloveniji, v poletnem času uvajamo tako imenovani poletni čas. V Sloveniji (Evropi) zadnji konec tedna v marcu v noči s sobote na nedeljo premaknemo ure za 1 h naprej in zadnji konec tedna oktobra za 1 h nazaj. Med poletnim časom moramo zato conskemu času prišteti še 1 h, da dobimo čas, ki nam ga kaže ura. Opomnimo, da do premika ure v vseh državah ne pride istočasno, zato je pri načrtovanju mednarodnih sestankov ali astronomskega opazovanja na daljavo potrebna še posebna previdnost.

Zvezdni in Sončev čas

Zvezdni in Sončev čas se razlikujeta, kar je posledica gibanja Zemlje okoli Sonca.

Predstavljajmo si, da z Zemlje opazujemo položaj Sonca in neke zvezde. Za lažjo predstavo naj bosta v nekem trenutku zvezda in Sonce na krajevnem nebesnem poldnevniku. V tem trenutku je v tem kraju poldne. Potem ko se Zemlja enkrat zavrti okoli svoje osi, bo zvezda, ki je veliko dlje od Zemlje kot Sonce, zopet na nebesnem poldnevniku — minil je en zvezdni dan.

Kaj pa Sonce? Po enem Zemljinem vrtljaju Sonce še ne bo na nebesnem poldnevniku, zato se bo morala Zemlja še nekoliko zavrteti, da bo Sonce spet na nebesnem poldnevniku (in bo spet poldne), kar je prikazano na sliki 3.8.

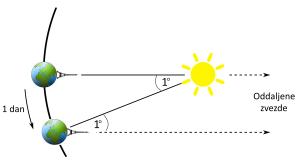
Slika 3.8: Slika prikazuje, zakaj nastane razlika med zvezdnim in Sončevim dnevom.

Dodatno vrtenje je potrebno, ker se Zemlja med enim vrtljajem na svoji tirnici premakne okoli Sonca. Za isti kot, kot se premakne Zemlja, se mora dodatno zavrteti, da bo spet poldne. Ta kot je v povprečju $58\arcmin 59\arcsec$ , kar ustreza času $3^{\rm m}56^{\rm s}$ . Sončev dan, ki traja $24^{\rm h}$ , je torej slabe štiri minute daljši od zvezdnega dne. Za toliko se poveča razlika med Sončevim časom in zvezdnim časom vsak dan in se kopiči iz dneva v dan ter v enem letu zraste na cel dan. Kar je razumljivo, saj v enem letu Zemlja naredi 365,242 obrata glede na Sonce (eno leto traja 365,242 srednjega Sončevega dne) ter enega dodatnega glede na zvezde (ker naredi en obhod okoli Sonca).

Zvezdni in Sončev čas se ujemata ob pomladnem enakonočju. Nato tečeta z malenkost različno hitrostjo, dokler se v naslednjem pomladnem enakonočju spet ne ujameta.

Kolikokrat se obrne kovanec?

Koliko obratov naredi kovanec, ki ga zavrtimo okoli drugega, enako velikega kovanca?

Odgovor

2

Slika 3.9: Koliko obratov naredi kovanec?

Če se vam odgovor zdi presenetljiv, še enkrat preberite zadnje poglavje.

Julijanski dan in datum

V tem gradivu se ne bomo posebej posvečali koledarjem. Omenimo le sistem, ki ga uporabljajo astronomi (in ga boste običajno našli v katalogih), s katerim enostavno izračunamo čas, ki je pretekel med dvema dogodkoma.

Astronomi za merjenje časa uporabljajo julijanski dan. Šteti začnemo 1. januarja 4713 pr. n. št. opoldne po julijanskem koledarju^[2]. Julijanske dneve od dneva 0 enostavno štejemo kot cela števila.

Na primer, da hočemo zapisati čas opazovanja. Najprej preštejemo, koliko dni je preteklo od začetka štetja. Če smo opazovali 7. februarja 2025, je to število enako 2460713. Natančen čas opazovanja tega dne zapišemo tako, da celemu številu dodamo decimalni del. Če smo opazovali ob 12.00, bo to 0,5 (smo na polovici dneva) in čas opazovanja postane 2460713,5. V tabelah boste to številko našli pod oznako JD (Julian Date).

Ker je julijanski dan tako veliko število, se v praksi uporabljajo različni sistemi, ki za začetno točko vzamejo neki drug datum. Astronomi radi uporabljajo MJD (Modified Julian Date):

(10) $\begin{equation*} MJD = JD - 2400000.5 \end{equation*}$

Gibanje planetov

Ne le Zemlja, tudi mnoga druga telesa v Osončju se gibljejo okoli Sonca: planeti, asteroidi, meteoroidi, kometi. Zaradi lastnega gibanja^[3] okoli Sonca lahko projekcije smeri planetov na nebesno sfero opisujejo kar zapletene poti.

Zanimiv pojav je navidezno retrogradno gibanje planetov. Kot opazovalci in opazovalke smo na planetu, ki se tako kot drugi planeti giblje okoli Sonca. Hitrost gibanja planeta je odvisna od oddaljenosti od Sonca, zato se relativna hitrost in relativni položaj glede na Sonce nenehno spreminjata (slika 3.10). Recimo, da opazujemo Mars. Ker Zemlja okoli Sonca potuje hitreje kot Mars, bo na neki točki Mars začel zaostajati in posledično se bo navidezno (glede na opazovalca na Zemlji) gibal vzvratno (retrogradno).

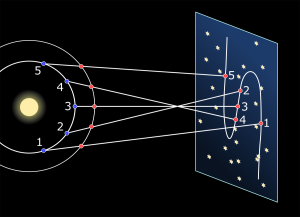
Slika 3.10: Prikaz retrogradnega gibanja. Na liki vidimo položaj Marsa (rdeča) glede na oddaljene zvezde, kakor ga vidimo z Zemlje (modra). Avtor: Brian Brondel (CC BY-SA 3.0)

Retrogradno gibanje lahko opazimo pri vseh telesih, ki so od Zemlje bolj oddaljena od Sonca (planeti, asteroidi, meteoroidi, kometi). Do retrogradnega gibanja pride tudi pri Veneri in Merkurju, a ga je teže opaziti, saj nam je v napoto svetlo Sonce.

Opazovalci na Merkurju

Tudi z drugih teles Osončja bi videli navidezno retrogradno gibanje. Morda najbolj nenavadne stvari bi se dogajale na Merkurju, kjer včasih celo Sonce potuje retrogradno. Ko je Merkur najbliže Soncu, je njegova orbitalna hitrosta večja od hitrosti vrtenja. Sonce takrat vzide, nato zaide, in nato ponovno vzide.

Navideznega retrogradnega gibanja ne smemo mešati s pravim retrogradnim gibanjem. Poznamo nekaj deset asteroidov, ki se okoli Sonca gibljejo v drugi smeri kot preostala telesa Osončja. Pravimo, da so na retrogradni orbiti.

Tudi nekatere lune zunanjih planetov se gibljejo v drugi smeri, kot se gibljejo planeti okoli Sonca in večina lun okoli planetov, to je — gledano iznad Zemljinega severnega pola — v nasprotni smeri urnih kazalcev. Na primer, Neptunova luna Triton se giblje v smeri urnih kazalcev — ima retrogradno orbito.

V literaturi se izraz ekliptika uporablja tudi namesto ekliptične ravnine, zato je vedno dobro paziti na kontekst, v katerem se termin uporablja. ↵
Po gregorijanskem koledarju ta datum ustreza 24. novembru 4714 pr. n. št. ↵
Lastnega gibanja zvezd tukaj ne bomo posebej obravnavali. ↵

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Uvod v astronomska opazovanja za dijake in dijakinje Copyright © 2025 by University of Nova Gorica Press is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.