Fotometrija

Jure Japelj; Andreja Gomboc

10 Fotometrija

Jure Japelj and Andreja Gomboc

Fotometrija je tehnika merjenja svetlobnega toka oziroma navideznega sija astronomskih teles. S fotometrijo kvantitativno izmerimo navidezni sij zvezd, da jih lahko nato med seboj primerjamo. Ob znani oddaljenosti zvezde ji s tem izmerimo tudi izsev (L) in absolutni sij. Absolutni in navidezni sij podajamo v magnitudah (mag).

Oblike zvezd na slikah

Zvezde so tako daleč, da ne moremo razločiti njihove površine in jih tako ne moremo opazovati kot telesa. Na nebu so videti kot točkasta svetila, a na posnetku iz razlogov, predstavljenih v 6. poglavju, zavzemajo določeno površino tudi takrat, ko je slika ostra. Velikost površine je teoretično omejena z velikostjo vstopne odprtine teleskopa oziroma kotno ločljivostjo (poglavje Teleskopi), v praksi pa običajno z migljanjem ozračja oziroma seeingom. Oblika in velikost zvezde na posnetku sta odvisni od teleskopa, instrumentov in kamere, s katerimi opazujemo.

Svetle zvezde so na posnetkih zelo opazne. Iz njih izhajajo ostre, svetle konice. Nastanejo pri uklanjanju svetlobe na opornikih, ki držijo sekundarno zrcalo (spomnimo se, da imajo zrcalni teleskopi običajno primarno in sekundarno zrcalo). Število in postavitev opornikov vplivata na obliko in razporeditev konic (slika 10.1). Iz uklonskega vzorca na sliki lahko ugotovimo, kakšna je postavitev opornikov in obratno — iz znane postavitve opornikov lahko napovemo, kakšen bo uklonski vzorec. Velja poudariti, da je ta vzorec enak za vse zvezde, a je opazen le pri visokem signalu, zato ga vidimo le pri najsvetlejših zvezdah na sliki.

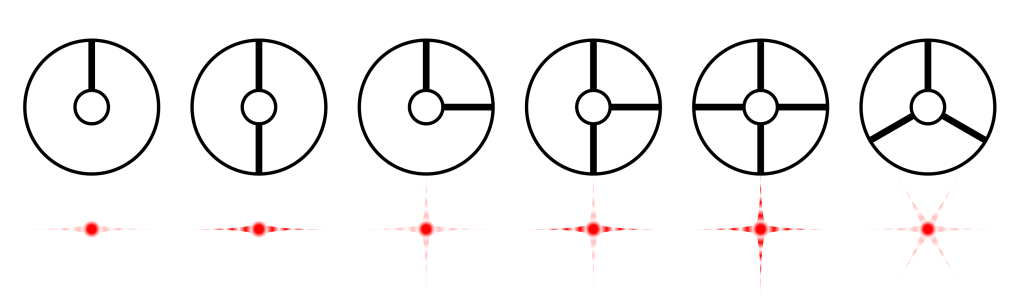
Slika 10.1: Uklonski vzorec zvezd pri različni postavitvi opornikov sekundarnega zrcala glede na vhodno odprtino teleskopa. Avtor: Cmglee (CC BY-SA 3.0)

Poleg opornikov na uklonski vzorec vpliva tudi oblika primarnega zrcala, kar lepo ponazarja primerjava vzorcev zvezd, posnetih z vesoljskima teleskopoma Hubble in James Webb (slika 10.2). Prvi ima okroglo primarno zrcalo, sekundarno zrcalo držijo štirje oporniki. Drugi ima primarno zrcalo v obliki šestkotnika, sekundarno zrcalo držijo trije oporniki. Pri Vesoljskem teleskopu James Webb vzorec dodatno zasoli sestavljeno zrcalo (primarno zrcalo je sestavljeno iz 18 manjših zrcal).

Slika 10.2: Primerjava uklonskega vzorca vesoljskih teleskopov Hubble in James Webb. Foto: NASA’s James Webb Space Telescope (CC BY 2.0)

Kot rečeno, imajo vse zvezde enak uklonski vzorec. Natančno merjenje signala mora zato upoštevati zapletene vzorce. A če se osredotočimo na zvezde, ki niso tako svetle, da bi imele znatne uklonske konice, teh težav ni. Zvezda, ki ji želimo izmeriti sij, mora biti torej posneta s takim časom osvetlitve, da z nje ne prejmemo preveč signala. Obenem pa signala ne sme biti premalo, saj bi to vodilo do velike negotovosti meritve sija.

Uklonski vzorci na spletu

Na spletu poiščite slike svetlih zvezd ali galaksij in identificirajte različne uklonske vzorce.

Signal, šum in negotovost

Pri vsaki meritvi je nekaj negotovosti, saj ničesar ne moremo izmeriti z absolutno natančnostjo. Tako je tudi z navideznim sijem zvezd. Poglejmo si nekaj splošno uporabljenih terminov.

Signal je število fotoelektronov, ki jih zberemo na kameri in pretvorimo v elektronsko obliko.

Šum je motnja, ki se je prikradla v signal in se odraža v negotovosti njegove izmerjene vrednosti. Štirje glavni prispevki šuma so:

Šum zaradi naključnega prihajanja fotonov zvezde. Tako rekoč vsi sevalci v vesolju sevajo fotone naključno. Recimo, da zvezdo opazujemo trikrat po eno sekundo. Signal zvezde, ki ga izmerimo, je enkrat 10, drugič 12, tretjič pa 9 fotoelektronov. Z drugimi besedami: če zvezda v povprečju oddaja 10 fotonov na sekundo, to ne pomeni, da bomo mi v vsaki sekundi prejeli 10 fotonov. Takšnemu šumu pravimo tudi Poissonov šum. Negotovost v primeru Poissonovega šuma 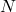$N$ je enaka 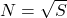$N = \sqrt{S}$ , kjer je 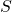$S$ število fotonov, ki jih v določenem času prejmemo od zvezde.
Šum zaradi naključnega prihajanja fotonov ozadja. Tudi nebo seva v vidni svetlobi. Na območju slike, kjer ni zvezd, zato izmerimo neki od nič različen signal. Ta signal ozadja prispeva tudi k signalu zvezd. Pridelamo šum neba oziroma šum ozadja. Tako kot zvezda tudi nebo fotone seva naključno.
Šum temnega toka na senzorju svetlobe v kameri (glej poglavje Kamere).
Bralni šum pri pretvorbi zbranega naboja na pikslih kamere v električni signal (napetost). Pri tem elektronika (ojačevalnik) na senzorju dodatno poveča delež šuma pri izmerjeni vrednosti. Bralni šum je enak za vse piksle na senzorju in je odvisen od vrste senzorja.

Pogosto uporabljen termin je razmerje signal proti šumu ( $S/N$ ). Kot pove že samo ime, gre za primerjavo signala in šuma; višji ko je $S/N$ , več imamo signala v primerjavi s šumom, boljša je naša meritev. Signal proti šumu lahko vzamemo za oceno kvalitete izmerjenih podatkov. Če iz podatkov ne moremo izluščiti pravega signala, ki je posledica opazovanja želenega nebesnega telesa, rezultatom na podlagi takšnih meritev ne moremo zaupati. Za lažjo predstavo so na sliki 10.3 prikazani posnetki zvezd z različnimi vrednostmi $S/N$ . Pri $S/N = 2$ je slika zvezde tako neizrazita, da ne moremo z visoko gotovostjo trditi, da je zvezda res tam. Pri $S/N = 5$ je zvezda dobro vidna in običajno lahko pri tej vrednosti $S/N$ trdimo, da gre za detekcijo. Pri $S/N = 10$ fotometričnim meritvam lahko začnemo zaupati. Z naraščanjem $S/N$ postajajo meritve sija vedno bolj natančne. Negotovost meritve pri $S/N = 100$ je že izredno majhna.

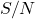SLika 10.3: Primeri zvezd z različnimi vrednostmi razmerja med signalom in šumom $S/N$ . Posneto s teleskopom GoChile-GoT1.

Zavedati se moramo, da ne moremo vedno imeti visokega signala proti šumu. Včasih smo zadovoljni že s tem, da neko oddaljeno, temno galaksijo sploh detektiramo. V drugih primerih, kot je opazovanje zapletenega utripanja zvezdnih atmosfer, pa potrebujemo izjemno natančne meritve in torej zelo visok $S/N$ . Zadostna vrednost $S/N$ je tako odvisna od okoliščin.

Merjenje signala in instrumentalni sij

Signal zvezde najenostavneje izmerimo tako, da seštejemo ves signal s pikslov znotraj nekega radija okoli zvezde. Pravimo, da signal izmerimo znotraj aperture.

Slika 10.4: Običajna apertura za merjenje signala zvezde.

Običajna apertura je shematično prikazana na sliki 10.4. Ideja je preprosta:

seštejemo ves signal znotraj notranjega kroga ( $S_{\rm vse}$ );
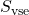zunanji kolobar ne vsebuje nobene zvezde, zato signal v kolobarju uporabimo za izračun povprečnega signala neba oziroma ozadja na pikslu ( $S_{\rm ozadje}$ );
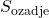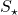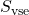
končni rezultat, torej signal zvezde, je 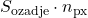$S_{\star}$ = $S_{\rm vse}$ $-$ $S_{\rm ozadje}\cdot n_{\rm px}$ , pri čemer je 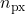$n_{\rm px}$ število pikslov znotraj notranjega kroga (število pikslov, na katere pade slika zvezde).

Sedaj lahko izračunamo instrumentalno magnitudo oziroma instrumentalni sij:

(1) $\begin{equation*} m_{\rm ins} = -2.5\log_{10}\left( \frac{S_{\star}}{t_{\rm osv}}\right) \end{equation*}$

Pri tem je $t_{\rm osv}$ čas osvetlitve. Instrumentalni sij je odvisen od teleskopa, instrumenta in vremenskih razmer. Na primer, z večjim teleskopom ujamemo več fotonov zvezde kot z manjšim, zato bo instrumentalni sij, izmerjen z večjim premerom objektiva (in ob predpostavki, da so vremenske razmere enake), manjši (kar pomeni več signala).

Nedoločenost instrumentalnega sija

Kolikšna je absolutna nedoločenost instrumentalnega sija $\Delta m_{\rm ins}$ , če poznate nedoločenost izmerjenega signala $\Delta S_{\star}$ ?

Ker je enačba 1 nelinearna, to ni preprosto izračunati. Izkaže se, da morate uporabiti enačbo:

(2) $\begin{equation*} \Delta m_{\rm ins} = \frac{2.5}{S_{\star}\ln{10}}\Delta S_{\star}. \end{equation*}$

Instrumentalni sij moramo umeriti, da dobimo navidezni sij, ki bo dejansko povedal, kako svetla je zvezda. Navidezni sij lahko nato primerjamo tudi z vrednostmi sija, ki so jih izmerili drugi opazovalci. Zapišimo navidezni sij:

(3) $\begin{equation*} m = m_{\rm ins} + ZP = -2.5\log_{10}\left( \frac{S_{\star}}{t_{\rm osv}}\right) + ZP \end{equation*}$

Pri tem je $ZP$ ničelni sij (ang. zero point). Tako kot instrumentalni je tudi ničelni sij odvisen od teleskopa, instrumenta in vremenskih razmer. Preden si pogledamo, kako dobimo vrednost $ZP$ , moramo uvesti še nekaj konceptov.

Filtri

V poglavju o barvah smo že omenili, da nebesna telesa pogosto opazujemo skozi filtre, steklene ploščice, ki prepustijo le omejen pas valovne dolžine.

Širokopasovni filtri prepustijo okoli 100 nm široke pasove, ozkopasovni filtri desetkrat manj. S širokopasovnimi filtri opazujemo zvezde, galaksije in na splošno tista telesa, ki imajo bolj ali manj zvezen spekter. Z ozkopasovnimi filtri opazujemo meglice in nekatere galaksije, ki sevajo emisijske črte.

Komplet filtrov, s katerim pokrijemo široko območje valovnih dolžin, imenujemo fotometrični sistem. Omenimo dva izmed najbolj znanih fotometričnih sistemov. Prvi je tradicionalen $UBVRI$ ali sistem Johnson-Morgan-Cousins. Primer novejšega sistema je $u'g'r'i'z'$ , ki so ga prvič uporabili za opazovanje v okviru velikega pregleda neba SDSS (Sloan Digital Sky Survey). Črke filtrov nakazujejo, kateri del spektra svetlobe prepustijo. Filter $B$ prepusti modro svetlobo, filter $R$ rdečo, filter $G$ zeleno in tako dalje^[1].

Črke uporabljamo tudi pri zapisu sija, izmerjenega skozi posamezen filter. Na primer, navidezni sij, izmerjen skozi filter $R$ , zapišemo kot $m_{\rm R} = 15$ mag ali še preprosteje $R = 15$ mag.

Standardna zvezda Vega

Sij vedno podamo glede na neko referenčno vrednost (glej poglavje Nočno nebo in enačbo 2). Da bi zapis nekoliko poenostavili, so se v preteklosti dogovorili, da ima zvezda Vega sij enak 0 mag (izmerjeno v vseh filtrih). Pravimo, da je Vega standardna fotometrična zvezda. Ko rečemo, da ima neka zvezda sij $m_{\rm R} = 5$ mag, je to ekvivalentno izjavi:

(4) $\begin{equation*} m_{\rm R} = m_{\rm R, Vega} - 2,5\log_{10}{{j_{\rm R}}\over {j_{\rm R, Vega}}} = - 2,5\log_{10}{{j_{\rm R}}\over {j_{\rm R, Vega}}} = 5~{\rm mag} \end{equation*}$

Pri tem smo upoštevali $m_{\rm R, Vega} \equiv 0$ . Če poznamo sij neke zvezde, lahko po tej enačbi izračunamo, kolikšno gostoto svetlobnega toka bi izmerili za zvezdo v primerjavi z Vego.

Če je sij umerjen glede na Vego, govorimo o Veginem sistemu magnitud. Opozorimo, da lahko sij umerimo tudi drugače. Pogosto uporabljen sistem magnitud je tudi sistem AB. V tem primeru je standardna zvezda umetno definirana zvezda, ki ima v celotnem spektru enako spektralno gostoto toka^[2]. V katalogih boste praviloma našli podatek, v katerem sistemu so umerjeni podani siji.

Diferencialna fotometrija

Instrumentalni sij opazovanega telesa najlaže umerimo glede na druge zvezde na istem posnetku. Postopek je sledeč.

Slika 10.5: Primer merjenja navideznega sija v programu AstroImageJ. Z zeleno aperturo merimo signal našega telesa, z rdečimi aperturami pa signal primerjalnih zvezd, katerih pravi sij preberemo v katalogu.

Izberemo optimalno velikost aperture, s katero bomo merili signal želenega telesa (na zgornji sliki je to zelena apertura). Nato izberemo več zvezd na sliki s primerljivim signalom in znanim sijem^[3] in tudi njim izmerimo signal z aperturo enake velikosti (rdeče aperture na sliki). Signal, ki ga izmerimo skozi posamezno aperturo, pretvorimo v instrumentalni sij po enačbi 1. Za vsako primerjalno zvezdo izračunamo ničelni sij po enačbi 3. Nato izračunamo povprečen ničelni sij in ga prištejemo instrumentalnemu siju našega telesa, da dobimo njegov navidezni sij.

Pri izbiri primerjalnih zvezd je potrebna previdnost, da med njimi ni kake spremenljive zvezde. Če se izmerjeni ničelni sij za katero izmed primerjalnih zvezd znatno razlikuje od drugih, je to vrednost najbolje zavreči in si izbrati drugo primerjalno zvezdo. Več primerjalnih zvezd ko boste izbrali, natančnejša bo umeritev. Pri računanju povprečja (ali mediane) ne pozabite izračunati negotovosti povprečja. To negotovost morate prišteti negotovosti instrumentalnega sija (enačba 2).

Fotometrija s standardno zvezdo

Včasih se zgodi, da na sliki ni zvezde (oziroma dovolj velikega števila zvezd) z znanim sijem, kar prepreči uporabo diferencialne fotometrije. V tem primeru je postopek umeritve instrumentalnega sija bolj zapleten. Tukaj ne bomo šli v podrobnosti, temveč bomo le omenili glavno idejo.

Med opazovanjem moramo poleg našega telesa opazovati še standardno zvezdo na drugem delu neba (z istimi filtri in nastavitvami kamere), katere sij poznamo. Izmerimo instrumentalni sij standardne zvezde in s primerjanjem instrumentalnega in navideznega sija izmerimo ničelni sij $ZP$ . Če bi opazovali iz vesolja, bi ničelni sij enostavno prišteli instrumentalnemu siju našega telesa in stvar bi bila končana.

Če opazujemo z Zemlje, je med nami in telesom ozračje. Ozračje absorbira in siplje del svetlobe, čemur pravimo ekstinkcija ozračja. Le-ta je odvisna od višine telesa nad obzorjem: niže ko je telo nad obzorjem, bolj debela je plast ozračja, skozi katero potuje svetloba do teleskopa, zato se je več absorbira in siplje. Ker sta opazovano telo in standardna zvezda običajno na različni višini nad obzorjem, je ekstinkcija njune svetlobe različno močna. Težavo rešimo tako, da oba instrumentalna sija pretvorimo v sij nad ozračjem. Za to moramo poznati višino nad obzorjem v trenutku opazovanja ter povprečno ekstinkcijo ozračja nad našim observatorijem kot funkcijo valovne dolžine.

Ko imamo izračunan instrumentalni sij zvezd nad ozračjem, je postopek naslednji. Instrumentalni sij standardne zvezde primerjamo s sijem zvezde, podan v katalogu. Razlika sijev nam da ničelni sij. Tega prištejemo instrumentalnemu siju našega telesa in tako dobimo njegov navidezni sij.

Oznake filtrov so raznolike, kot je različen nabor filtrov. Dober pregled filtrov na številnih teleskopih in instrumentih je zbran tukaj ↵
Spektralna gostota toka je količina, ki pove, koliko energije prenaša svetloba na enoto površine pri neki valovni dolžini, ali ekvivalentno, frekvenci. ↵
Dandanes obstajajo katalogi, v katerih najdemo vrednosti sija relativno svetlih zvezd (skoraj) celotnega neba. ↵

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Uvod v astronomska opazovanja za dijake in dijakinje Copyright © 2025 by University of Nova Gorica Press is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.